by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Gottlob Frege, Entry Directory]
[The following is summary. All boldface, underlying and bracketed commentary are my own.]
Summary of
Gottlob Frege
“On Concept and Object”
Brief Summary:
Frege makes a tricky but important distinction between concept and object. First note that to express a complete thought, we need a subject and a predicate. These two parts of the sentence are connected by an “is”, which can serve for two different sentence structures (that is, for two different subject-predicate relations): 1) the “copulative” predicating “is”, by which the predicate serves to predicate the subject, as for example when a property is predicated to an object, and 2) the equative “is”, by which the predicate and the subject are taken as equaling one another, similar to how the equals sign operates in a mathematical equality formula (in this case, the predicate could, grammatically speaking, be said to be a predicate nominative). Regarding predicative statements (that is, the first kind), the subject can be either an object or another concept. But it cannot be both. It is an object if it is a name. But it is a concept if within it is again a subject-predicate relation. Consider the example, “the square root of 4 has a value”. In the sentence as a whole, the predicate is “has a value”, and “the square root of 4” is the subject. But the subject here is a concept and not a name. It thus has an implied subject-predicate structure: the subject is “the value in question (in fact, 2 or –2)”, and the predicate is “is the square root of 4”. Also note that the predicate is conceptual in nature. Thus the original sentence as a whole has a concept-concept relation, and the subject of the original sentence itself has an object-concept relation. Frege has a similar and related distinction between “marks” and “properties”. A mark is something like a name that expresses properties (which can be held by some other object or concept). But a mark is not itself a property. Also, a property is to be understood conceptually, as with predication being conceptual. So suppose you have some thing t that has the properties x, y, and z. The object t is said to “fall under” the concepts x, y, and z. We can combine all three properties x, y, and z into one phrase a. In this case, x, y, and z are marks of a. But they are properties of t. This illustrates Frege’s point that something can be both a mark and a property (as x, y, and z are in the example), but something cannot be the mark and the property of the same thing (x, y, and z are marks of a but properties of t). This is related to and coherent with Frege’s more central point that something cannot at the same time be both a concept and an object. (These roles can switch only by reformulating the sentence itself). For, there is an absolute distinction between the two.
Summary
Frege is replying to Benno Kerry’s comments on Frege’s Grundlagen der Arithmetik and other works. Frege politely notes at the beginning that Kerry misunderstood the way Frege uses the concept of ‘notion’, and Frege will now take this as an opportunity to clarify and develop his thinking on the matter.
In a series of articles in this Quarterly on intuition and its psychical elaboration, Benno Kerry has several times referred to my Grundlagen der Arithmetik and other works of mine, sometimes agreeing and sometimes disagreeing with me. I cannot but be pleased at this, and I think the best way I can show my appreciation is to take up the discussion of the points he contests. This seems to me all the more necessary, because his opposition is at least partly based on a misunderstanding, which might be shared by others, of what I say about the concept; and because, even apart from this special occasion, the matter is important and difficult enough for a more thorough treatment than seemed to me suitable in my Grundlagen.
(42)
Frege clarifies that he was using the term ‘concept’ strictly in its logical sense and not in its psychological sense.
Kerry’s misunderstanding stems from him confusing his own usage of ‘concept’ with Frege’s. (42)
Kerry challenges Frege’s “definition” of concept, but Frege never gave such a definition. This is because he considers the concept to be logically simple, meaning that it cannot be decomposed into smaller units, and thus it cannot be defined.
Kerry contests what he calls my definition of' ‘concept.’ I would remark, in the first place, that my explanation is not meant as a proper definition. One cannot require that everything shall be defined, any more than one can require that a chemist shall decompose every substance. What is simple cannot be | decomposed, and what is logically simple cannot have a proper definition. Now something logically simple is no more given us at the outset than most of the chemical elements are; it is reached only by means of scientific work. If something has been discovered that is simple, or at least must count as simple for the time being, we shall have to coin a term for it, since language will not originally contain an expression that exactly answers. On the introduction of a name for something logically simple, a definition is not possible; there is nothing for it but to lead the reader or hearer, by means of hints, to understand the words as is intended.
(42-43)
Frege quotes Kerry where he indicates that the distinction between concept and object is not absolute. In the quotation, Kerry explains that “the properties of being a concept and of being an object” are not “mutually exclusive,” and he gives an example. [At this point, it seems Kerry is making the following point. On the one hand, he wants to make a conceptual and terminological distinction between what he calls the ‘concept’ and the ‘concept-object’. He says that even though they can be distinguished, that on the other hand does not mean they cannot also overlap in some cases. To conclude that ‘because they are distinct they cannot overlap’ is to make a mistaken inference. An analogous mistaken inference, he offers as illustration, is to say that because someone is a father means that they cannot also be a son (to another man who is their father). In this illustration, we see that the concepts of “father” and “son” can overlap, just as the concepts of “concept” and “concept-object” can overlap (in some cases).]
Kerry wants to make out that the distinction between concept and object is not absolute. ‘In a previous passage,’ he says, ‘I have myself expressed the opinion that the relation between the content of the concept and the concept-object is, in a certain respect, a peculiar and irreducible one; but this was in no way bound up with the view that the properties of being a concept and of being an object are mutually exclusive. The latter view no more follows from the former than it would follow, if, e.g., the relation of father and son were one that could not be further reduced, that a man could not be at once a father and a son (though of course not, e.g., father of the man whose son he was).’
(43)
Frege now clarifies that the concept for him is predicative, but names of objects, that is, proper names, cannot serve as grammatical predicates. But here we need to clarify, because one can object that “...is Alexander the Great” can be a predicate which is also a proper name. To explain the difference, Frege distinguishes two uses of the word ‘is’: 1) as a copula acting as a verbal sign of predication, for example ‘this thing is green’ or ‘this thing is a mammal’. In such cases, we can think of this predication as an adjectival modification on the grammatical subject: ‘this green thing’, this mammalian thing’.
We are here saying that something falls under a concept, and the grammatical predicate stands for this concept.
(44)
2) The other use of ‘is’ is like the equals sign in math, which expresses an equation, for example ‘this thing is Alexander the Great’, ‘it is the number four’, or ‘it is the planet Venus’. When we equate two names, we have two terms for the same thing. But when we predicate a grammatical subject, we are assigning the concept of that thing to the name for that thing. One important difference is that the equation formulation is reversible, but the predication one is not.
In the sentence ‘The morning star is Venus,’ we have two proper names, ‘morning star’ and ‘Venus,’ for the same object. In the sentence ‘the morning star is a planet’ we have a proper name, ‘the morning star,’ and a concept-word, ‘planet.’ So far as language goes, no more has happened than that ‘Venus’ has been replaced by ‘a planet’; but really the relation has become wholly different. An equation is reversible; an object’s falling under a concept is an irreversible relation. In the sentence ‘the morning star is Venus,’ ‘is’ is obviously not the mere copula; its content is an essential part of the predicate, so that the word ‘Venus’ does not constitute the whole of the predicate. (44)
Let us restate a bit. So in “the morning star is Venus” we have two proper names, “morning star” and “Venus”, and they are connected by an equative “is”. However, if instead we have “the morning star is a planet”, we no longer are using the equative is. This is because we are no longer saying that the two names in the sentence refer to the same object. Rather, we are saying that some object falls under some concept. Frege says that the equative formulations are reversible (we can also say “Venus is the morning star”), but the predicative copula formulations are not reversible (we cannot say, “a planet is the morning star”). [I might have the next idea wrong, so consult the quotation to follow. It seems Frege then says that we can turn “the morning star is Venus” from an equation to a predication by making this addition, “the morning star is no other than Venus”. Here we are not merely saying that both “the morning star” and “Venus” refer to the same object. There is somehow now some conceptual content to it. I am not sure what. Perhaps it is something like “has the property of being identical to something that may not have been initially apparent, namely, that is it identically the same as Venus.” That is just a wild guess.]
One might say instead: ‘the morning star is no other than Venus’; what was previously implicit in the single word ‘is’ is here set forth in four separate words, and in ‘is no other than’ the word ‘is’ now really is the mere copula. What is predicated here is thus not Venus but no other than Venus. These words stand for a concept; admittedly only one object falls under this, but such a concept must still always be distinguished from the object. (44)
[Frege’s next point seems to be to explain how all of this relates to his disagreement with Kerry. So again, “is no other than Venus” is a predicate and thus stands for a concept and not for an object. However, there is a term used in this predicate, “Venus”. It can stand for an object but not for a concept. So Frege seems to be making an absolute distinction between concept and object. One cannot overlap with the other. Kerry, recall, thinks that they are not entirely “mutually exclusive.” Frege thinks they are.]
We have here a word ‘Venus’ that can never be a proper predicate, p. 195] although it can form part of a predicate. The reference of this word is thus something that can never occur as a concept, but only as an object. Kerry, too, would probably not wish to dispute that there is something of this kind. But this would mean admitting a distinction, which it is very important to recognize, between what can occur only as an object, and everything else. And this distinction would not be effaced even if it were true, as Kerry thinks it is, that there are concepts that can also be objects.
(44)
Frege then acknowledges instances that in fact support Kerry’s view [that a concept and an object can overlap]. For example, one concept might fall under a higher concept [and thus it becomes a question whether or not that concept falling under the higher one is an object, a concept, both, or to be understood some other way]. However, Kerry does not appeal to such cases as these. Instead, Kerry gives the example: ‘the concept “horse” is a concept easily attained’. [Kerry’s point seems to be that here the first part of the sentence is both a concept in its own right and as well it is something falling under another concept, and for that reason, it is both an object and a concept in the same sentence. Frege’s point will be that this is not so, but since he explains his reasoning later, I will just quote this part for now. Frege then notes that because we use the definite article in ‘the concept “horse”’, this automatically makes it strictly an object, and because we use the indefinite article in “a concept easily attained”, that means we automatically mean it as a concept.]
There are, indeed, cases that seem to support his view. I myself have indicated (in Grundlagen, §53, ad fin.) that a concept may fall under a higher concept – which, however, must not be confused with one concept’s being subordinate to another. Kerry does not appeal to this; instead, he gives the following example: ‘the concept “horse” is a concept easily attained,’ and thinks that the concept ‘horse’ is an object, in fact one of the objects that fall under the concept ‘concept easily attained.’ Quite so; the three words ‘the concept “horse” ’ do designate an object, but on that very account they do not designate a concept, as I am using the word. This is in full accord with the criterion I gave – that the singular definite article always indicates an object, whereas the indefinite article accompanies a concept-word.
(45)
Frege then notes that Kerry says we cannot base our logical rules on linguistic distinctions, but Frege says that is inevitable anyway. [I do not get that point. Perhaps Frege is using the linguistic properties of the way words and sentences are conventionally formed and used to establish logical structures, but really, according to Kerry, he should think more formally about the structures first.] Frege says that the logical distinctions in German that he finds are real distinctions. He then discusses how universally his definite/indefinite article rule applies in German. The exceptions do not ruin the validity of the rule, he argues (45-46).
Recall that Frege is saying for Kerry’s example that “the concept “horse” ’ is really an object and not a concept. But this is odd, because we are literally saying it is a concept. Yet this is why we use scare quotes or italics, namely, to clarify that we are calling something a concept but we are using it as an object. He then seems to say that when in philosophy we want to say something about a concept, we make it the subject of the sentence, and then say something about it in the predicate. Because the subject part of the sentence is where we mention the concept, we might think that this is where the concept is found. But really, this is where the object is found, and the concept is found in the predicate (46). So before mentioning the concept by name in the subject, we often first say “the concept ...”, as in:
“The concept man is empty”.
The first three words, “The concept man” are a proper name [and not a concept, despite what the name literally says]. We know this, because it cannot be used predicatively, just as “Berlin” in “Berlin is a city” cannot be used predicatively (47). [His next point I do not understand. We first consider the sentence: “Jesus falls under the concept man”. I am not sure, but his point might be that even here “the concept man”, even though it is found in the predicate, is not a concept. (It is rather just a name in the predicate.) This is because, “is a man” is the real concept. Let me quote for your interpretation.]
When we say ‘Jesus falls under the concept man,’ then, setting aside the copula, the predicate is :
‘someone falling under the concept man’ and this means the same as :
‘a man.’
But the phrase ‘the concept man’ is only part of this predicate.
(47)
[The next point seems to be that there is an objection that in cases like “all mammals have red blood”, the subject is somehow a concept. I suppose the reason for this is “mammals” is not being used as a name but rather as a concept, since we are speaking of things that are mammals (and to qualify as such is not a matter of naming them but rather falling under a concept). So in other words, the sentence “all mammals have red blood” could instead say “all things that are mammals are things that have red blood”. Another thing we could note here is how Agler (Intro section 6.5.2) explains how we formulate similar sentences in predicate logic. For example, “Every zombie is happy” would be written, (∀x)(Zx→Hx). So in this case we see that it has the same structure as the one Frege gives for “all mammals have red blood,” namely, “if anything is a mammal, then it has red blood.”]
Somebody might urge, as against the predicative nature of the concept, that nevertheless we speak of a subject-concept. But even in such cases, e.g. in the sentence
‘all mammals have red blood’
we cannot fail to recognize the predicative nature of the concept; for we could say instead: p. 198]
‘whatever is a mammal has red blood’
or:
‘if anything is a mammal, then it has red blood.’
(47)
Frege then explains that in his prior work Foundations of Arithmetic, he did not make the sense-reference distinction. And he had one name for two concepts. What he called “a possible content of judgment” is a combination of concepts he now distinguishes, namely, “thought” and “truth-value”. So he no longer approves the wording he used there. But his position is the same, namely, “taking ‘subject’ and ‘predicate’ in the linguistic sense: A | concept is the reference of a predicate; an object is something that can never be the whole reference of the predicate, but can be the reference of a subject” (47-48). [Frege’s next point is a remark, and I do not grasp it properly. His main point will be that quantifiers are not to be associated with the concept words that come right after them. Rather, they should be considered more a part of the predication, as they indicate a certain kind of relation between the subject and the predicate. His way of explaining why this is so is a little confusing. But I think his reasoning can be summarized as the following. The negation word “not” always belongs in a sentence formulation in the predication, when we negate the sentence properly. So when we are dealing with a sentence formulation in the language of predicate logic, we negate the sentence by placing the negation word “not” with the predicate itself. This means that whatever we find next to the negation word “not” in the sentence should be considered as being a part of the predicate, at least whenever we have properly negated that sentence formulation. Therefore, since in sentences with quantifiers like “all mammals are land-dwellers” we negate it by putting the “not” next to the “all” to get “not all mammals are land-dwellers”, that means the “all” quantifier properly should be considered a part of the predication rather than a part of the subject term “mammal”, which comes after “all”. Let me quote, as I am not entirely confident in my understanding of these passages.]
It must here be remarked that the words ‘all,’ ‘any,’ ‘no,’ ‘some,’ are prefixed to concept-words. In universal and particular affirmative and negative sentences, we are expressing relations between concepts; we use these words to indicate the special kind of relation. They are thus, logically speaking, not to be more closely associated with the concept-words that follow them, but are to be related to the sentence as a whole. It is easy to see this in the case of negation. If in the sentence
‘all mammals are land-dwellers’
the phrase ‘all mammals’ expressed the logical subject of the predicate are land- dwellers, then in order to negate the whole sentence we should have to negate the predicate: ‘are not land-dwellers.’ Instead, we must put the ‘not’ in front of ‘all’; from which it follows that ‘all’ logically belongs with the predicate. On the other hand, we do negate the sentence ‘The concept mammal is subordinate to the concept land-dweller' by negating the predicate: ‘is not subordinate to the concept land-dweller.’
(48)
Frege says that Kerry’s objections fail to hold when we use Frege’s notion that phrases like “the concept F” do not designate concepts but rather objects (48).
Frege then concludes that “Kerry does not succeed in filling the gap between concept and object” (48). [The idea there seems to be that Kerry never addresses the distinction that Frege so clearly presents, and so Kerry has not successfully shown that there is no such sharp and absolute distinction.] Frege then acknowledges that in his own writings he uses terms in ways which suggest a dual status for concepts and objects. [It seems that he addresses each of these examples later (except maybe the one about existence), so I just quote them now.] “I have said that to assign a number involves an assertion about a concept; I speak of properties asserted of a concept, and I allow that a concept may fall under a higher one. I have called existence a property of a | concept” (48-49). Frege will clarify what he means in these cases by giving an example. We are to compare these two sentences: “there is at least one square root of 4” and “the concept square root of 4 is realized”. His point with this example is that “a thought can be split up in many ways, so that now one thing, now another, appears as subject or predicate.” [At this point it might not be obvious what he means, but he explains himself more in what follows. For now, perhaps we can say that we have one thought about there being values for the square root of 4, namely, 2 or –2. We can express this thought in such a way that our grammatical predicate is either “is the square root of 4” or “is realized”. Frege also might be saying that as a thought in our mind, somehow prior to our linguistic expressions of that concept, it already has a fixed subject-predicate structure, which can be either different from or the same as the grammatical structure of the linguistic expression we use, but I am not sure. I quote:]
In the sentence ‘there is at least one square root of 4,’ we have an assertion, not about (say) the definite number 2, nor about -2, but about a concept, square root of 4; viz. that it is not empty. But if I express the same thought thus: ‘The concept square root of 4 is realized,’ then the first six words form the proper name of an object, and it is about this object that something is asserted. But notice carefully that what is asserted here is not the same thing as was asserted about the concept. This will be surprising only to somebody who fails to see that a thought can be split up in many ways, so that now one thing, now another, appears as subject or predicate.
(49)
His next point is that “different sentences may express the same thought” and he illustrates this by comparing the above two sentence formulations with a new one, “The number 4 has the property that there is something of which it is the square” (49). In order to determine the subject of our judgment, it matters what precise wording we use. [So in this new sentence, we have made a new subject, namely, the number 4, and we are saying that it is the square of some number.]
One thought can have many sentences expressing it, and in fact the subject and predicate of one such sentence can be switched in another, as in cases of changing a sentence from an active to a passive form. In fact, one thought could be expressed as either a singular, particular, or universal judgment. Thus as well, “It need not then surprise us that the same sentence may be conceived as an assertion about a concept and also as an assertion about an object; only we must observe that what is asserted is different” (49). [At this point, let me suggest another way to understand what Frege is saying. We have these things: 1) The predicate, which is conceptual. 2) The subject, which can be either an object or a concept. And, the subject is that which is being predicated in the sentence. 3) Objects, which are like names or specific things. And 4) concepts, which in one way or another involve predications, and they can be found either as subjects or as predicates. The main point Frege is making is that an object can never at the same time be a concept and vice versa. However, either a concept or an object can be the subject that is being predicated. This depends on the wording which renders the thought in one or in another way.] Frege gives an example. Take again the sentence, “there is at least one square root of 4”. What happens to the sentence if we change it to, “there is at least one concept of square root of 4”? We see that the assertion works when it applies to the concept square root of 4, but it does not apply to the object “the concept square root of 4.” [It seems that Frege here is giving an example for the problematic case of a concept falling under a higher concept. The problem of course is that we might then say that the lower concept is both object and concept. In the sentence, “there is at least one square root of 4”, what we have is the concept of square root of 4 falling under the higher concept of not being an empty concept. Frege’s point seems to be that in this case, we have two concepts, and not a concept and an object. So not all subject-predicate forms are thereby object-concept forms. Rather, some are concept-concept forms.]
Language has means of presenting now one, now another, part p. 200] of the thought as the subject; one of the most familiar is the distinction of active and passive forms. It is thus not impossible that one way of analysing a given thought should make it appear as a singular judgment; another, as a particular judgment; and a third, as a universal judgment. It need not then surprise us that the same sentence may be conceived as an assertion about a concept and also as an assertion about an object; only we must observe that what is asserted is different. In the sentence ‘there is at least one square root of 4’ it is impossible to replace the words ‘square root of 4’ by ‘the concept square root of 4’; i.e. the assertion that suits the concept does not suit the object. Although our sentence does not present the concept as a subject, it asserts something about it; it can be regarded as expressing the fact that a concept falls under a higher one.
(49)
Frege continues that although a concept can be predicated by another concept, that does not mean we are to consider the lower-level concept both as object and concept. [It is merely a concept.] [I am a little uncertain of how he continues explaining this. Let us look at it. He says that the sentence “there is at least one square root of 4” still presents the predicative nature of the concept. As I understand, the concept in question is “the square root of 4”. It is somehow predicative. So if we had to state directly what is the subject and what is the predicate of this concept, I wonder if it would be like the following. The subject is “the value in question (2 or –2, in fact)” and the predicate is “is the square root of 4”. But I am not sure. I say this, because Frege goes on to say that we can restate this sentence as: “There is something that has the property of giving the result 4 when multiplied by itself.” So in Frege’s account here, we have a subject- predicate structure where the subject itself has a nested subject-predicate structure. The full form is a concept-concept relation of predication. And the nested structure is an object-concept relation of predication. Let us look at this with a diagram. Let us take as our sentence, “The square root of 4 has a value.”

It has a subject-predicate structure.

The predicate is “has a value”.

The subject is “the square root of 4”.

The predicate “has a value” is conceptual.

And “the square root of 4” is a concept.

But since “the square root of 4” is a concept, that means it also has a subject-predicate form.

The predicate is “is a square root of 4”.

And the subject perhaps is “the value in question (2 or –2, in fact)”.

The predicate here as always is conceptual.

But in this case, unlike the prior one, the subject is not a concept, but rather it is an object. So we do not continue dividing it into subject and predicate.

]
But this does not in any way efface the distinction between object and concept. We see to | begin with that in the sentence ‘there is at least one square root of 4’ the predicative nature of the concept is not belied; we could say ‘there is something that has the property of giving the result 4 when multiplied by itself.’ Hence what is here asserted about a concept can never be asserted about an object; for a proper name can never be a predicative expression, though it can be part of one.
(49-50)
[So recall his example where we were not able to assert the same thing about the concept square root of 4 and the object “the concept of the square root of 4.”] Frege then clarifies that if we assert something about concept, and then make that same assertion about an object [that names this concept], we are not thereby saying something false. We are merely saying something senseless. He gives an example. [I think it works out like the following. Suppose we say, “there is a man whose name is Julius Caesar.” Let us try to break it down like the prior example. We have the subject-predicate structure of: /subject/ A man whose name is Julius Caesar /predicate/ exists (currently). (Here we might say that this can be true or false. It would be false if it were formulated to mean the Julius Caesar who is now dead, for example.) This is a concept-concept structure, because the subject is itself a concept. So this subject can be put in the subject- predicate structure: /subject/ the man in question (namely, the historical Julius Caesar) /predicate/ having the name ‘Julius Caesar’. This now is an object-concept structure. So again, we have the full sentence, “there is a man whose name is Julius Caesar,” and it both has sense and it can be true or false. However, Frege gives another example to compare with this one: “there is Julius Caesar.” Frege says that this sentence is neither true nor false, but rather is senseless. I am not sure exactly why, but let us look at what he is saying. He says that what we assert about a concept cannot be asserted about an object (presumably, that is, about a proper name standing for that same concept). So perhaps he is saying that in the first case we are clearly making a statement about the existence of some person. But in the second case, we are confusing things, because it would seem we are saying something about the existence of Julius Caesar as a concept. I am not sure. His other examples seem to re-illustrate the same point. He later gives an example with Cesar that has sense but is false “Julius Caesar is realized.” But the point there might be that the only kind of objects that can be realized are ones that take the form “the concept F’. Let me quote:]
I do not want to say it is false to assert about an object what is asserted here about a concept; I want to say it is impossible, senseless, to do so. The sentence ‘there is Julius Caesar’ is neither true nor false but senseless; the sentence ‘there is a man whose name is Julius Caesar’ has a sense, but here again we have a concept, as the indefinite article shows. We get the same thing in the sentence ‘there is only one Vienna.’ We must not let ourselves be deceived because language often uses the same word now as a proper name, now as a concept-word; in our example, the numeral indicates that we have the latter; ‘Vienna’ is here a concept-word, like ‘metropolis.’ Using it in this sense, we may say: ‘Trieste is no Vienna.’ If, on the other hand, we substitute p. 2o1] ‘Julius Caesar’ for the proper name formed by the first six words of the sentence ‘the concept square root of 4 is realized,’ we get a sentence that has a sense but is false; for the assertion that something is realized (as the word is being taken here) can be truly made only about a quite special kind of objects, viz. such as can be designated by proper names of the form ‘the concept F.’ Thus the words ‘the concept square root of 4’ have an essentially different behaviour, as regards possible substitutions, from the words ‘square root of 4’ in our original sentence; i.e. the reference of the two phrases is essentially different.
(50)
Frege then says that although these are just a small number of examples, they illustrate a principle that holds more generally. Then he summarizes his main ideas from before, so let me quote them:
the behaviour of the concept is essentially predicative, even where something is being asserted about it; consequently it can be replaced there only by another concept, never by an object. Thus the assertion that is made about a concept does not suit an object. Second-level concepts, which concepts fall under, are essentially different from first-level concepts, which objects fall under. The relation of an object to a first-level concept that it falls under is different from the (admittedly similar) relation of a first-level to a second-level concept. (To do justice at once | to the distinction and to the similarity, we might perhaps say: An object falls under a first-level concept; a concept falls within a second-level concept.) The distinction of concept and object thus still holds, with all its sharpness.
(50-51)
Elsewhere Frege discussed his ideas of “property” and “mark”, and these concepts are coherently related to what he is saying now about concepts and objects. Regarding property, we can make a formulation like: “Φ is a property of Γ”. To use the notion of mark, we can say something like “Φ is a mark of Ω”. Frege claims that one same thing can be both a property and a mark, but it cannot be the property and the mark of one same thing. [Since Frege gives the example later, let us begin with it now, then after this discussion I will quote him in the order of his presentation. So consider these three statement: “2 is a positive number”, “2 is a whole number”, and “2 is less than 10”. Here we have three properties, and at the same time, three marks. The three properties are to be a positive number, to be a whole number, and to be less than 10. So recall Frege’s stipulation, this time I quote him: “a thing can be at once a property and a mark, but not of the same thing”. His point will be that these three properties are properties of the object 2, but they are not marks of 2. Rather, they are marks of something else, namely, of the concept positive whole number less than 10. This is evinced by the fact that this concept itself positive whole number less than 10 is not itself positive, whole, or less than 10 (because it as a concept of a number is not itself a number). So let us skip back then to his more formal presentation. We begin with a concept. Under this concept “falls” other concepts, namely, its properties. Suppose object Γ has three properties: Φ, Χ, and Ψ. It seems we next find a symbol to represent all three properties, and we here select Ω. So Ω is still a property, only it is actually three properties. Now, what about Φ, Χ, and Ψ? What are they properties of? Are they properties of Ω? No, they are not, because Ω itself does not have these properties (just like the concept 10 is not itself a whole number, etc.). Rather, they are “marks” of Ω; that is to say, they are the constituent parts falling within Ω but Ω does not fall under these properties/concepts. Frege explains that for one thing to be the property of another thing is for the second thing to fall under the first. However, although they are marks of Ω, they are nonetheless still properties. But they are properties of something different, namely, of the object Γ we began this example with. So we say that Γ falls under Φ, Χ, and Ψ, but Φ, Χ, and Ψ fall within Ω. Thus Φ, Χ, and Ψ are both properties and marks, but just not of the same thing (they are properties of Γ but marks of Ω). Frege then ties this to his notion about higher-level concepts. Φ, Χ, and Ψ are first level concepts. This part I do not understand, and I will explain why. My problem has to do mainly with the fact that he uses the term “subordinate to”, which would seem to be equivalent to “falls under”, but it cannot be, given his wording. Γ falls under its property Φ, which is a first-level concept. But Ω cannot fall under Φ. Nonetheless, Ω is subordinate to Φ. I am not sure what this subordination is. Perhaps it is merely dependence for its constitution. At any rate, Ω cannot fall under a first-level property like Φ. It could only do so to a second- level concept. With these current examples I am not sure how to illustrate that. Let us look back at the prior example, “the square root of 4 has a value”. Here we have the properties, has a value and is the square root of 4. The point here might be that the square root of 4 is both a mark and a property, but just not of the same thing. It is a property of the numbers 2 and –2. So 2 and –2 fall under the concept the square root of 4. But it is not a mark for 2 and –2. It is rather a mark for “the concept of the square root of 4”. As such, it can fall under another concept, higher-level one, namely, has a value. Probably I have this wrong, which is why I will quote for your own interpretation:]
With this there hangs together what I have said (Grundlagen, §53) about my usage of the words ‘property’ and ‘mark’; Kerry’s discussion gives me occasion to revert once more to this. The words serve to signify relations, in sentences like ‘Φ is a property of Γ’ and ‘Φ is a mark of Ω.' In my way of speaking, a thing can be at once a property and a mark, but not of the same thing. I call the concepts under which an object falls its properties; thus
‘to be Φ is a property of Γ'
is just another way of saying:
‘Γ falls under the concept of a Φ.’
If the object Γ has the properties Φ, Χ, and Ψ, I may combine them into Ω; so that it is the same thing if I say that Γ has the p. 202] property Ω, or, that Γ has the properties Φ, Χ, and Ψ. I then call Φ, Χ, and Ψ marks of the concept Ω, and, at the same time, properties of Γ. It is clear that the relations of Φ to Γ and to Ω are quite different, and that consequently different terms are required. Γ falls under the concept Φ; but Ω which is itself a concept, cannot fall under the first-level concept Φ; only to a second-level concept could it stand in a similar relation. Ω is, on the other hand, subordinate to Φ.
Let us consider an example. Instead of saying:
‘2 is a positive number’ and
‘2 is a whole number’ and
‘2 is less than 10’
we may also say ‘2 is a positive whole number less than 10.’ |
Here
to be a positive number,
to be a whole number,
to be less than 10,
appear as properties of the object 2, and also as marks of the concept
positive whole number less than 10.
This is neither positive, nor a whole number, nor less than 10. It is indeed subordinate to the concept whole number, but does not fall under it.
(51-52)
Frege then quotes Kerry, who seems to be using Frege’s notions of mark and property (52).
But according to Frege, Kerry misunderstands the distinction. In the quotation, Kerry refers to “the number 4” and “ ‘the’ number 4”. [Kerry is also quoted as writing “ ‘the’ number 4 is likewise the result of additively combining 3 and 1”] . But Frege says that whatever this distinction is, it is not his concept-object distinction. Kerry wants to say that the number 4 is a concept, and ‘the’ number 4 is a concept- object. But this is really Frege’s distinction between sense and reference (52).
Frege then wants to compare two formulations based on Kerry’s text [I will enumerate them, because Frege seems to be referring to these two sentences later by their enumeration]:
(1) “the number 4 is the result of additively combining 3 and 1” and
(2) “ ‘the’ number 4 is the result of additively combining 3 and 1”.
Frege asks, is the “is” in these cases either the predicative copula or the logical equation? (52) Frege then says we need to first remove the “the” before “result” (53a). [This is perhaps in accordance with his rule that we use the indefinite article for predicates/concepts.] Frege then says that now we can say that both “the number 4” and “ ‘the’ number 4” are objects falling under the concept result of additively combining 3 and 1. He next asks, what is the difference between these two objects? [I am not following this part so well, but it seems Frege wants to change Kerry’s manner of articulating the concepts so they fit Frege’s distinctions, while doing justice to the insight Kerry is trying to communicate. So it is possible that Frege puts this question aside, and assumes there is no difference between the two formulations. Or, in what follows, Frege shows what that difference is. I cannot tell at this point which Frege is doing.] Frege then restates what Kerry is apparently trying to say: “The number 4 has those properties, and those alone, which are marks of the concept: result of additively combining 3 and 1” (53). Frege then says we might express “the first of our two sentences” [see above enumerated sentences]: “To be a number 4 is the same as being a result of additive combination of 3 and 1” (53). In that case, Kerry probably meant to say, “ ‘The number 4 has those properties, and those alone, which are marks of the concept a number 4’. p. 204] (We need not here decide whether this is true.) The inverted commas around the definite article in the words ‘ “the” number 4’ could in that case be omitted” (53). [I am a little confused here, because the formulation with the inverted commas around the “the” is the second formulation, but Frege I thought was talking just about the first one here. So I am lost here and in fact I am as well throughout this whole discussion of Kerry’s number 4 example. Perhaps Frege’s point now is that we do not need two different sentences. Rather, we just need to make one sentence with both usages of “number 4,” but in one case we use the indefinite article and in the other we use the definite article without scare quotes. I am guessing wildly.]
Frege then addresses the proper and improper uses of the definite article in these cases. We consider the sentence, “The number 4 is none other than the result of additively combining 3 and 1” (53), and we are concerned with the “the” in front of “result”. Frege says this “the” is justified if there is such a result of this combination, and if there is no more than one such result. When these conditions are fulfilled, the phrase “the result of additively combining 3 and 1” is then understood as a proper name. [Frege then refers to “both of our sentences”. I think he again is talking about the two formulations, one with the scare quotes around “the”, enumerated by us above. His idea seems to be that we will consider if both cases use the equative ‘is’. This would mean that we could put the subjects of both sentences into an equality, because they are both equated to the same predicate. In that case, there would after all be no distinction between “the concept 4” and “ ‘the’ concept 4”, as Kerry would have it. I am not certain at all, but let me offer a possible interpretation here. Recall that these are the two sentences in question:
(1) “the number 4 is the result of additively combining 3 and 1” and
(2) “ ‘the’ number 4 is the result of additively combining 3 and 1”.
Two main things are possible: 1) the “is” is predicative, or 2) the “is” is equative. According to our criteria, since there is only one result, and thus since there is in fact a result, the “the” in “the result of additively combining 3 and 1” is properly used. Were an “a” the proper term, then this would be a predication and thus the predicative use of “is”. But since “the” is correct, this is a name and thus the “is” is instead an equative is. But that means the equative “is” is used for both sentences. That furthermore means that we can equate their subjects. In that case, there is no distinction between “the concept 4” and “ ‘the’ concept 4”. Hence, Kerry is contradicting himself.] [Because my interpretation cannot be trusted, I recommend the reader see pages 52-53. Normally I would quote it all, but perhaps that would be too much text. And it seems only to illustrate a point Frege has made other ways. Also, his point was not so obvious to me here.]
Frege says that Kerry should be allowed to use the words “concept” and “object” whatever way he chooses. But Kerry should also let Frege have the same privilege, and furthermore, to acknowledge that Frege has made a more useful distinction:
I do not at all dispute Kerry’s right to use the words ‘concept’ and ‘object’ in his own way, if only he would respect my equal right, and admit that with my use of terms I have got hold of a distinction of the highest importance.
(54)
Frege then acknowledges that he may not always be expressing the distinction in a consistent way. So he asks for some charity from the reader [Note, Graham Priest quotes this passage in his book One, p.7.]
I admit that there is a quite peculiar obstacle in the way of an understanding with my reader. By a kind of necessity of language, my expressions, taken literally, sometimes miss my thought; I mention an object, when what I intend is a concept. I fully realize that in such cases I was relying upon a reader who would be ready to meet me halfway – who does not begrudge a pinch of salt.
(54)
Frege then says that perhaps the reader will find Frege’s notion of a concept to be too “unmanageable”. Rather, they might instead prefer Kerry’s idea that something can be either a concept or an object, depending on whether or not it is falling under another concept. Frege says, however, that instead of eliminating the difficulty, it has only been shifted. [For his explanation here, we should recall Frege’s distinction between saturated and unsaturated functions from “Function and Concept”. A function is unsaturated when its argument is not specified, as when for example an empty placeholder or a variable symbol is given in the argument place. And it is saturated when some specific argument is supplied. Frege’s problem with considering something as being ambiguously or dually both a concept and an object is that we cannot understand the sense of a sentence unless the subject and predicate are linked by means of this saturation structure. But when we conceive the subject as being ambiguously or dually both a concept and object, then we have lost this saturation structure and thus as well the grounds for there to be sense in the formulation. In other words, for there to be sense, there needs to be the conceptual relation of a something falling under a predicate. There is saturation when an object falls under another concept. But there is also saturation when a concept falls under another concept. But in that case, the concept itself is thought to have this saturation structure of it being composed of some object (or concept) falling under a concept. Nowhere here is something said in the same sentence to be in one respect a concept and in another respect an object. “All mammals” is a concept falling under “have red blood”. And “all mammals” contains the object “things” falling under the concept “being a mammal”. But we do not, like Kerry does, say that something is an object insofar as it falls under a concept, and thus we do not say that “all mammals” is both an object, as it falls under “has red blood” and is also a concept, as it itself involves a predication, that is, has another thing falling under it.]
Somebody may think that this is an artificially created difficulty; that there is no need at all to take account of such an unmanageable thing as what I call a concept; that one might, like Kerry, regard an object’s falling under a concept as a relation, in which the same thing could occur now as object, now as concept. p. 205] The words ‘object’ and ‘concept’ would then serve only to indicate the different positions in the relation. This may be done; but anybody who thinks the difficulty is avoided this way is very much mistaken; it is only shifted. For not all the parts of a thought can be complete; at least one must be ‘unsaturated,’ or predicative; otherwise they would not hold together. For example, the sense of the phrase ‘the number 2’ does not hold together with that of the expression ‘the concept prime number’ without a link. We apply such a link in the sentence ‘the number 2 falls under the concept prime number’; it is contained in the words ‘falls under,’ which need to be completed in two ways-by a subject and an accusative; and only because their sense is thus ‘unsaturated’ are they capable of serving as a link. Only when they have been supplemented in this twofold respect do we get a complete sense, a thought. I say that such words or phrases stand for a | relation. We now get the same difficulty for the relation that we were trying to avoid for the concept. For the words ‘the relation of an object to the concept it falls under’ designate not a relation but an object; and the three proper names ‘the number 2,’ ‘the concept prime number,’ ‘the relation of an object to a concept it falls under,’ hold aloof from one another just as much as the first two do by themselves; however we put them together, we get no sentence. It is thus easy for us to see that the difficulty arising from the ‘unsaturatedness’ of one part of the thought can indeed be shifted, but not avoided. ‘Complete’ and ‘unsaturated’ are of course only figures of speech; but all that I wish or am able to do here is to give hints.
(54-55)
Frege concludes by suggesting we look to his work Funktion und Begriff. For, here he discusses the concept of function, which carries with it the same problem.
It may make it easier to come to an understanding if the reader compares my work Function und Begriff [sic]. For over the question what it is that is called a function in Analysis, we come up against the same obstacle; and on thorough investigation it will be found that the obstacle is essential, and founded on the nature of our language; that we cannot avoid a certain inappropriateness of linguistic expression; and that there is nothing for it but to realize this and always take it into account.
(55)
Frege, Gottlob. “On Concept and Object”. Transl. P.T. Geach. In Translations from the Philosophical Writings of Gottlob Frege. Eds. P.T. Geach and Max Black. Oxford: Basil Blackwell, 1960, second edition (1952 first edition).
.


.jpeg)























































 .
.  . (This is true simply by definition. It is a convention that we can usefully build upon, and has no deeper significance.)
. (This is true simply by definition. It is a convention that we can usefully build upon, and has no deeper significance.) and
and 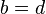 , then
, then  .
.  then
then  . Then
. Then  , so
, so  and a=c.
and a=c.  . Thus
. Thus 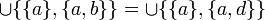 meaning
meaning  .
. , we have
, we have  and thus
and thus  so
so  , note
, note  , so
, so 














