Agler (6.6) Symbolic Logic: Syntax, Semantics, and Proof, "Mixed and Overlapping Quantifiers", summary

 

by Corry Shores

[Search Blog Here. Index-tags are found on the bottom of the left column.]

 

[Central Entry Directory]

[Logic & Semantics, Entry Directory]

[David Agler, entry directory]

[Agler’s Symbolic Logic, entry directory]

 

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

[Further note: this entry also draws from one of Agler’s class handouts,  Agler, David. “RL: Symbols, Syntax, Semantics, Translation.”

http://www.davidagler.com/teaching/logic/handouts/new/PHIL012_Handout_6.pdf ]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.6: Predicate Language, Syntax, and Semantics

6.6 Mixed and Overlapping Quantifiers

 

 

 

Brief summary:

There is no simple and universally reliable procedure for translating all English sentences with quantifiers into the language of predicate logic (RL). Agler offers four steps that can help us make translations [quoting:] {1} Identify and symbolize any English expressions that represent quantifiers (and their bound variables) and propositional operators. {2} Translate any ordinary language predicates into predicates of RL. {3} Use the quantifiers from step 1 and the predicates from step 2 and represent the proposition that (1) expresses. {4} Read the predicate logic wff in English and check to see whether it captures the meaning of the sentence undergoing translation. When we have two quantifiers and they are both the same kind, their order will not matter. However, if one is universal and the other is existential, their order can change the meaning of the proposition. Here are four scenarios that illustrate:

 

(∀x)(∃y)Lxy     “Crush scenario”

Everyone loves someone.

[For any person, that person loves one (and/or another) person.]

 

(∃y)(∀x)Lxy     “Santa Claus scenario”

Someone is loved by everyone.

[There is one (and/or another) person who is loved by all other people.]

 

(∀y)(∃x)Lxy    “Stalker scenario”

Everyone is loved by someone.

[Each person is loved by at least one (and/or another) person.

 

(∃x)(∀y)Lxy   “Loving God scenario”

Someone loves everyone.

[One (and/or another) person loves every other person.]

 

 

 

 

Summary

 

6.6 Mixed and Overlapping Quantifiers

 

Agler will provide a four-step procedure for translating English sentences into the language of predicate logic (RL) for quantifiers with overlapping scope. Such translation is an art, as there is no foolproof method. [Recall the five-step procedure from section 6.5.4.  Step 1: identify all the RL-relevant parts of the sentence and make a translation key for them. Step 2: find the main operator in the English sentence. Step 3: find the subject for each of the two propositions. Step 4: figure out what is being said about the subject in each case. Step 5: Determine the proper quantifiers and their scopes.] He begins with this example.

(1) Someone loves someone.

(Agler 277)

The first step is to identify the RL-relevant structural components to the English sentence and to symbolize “any English expressions that represent quantifiers (and their bound variables) and propositional operators” (277). In the sentence we have “Someone loves someone”. Recall from section 6.5.4 how we used the existential quantifier for instances of “someone”. We also see that we will need two variables, since “loves” is a two-place predicate. The question is, should it be the same variable in each case or a different one? Were it to be just one, then it would have said, “Someone loves themself.” But since it is one person loving another, we will need two variables and two quantifiers. But note that this still leaves it possible that some person can still love themselves. The point is that we will not make it such that there is only one person in the situation.

 

(1)	Someone loves someone.
Step 1	Identify and symbolize any English expressions that represent quantifiers (and their bound variables) and propositional operators. (Agler 277)	(∃x) and (∃y)

 

In the second step, on the basis of the translation key, we translate ordinary language predicates into the symbolic predicates of RL.

 

(1)	Someone loves someone.
Step 2	Translate any ordinary language predicates into predicates of RL. (Agler 277)	Lxy

 

For the third step we combine the quantifiers in step 1 with the predicates of step 2 in order to express the proposition we are translating.

 

(1)	Someone loves someone.
Step 3	Use the quantifiers from step 1 and the predicates from step 2 and represent the proposition that (1) expresses. (Agler 278)	(∃x)(∃y)Lxy

 

For the fourth step, we check our RL formulation by interpreting them using a bridge translation.

(∃x)(∃y)Lxy

There exists an x and there exists a y such that x loves y.

Someone loves someone.

(Agler 278)

 

(1)	Someone loves someone.
Step 4	Read the predicate logic wff in English and check to see whether it captures the meaning of the sentence undergoing translation. (Agler 278)	There exists an x and there exists a y such that x loves y.

 

Agler will now illustrate the steps with this sentence:

(2) Every zombie loves every human.

(Agler 278)

 

Step 1 tells us, “Identify and symbolize any English expressions that represent quantifiers (and their bound variables) and propositional operators.” Here we have “every” which means we will use universal quantification. But we are distinguishing things in this sentence, so there is the possibility that we will have two variables and two quantifiers. The question is, are there two totalities that we are relating in this sentence or just one? Since we are not saying zombies love themselves, there is not just one totality of things we are discussing. Instead there are two, and we are relating every member of the first totality with every member of the other totality. Thus we have two variables and two universal quantifiers.

 

(2)	Every zombie loves every human.
Step 1	Identify and symbolize any English expressions that represent quantifiers (and their bound variables) and propositional operators. (Agler 278)	(∀x) and (∀y)

 

The second step says to “Translate any ordinary language predicates into predicates of RL”. Here we have three predicates. We have things with the property of being a zombie, things with the property of being a human, and things with the property of loving other things.

(2)	Every zombie loves every human.
Step 2	Translate any ordinary language predicates into predicates of RL. (Agler 279)	Zx, Hy, Lxy

 

Step 3 is “Use the quantifiers from step 1 and the predicates from step 2 and represent the proposition that (1) expresses.” [Here it is less obvious how to do that. We might want to make a bridge sentence. We are saying something like, “suppose there are zombies and suppose there are humans, in that case, all the zombies love all the humans.” For the “suppose [something and something], in that case [something]” can take a conditional relation. So we have: “if there are things that are zombies and if there are things that are humans, then all of those zombies love all of those humans.”]

 

(2)	Every zombie loves every human.
Step 3	Use the quantifiers from step 1 and the predicates from step 2 and represent the proposition that (1) expresses. (Agler 279)	(∀x)(∀y)[(Zx∧Hy)→Lxy]

 

The fourth rule says, “Read the predicate logic wff in English and check to see whether it captures the meaning of the sentence undergoing translation.”

 

(2)	Every zombie loves every human.
Step 4	Read the predicate logic wff in English and check to see whether it captures the meaning of the sentence undergoing translation. (Agler 279)	For all x and for all y, if x is a zombie and y is a human, then x loves y.

 

Agler then gives other example sentences to help us see how the method can deliver the proper translation. [One thing we notice in the following is that when the first term is existentially quantified, we use conjunction, and when it is universally quantified, we use the conditional. Intuitively the idea seems to be that for universal quantification, we are not committing to there actually being any members of the totality in question, but rather we are saying supposing there are members, then .... And for existential quantification we of course are committing to the claim that there is such a thing being described, so we would use conjunction, on account of their existence not being a supposition. But it is still not entirely clear for me, especially in the mixed situation. So consider “some zombie loves every human.” We are affirming that there is such a zombie, and so we use conjunction.

(∃x)(∀y)((Zx∧Hy)∧Lxy)

But what if the predicate reverses this relation? What if the statement is “every human is loved by some zombie” and L means “is loved by” and Z and H have the same meanings? Do we write it

(∃x)(∀y)((Zx∧Hy)∧Lyx)

in keeping with the prior formulation, or do we write:

(∃x)(∀y)((Zx∧Hy)→Lyx)

in keeping with the idea that if the subject of the sentence is universally quantified, then we use the conditional? I would guess that we use the conditional, but I am not sure why.]

 

English Sentence	Translation into RL
Some zombie loves some human.	(∃x)(∃y)((Zx∧Hy)∧Lxy)
Some zombie loves every human.	(∃x)(∀y)((Zx∧Hy)∧Lxy)
Every zombie loves some human.	(∀x)(∃y)[(Zx∧Hy)→Lxy]
Some humans don’t love some zombie.	(∃x)(∃y)((Hx∧Zy)∧¬Lxy)
No human loves some zombie.	(∀x)(∃y)[(Hx∧Zy)→¬Lxy]

 

Agler then addresses the issue of the order of the quantifiers. If they are both universal or both existential, the order does not matter. But when we mix the quantifier types, the order can matter. [In the following I will first quote the entire section, and I will make the changes noted in another document, so that we have the proper formulations set out before us. There is one change that I can make, but the other one I cannot see how it applies to the text as I have it in my version.]

Examples like those above may give you the impression that the order of the quantifiers does not matter when you are either translating a predicate wff into English or interpreting the expression. This, however, is not the case for the following two wffs:

(∃x)(∀y)Lxy

(∀x)(∃y)Lxy

While these expressions appear similar, they express different propositions. In English, ‘(∀x)(∃y)Lxy’ expresses the proposition that Someone loves everyone. This proposition is true just in the case that there is at least one person who loves every person. In contrast, ‘(∀y)(∃x)Lxy’ expresses the proposition that Everyone loves someone. This proposition is true just in the case that every individual in the domain of discourse loves at least one person. This shows that the order in which the quantifiers are arranged has an effect on how the formula is interpreted and how we ought to translate the expression from one language into the other.

(280)

[There is a correction that says: “2nd set of formulas on page, under (∃x)(∀y)Lxy, there is (∀y)((∃x)Lxy. This should read: “(∀x)(∃y)Lxy ”. In my version, it seems I do not need to make this change, as it already had the “(∀x)(∃y)Lxy”. However, it is very possible I misunderstand how the text should be read. My main problem is that I do not see how we are discussing the order of the quantifiers. In the “mistaken” formulation, we do change the order. But in the “corrected” version, we do not change the order. Rather, we change which variable gets which quantifier (and we perhaps in addition to that change the order of the quantifiers). I still would like to know, is there a difference in meaning between:

(∃x)(∀y)Lxy

and

(∀y)(∃x)Lxy

or between

(∀x)(∃y)Lxy

and

(∃y)(∀x)Lxy

In fact, Agler has a course handout that will detail these instances. I am still unable to conceptualize what it means for one quantifier to fall under the scope of another. What I do not understand yet how one can be influenced or conditioned by the other. Vaguely it seems like we take the left-most one a sort of point of orientation, and somehow we need to combine that with the directionality of the predicate relation. Since I cannot offer any insights into it, I will quote from Agler’s handout where he goes into more detail. (In the following I insert some comments in curly brackets.)

When dealing with wffs with quantifiers whose scope overlaps, does the order of the quantifiers matter? Consider the following eight wffs (let Lxy express the two-place English expression “x loves y”)

1. (∀x)(∀y)Lxy

2. (∀y)(∀x)Lxy

3. (∃x)(∃y)Lxy

4. (∃y)(∃x)Lxy

5. (∀x)(∃y)Lxy

6. (∃y)(∀x)Lxy

7. (∀y)(∃x)Lxy

8. (∃x)(∀y)Lxy

{I am guessing that 7 and 8 should read:

7. (∀y)(∃y)Lxy

8. (∃y)(∀y)Lxy

}

While some of these wffs entail others, only the first two pairs of wffs are equivalent. That is, (∀x)(∀y)Lxy is equivalent to (∀y)(∀x)Lxy and (∃x)(∃y)Lxy is equivalent to (∃y)(∃x)Lxy. (1) and (2) express the proposition that “everyone loves everyone”. In this scenario, every item in the domain of discourse loves every item in the domain of discourse. (3) and (4) express the proposition that “someone loves someone”. In this scenario, at least one item in the discourse loves at least one other. In both cases, the order of the quantifiers does not impact the truth or falsity of the wff.

In contrast, (5)-(8) express different propositions. Let’s characterize each in terms of a scenario. (5) is what I will call the “crush” scenario. It says that everyone loves at least one person. It does not say that everyone is loved (there may be some unloved individuals). What it says instead is that for any individual in the domain of discourse, that individual will love at least one other person. In other words, everyone has a crush on someone, even though not | everyone is someone’s crush.

(6) is what I will call the “Santa Claus scenario” (I need a better name). It says that there is at least one object who is loved by everyone. This expression is similar to (5) in that it implies that everyone loves at least one person. That is, in (5), every single person loves at least one person, but the loved person can differ from person to person. For example, in a scenario consisting of Jane, John, and Sally, (5) would be true if Jane loves John and John loves Jane and Sally loves herself. In contrast, (6) is true just in the case that there is one person loved by everyone, e.g. John loves Jane, Sally loves Jane, and Jane loves Jane.

(7) is what I will call the “Stalker scenario”. It says that everyone is loved by someone. What this says is that if you go through the domain of discourse, pulling people one at a time, you will be able to find at least one other person who loves the selected person. So, if we consider Jane, John, and Sally, (7) is true in the case that, beginning with Jane, we can find at least one other person who loves Jane (e.g. John, but it could be anyone) and one person who loves John and one person who loves Sally. The person doing the loving need not be the same person in each case, nor is it the case that everyone loves someone. (7) differs from (5) in that it doesn’t imply that everyone loves at least one other person. (7), in contrast, can be true if John loves Sally and Jane and himself, but neither Sally nor Jane love anyone. (7) also differs from (6) in that it doesn’t imply that everyone loves at least one object.

(8) is what I will call the “Loving God scenario”. It says that someone loves everyone. (8) is true provided there is at least one person who loves every single person in the domain. In contrast to (5), (8) does not imply that everyone loves at least one other person. Rather, it says that there is at least one person who loves all people. In contrast to (6), (8) does not imply that there is at least one person loved by all. It only says that there is one person who loves all. Finally, while (8) implies (7)–for if someone loves everyone, then everyone is loved by at least one person–(7) does not imply (8). This is because (7) can be true in a case where (8) is not, namely in the case where everyone is loved by someone, but everyone is not loved by a single person.

1. (∀x)(∀y)Lxy Everyone loves everyone.

2. (∀y)(∀x)Lxy Everyone loves everyone.

3. (∃x)(∃y)Lxy Someone loves someone.

4. (∃y)(∃x)Lxy Someone loves someone.

5. (∀x)(∃y)Lxy Everyone loves someone.

6. (∃y)(∀x)Lxy Someone is loved by everyone.

7. (∀y)(∃y)Lxy Everyone is loved by someone.

8. (∃y)(∀y)Lxy Someone loves everyone.

{I again guess that 7 and 8 are}

7. (∀y)(∃x)Lxy Everyone is loved by someone.

8. (∃x)(∀y)Lxy Someone loves everyone.

(Agler, Handout 6)

I cannot give a good explanation for how it works when one quantifier falls under the scope of another. I have looked at other sources, and I still do not have the sort of understanding that I am looking for. I will try something, but later I hope to revise this entry so that it does a better job at explaining how this works.

 

My impression so far is that it works like the following.

 

In notes to follow, when dealing with the existential quantifier I will just think of it limiting us to one and only one member of the domain. So in the language where it reads “someone” I will just take this to mean one person, but perhaps the existential quantifier does not limit us to just one, but rather could also be some. And when I refer to “the lover” I am pointing to the x variable, and when I refer to “the beloved’,” I am pointing to the y variable.

 

Let us begin with the first two, 5 and 6.

(∃y)(∀x)Lxy

(∀x)(∃y)Lxy

In both of these, the lover is universally quantified and the beloved is existentially quantifier. This means I think that what we say about the love relation with respect to the lover will be said about each and every one of the members of the domain. What we say about the beloved will refer to one or another lover. Let us begin with

(∀x)(∃y)Lxy

Let us say in our domain there are just three members, a, b, and c. In my diagram, I will repeat the domain for both the x and y variables, for convenience of drawing the lines, but of course there is just the one domain.

The following is just my way of trying to understand how the scope works. So we have universally quantified the variable for the lover, and we have given it the greatest scope. The way I currently understand this having of greatest scope means that we begin by taking that part the relation first. It is universally quantified, so we begin by taking into consideration every member of the whole.

And, what we say about how it relates to the other variable will be something said for each member. What we say for each member is that to it is related another member of the domain. So we go through each member as lover, and we see that it is love-related to one or another member of the domain (it could also be  loving oneself presumably).

There are two important features of this structure that need clear explanation, I think. The first is that not all the members of the domain are beloveds. This is perhaps the result of the fact that we are universally quantifying the lover but only existentially quantifying the beloved. The trickier part is that it is not the same beloved that is being loved by all members (at least not necessarily so). We should try to be clear on this, because we interpret it verbally to mean “Everyone loves someone”. The bridge sentence might be, “For all x, there is a y such that x loves y.” The important question is, if we say “there is a y”, why is it not just one y to which all the other members are related? I will consider some possibilities. One is that the existential quantifier does not limit us to one member. It can also mean “some.” So in other words, we might also translate it to mean “Everyone loves someone or some people”. Another possibility might have to do not with how the quantification works but rather with how the scope works. Perhaps the idea is like this. When the universal quantifier has the greatest scope, that means we are making the relation hold for every member of the domain, but for some reason we take each one independently and take the existentially quantified variable only in the context of each lover taken on its own. In other words, we say that “a” is related to one or another beloved. Then we move to “b.” But we put aside who we said “a” is related to. “b” then we see is related to some beloved. I think the real reason must be different than these, but I cannot figure it out.

 

Now let us consider:

 

(∃y)(∀x)Lxy

This time, the existential quantifier has the greatest scope. So we begin with it.

The quantifier for the lover is universally quantified, so we know that all members of the domain are lovers to the one beloved.

With the prior case of (∀x)(∃y)Lxy, the lovers could take different beloveds. But in this case, they all must take the same one. If I am not mistaken, I think that limits the scenario to these possible situations.

 

Now let us do:

(∀y)(∃x)Lxy

and

(∃x)(∀y)Lxy

What makes this pair different is that now the beloveds are universally quantified, which means what we say of the relation will involve all members of the domain being beloveds. And the lover is existentially quantified, which means that the beloveds, one way or another, will be related to just one (or some) lovers.

Let us begin with

(∀y)(∃x)Lxy

The beloveds (the y variable) have the greatest scope, so we begin with them first. It is universally quantified, which means we will be making the relation hold for every one of them.

The lover is existentially quantified. So we know that for every beloved, there is a lover. But that does not mean for every beloved there is the same lover or that every lover has a beloved.

 

Finally, let us look at

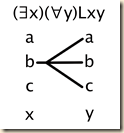
(∃x)(∀y)Lxy

The lovers here have the largest scope, and they take the existential quantifier. This means we will begin with one x.

The beloveds take the universal quantifier, which means the relation is said of all of them.

]

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.

 

Or if otherwise noted:

Agler, David. “RL: Symbols, Syntax, Semantics, Translation.”

http://www.davidagler.com/teaching/logic/handouts/new/PHIL012_Handout_6.pdf

 

Some changes to the book quotations may have been made, as based on: http://markdfisher.com/wp-content/uploads/2014/02/PHIL_012_ONLINE_SYLLABUS_SP14-3-1.pdf .

 

.