Agler (6.2) Symbolic Logic: Syntax, Semantics, and Proof, "The Language of RL", summary

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[David Agler, entry directory]
[Agler’s Symbolic Logic, entry directory]

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.6: Predicate Language, Syntax, and Semantics

6.2 The Language of RL

 

 

 

Brief summary:

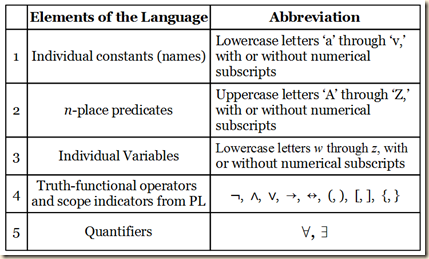
There are five elements in the language of predicate logic (RL).

1) Individual constants or names of specific items, and they are represented with lower case letters spanning from ‘a’ to ‘v’ (and expanded with subscript numerals).

2) n-place predicates, which predicate a constant or variable, or they relate constants or variables to one another. They are represented with capital letters from ‘A’ to ‘Z’ (and expanded with subscript numerals).

3) Individual variables, which can be substituted by certain constants, and they are represented with lowercase (often italicized) letters spanning from ‘w’ to ‘z’ (and expanded with subscript numerals).

4) Truth functional operators and scope indicators from the language of propositional logic (PL), namely, ¬, ∧, ∨, →, ↔, (, ), [, ], {, }.

5) Quantifiers, which indicate what portion of the set of items that can stand for a variable are to be taken into consideration in a part of a formulation. When indicating that the full portion is to be considered in some instance of a variable in a formula, we use the universal quantifier ∀. We can understand it to mean “all,” “every,” and “any.” But if we are to consider only a portion of the possible items that can substitute in for a variable, then we use the existential quantifier ∃, which can mean “some,” “at least one,” and the indefinite determiner “a.”

The purpose of the language of predicate logic is to express logical relations holding within propositions. There is the simple relation of predication to a subject, which would be a one-place predicate. There are also the relations of items within a predicate, as in “... is taller than ...”, which in this case is a two-place predicate, and so on. To say John is tall we might write Tj, and to write John is taller than Frank we could write Tjf. The number individuals that some predicate requires to make a proposition is called its adicity. And  when all the names have been removed from a predicational sentence, what remains is called an unsaturated predicate or a rheme. We might also formulate those above propositions using variables rather than constants, as in Tx and Txy. When dealing with variables, the domain of discourse D is the set of items that can be substituted for the variables in question, and this possible substitutions are called substitution instances for variables or just substitution instances. The domain is restricted if it contains only certain things and it is unrestricted if it includes all things. We may either explicitly stipulate what the domain is, which is common in formal logic, or the context of a discussion might implicitly determine the domain, and this domain can fluidly change as the discussion progresses. Also, in these cases with variables, we might further specify the quantities of the variables that we are to consider. So to say, everyone is taller than Frank we might write, (∀x)Txf. Someone is taller than Frank might be (∃x)Txf. Quantifiers have a scope in the formulation over which they apply. They operate just over the propositional contents to the immediate right of the quantifier or just over the complex propositional contents to the right of the parentheses.

 

 

Summary

 

6.2 The Language of RL

 

Agler makes the following chart displaying the elementary vocabulary of predicate logic RL.

(Agler 248)

 

 

6.2.1 Individual Constants (Names) and n-Place Predicates

 

As we noted in section 6.1, we need a language that is more expressive than that language of propositional logic (PL) by “taking internal (or subsentential) features as basic” (248). We will begin by considering sentences with such logically relevant internal structures.

1) John is tall.

2) Liz is smarter than Jane.

(Agler 248)

Let us look first at 1. “John is tall.” Here we have two important internal features. On the one hand, we have the noun phrase or name John, and on the other hand we have the predicate or verb phrase is tall (Agler 248). In the second sentence, we also have proper names, Liz and Jane. In our language of predicate logic (RL), we will use lowercase letters from ‘a’ to ‘v’ for such names or constants as these. And they can optionally take subscript numerals (248). [From the examples it seems arbitrary whether or not the letter is italicized.] Agler gives these examples:

j = John

l = Liz

d₃₂ = Jane

(Agler 248)

 

Now, in RL, a name “always refers to one and only one object” and thus there are no names that fail to refer to anything. However, many names can refer to the same object. Thus for example “ ‘John Santellano’ and ‘Mr. Santellano’ can designate the same person” (249). 

 

Consider the two predicates from above, “… is tall” and “… is smarter than…”. We would consider both predicates in RL as “predicate terms”. As we can see, the predicate term in the first case only takes one individual in order to create a sentence that expresses some proposition, for example, “John is tall”. But “… is smarter than…” requires two individuals to make a proposition, as for example,  “Liz is smarter than Jane”. The number individuals that some predicate requires to make such a proposition is called its adicity. Thus the adicity of “… is tall” is one, and the adicity of “… is smarter than…” is two (249).

 

As we noted before, we use capital letters to express predicates and relations, using any letters from A to Z. And we again may use numerical subscripts so that we can have more than 26 distinct predicates if we need. Agler gives these examples:

T = is tall

G = is green

R = is bigger than

F₄₃ = is faster than

(249)

 

We also use the same truth-functional operators as in PL. We now will examine how to translate English sentences with names and predicates into RL. Agler has us recall sentence 1: John is tall. The first step is to replace its names with blanks and to assign names with letters. So we would have:

John is tall.

____ is tall

j = John

(Agler 249)

There is only one name in this sentence, so the predicate’s adicity is 1. Now, “After all names have been removed what remains is called an unsaturated predicate or a rheme” (249). We can now assign to the unsaturated English predicate a capital letter. So in all we now have:

John is tall.

____ is tall

j = John

T = ___ is tall

(Agler 249)

Now we will finally formulate the structure. [Consider that in English the predicate normally comes after the subject. In these formulations, we put the predicate symbol before the terms that the predicate is relating or predicating.] Using our above equivalences, we would make this translation:

John is tall.

Tj

(Agler 250)

 

Let us now consider a sentence with a two-place predicate, and we will give also the equivalences and final formulation.

John is taller than Frank.

j = John

f = Frank

R = ___ is taller than ___

Rjf

(Agler 250)

[There is not yet an explicit discussion of the order, but it seems that the order of the individual variables follows the order in the English sentence. I am not sure about situations where the order is not logically important even in the English formulation, as in the case of “John stands between Liz and Jane” and “John stands between Jane and Liz”.]

 

In our natural use of English it might be awkward to use predicates that take very many individuals, we still leave it as a possibility in RL to have large adicities. “Since there is no need to put a restriction on how many objects we can relate together, what remains after all object terms have been removed is an n-place predicate, where n is the number of blanks or places where an individual constant could be inserted” (250).

 

Agler then gives an example of a three-place predicate.

John is standing between Frank and Marry.

j = John

f = Frank

m = Mary

S = __ is standing between __ and __

Sjfm

(Agler 250)

 

 

 

6.2.2 Domain of Discourse, Individual Variables, and Quantifiers

 

Agler has us consider three sentences that cannot be adequately expressed merely in PL.

(3) All men are mortal.

(4) Some zombies are hungry.

(5) Every man is happy.

(Agler)

 

Previously, as with “John is tall”, we were only predicating a property to one individual. But now in these sentences we “predicate a property to a quantity of objects” (251). So we cannot simply use the formulation structures from above. Instead, as for sentence 4, we need to express “the more indefinite proposition that some object in the universe is both a zombie and is hungry” (251).

 

For such sentences as 3-5, we will need to introduce “two new symbols and the notion of a domain of discourse” (251). [The domain of discourse is all the things we might refer to in some usage of RL. In this we can have variables which may take the value of some thing in the domain of discourse. They are called individual variables and they will be symbolized with lowercase letters from w to z, and it seems they should be italicized. (Recall that individual constants, the names like John and so on, took letters ‘a’ through ‘v’ and were not in most cases italicized.) Such individual variables are like the blanks from before.]

For convenience, let’s abbreviate the domain of discourse as D and use lowercase letters w through z, with or without subscripts, to represent individual variables. The domain of discourse D is all of the objects we want to talk about or to which we can refer. So, if our discussion is on the topic of positive integers, then we would say that the domain of discourse is just the positive integers. Or, more compactly,

D: positive integers

If our discussion is about human beings, then we would say that the domain of discourse is just those human beings who exist or have existed. That is,

D: living or dead humans

 

Individual variables are placeholders whose possible values are the individuals in the domain of discourse. Individual variables are said to range over individual particular objects in the domain in that they take these objects as their values. Thus, if our discussion is on the topic of numbers, an individual variable z is a placeholder for some number in the universe of discourse.

As placeholders, we can also use variables to indicate the adicity of a predicate. Previously we indicated this by using blanks (e.g., ____ is tall). Rather than representing a predicate as a sentence with a blank attached to it, we will fill in the blanks with the appropriate number of individual variables:

Tx = x is tall

Gx = x is green

Rxy = x is bigger than y

Bxyz = x is between y and z.

(Agler 251)

 

Agler then distinguishes two ways that we determine the domain of discourse. 1) Stipulatively: here we name the objects that are in the domain. So if “the objects to which variables and names can refer are limited to human beings”, then we would write:

D: human beings

(252)

[I am not sure, but I would also think that another stipulative way is to list the individual members of the set.] So suppose a person says, “Everyone is crazy”. Since they presumably are speaking about humans, the domain of discourse D is human beings, and thus their statement is shorthand for “Every human being is crazy” (252).

 

In normal conversation, however, we do not often explicitly stipulate our domain of discourse, and in fact it might change throughout the conversation and at times or always be very difficult to determine precisely. Instead, the domain is often determined 2) contextually, so depending on what we are saying, it might be that our domain of discourse is colors or in another case human beings living in the 1900s. And the domain can often change with the flux of contextual factors. “If you and your friends are talking about movies, then the D is movies, but the D can quickly switch to books, to mutual friends of yours who behave similarly to characters in books, and so on” (252). In our uses here of RL, we will always stipulate our domain (252).

 

Agler then notes another distinction with regard to domains. They are either restricted or unrestricted. It is restricted if the domain is limited to some set of things and does not extend to others. Suppose we are doing arithmetic. Our domain is restricted to the domain of numbers. Or if we are talking about paying taxes, our domain is restricted to humans (252). But consider instead we say “Everything is crazy”. The “everything” here supposedly means not just some types of things but in fact all things no matter what. “If I wrote, Everything is crazy, this proposition means, for all x, where x can be anything at all, x is crazy. This includes humans, animals, rocks, and numbers” (252). [The next idea complicates this point a little bit. It seems that we cannot necessarily infer that the domain is restricted merely from the meanings of the terms used. We might think that in the statement “Everyone is crazy” that we are thereby automatically dealing with a restricted domain that is limited to humans. But it seems that we can also use this statement even when stipulating that we are using an unrestricted domain. Yet if we do so, we must specify that we are dealing with a limited subset of that that unrestricted domain. Let me quote as I may have it wrong:]

Another example: suppose you were to say, Everyone is crazy, in an unrestricted domain. Here, it is implied that you are only referring to human beings. But since you are working in an unrestricted domain, it is necessary to specify this. Thus, Everyone is crazy is translated as for any x in the domain of discourse, if x is a human being, then x is crazy.

(252)

 

[As we noted before, the domain limits what the variables can refer to. This means it limits what objects can be substituted for those variables. The term for those limited sets of objects is substitution instances for variables or substitution instances.]

The domain places a constraint on the possible individuals we can substitute for individual variables. We will call these substitution instances for variables, or substitution instances for short. For example, discussing the mathematical equation ‘x + 5 = 7,’ the domain consists of integers and not shoes, ships, or people. If someone were to say that a possible substitution instance for x is ‘that patch of green over there,’ we would find this extremely strange because the only objects being considered as substitution instances are integers and not patches of green. Likewise, if someone were to say, ‘Everyone has to pay taxes,’ and someone else responded, ‘My cat does not pay taxes,’ we would take this to be strange because the only objects being considered as substitution instances are people and not animals or numbers or patches of green. Thus, it is important to note that the domain places a limitation on what can be a instance of a variable.

(Agler 252)

 

Agler will now examine the quantifiers. There are two in RL.

1)  Universal quantifier: ∀. In English, “all,” “every,” and “any.”

2)  Existential quantifier: ∃. In English, “some,” “at least one,” and the indefinite determiner “a.”

(Agler 252-253, not exact quotation)

 

Let us consider the first case with the example sentence:

6)  Everyone is mortal.

[Here our predicate is: ... is mortal. And the “everyone” should be reinterpreted in terms of a quantifier and a variable.] We could reexpress 6 in a number of ways:

6a)   For every x, x is mortal.

6b)   All x’s are mortal.

6c)   For any x, x is mortal.

6d)   Every x is mortal.

Let us stick with the first formulation, but we will use parentheses [for some reason, perhaps to clarify the different parts of the formulation, namely, the quantification part and the predication part.]

6*)  (For every x)(x is mortal)

(Agler 253)

Now let us say that

Mx = x is mortal

[We now have something like:

(For every x)Mx

]

We will replace the for every x with the symbol for universal quantification to get:

6_RL)   (∀x)Mx

 

Now let us look instead at existential quantification with the following example sentence:

7)  Someone is happy.

[Here our predicate is: “... is happy”.] We could express it also as:

7a)  For some x, x is happy.

7b)  Some x’s are happy.

7c)  For at least one x, x is happy.

7d)  There is an x that is happy.

(Agler 253)

These would be equivalent to:

7*)   (For at least one x)(x is happy)

Hx will stand for x is happy. [So we now have something like:

(For at least one x)Hx

] We will replace for at least one x with the existential quantifier to get:

7_RL)   (∃x)Hx

(Agler 253)

 

 

 

6.2.3 Parentheses and Scope of Quantifiers

 

Recall from PL how we used parentheses to remove potential ambiguities regarding how to group the propositional letters that are related or modified by operators in complex expressions. For example, without parentheses, in the formula A∨B∧C we do not know if its nesting structure is (A∨B)∧C or A∨(B∧C). This is essential, as the two different groupings have different logical properties. Thus A∨B∧C is not a well-formed formula in PL. In RL, parentheses also have this same disambiguating function. But they have another function as well. They are also used to indicate the range or scope of the quantifier (254). [Note, Suppes discusses these topics in section 3.5 of his Introduction to Logic.]

 

Agler states how we are to understand the scope of the quantifier in the following way:

The ‘∀’ and ‘∃’ quantifiers operate over the propositional contents to the immediate right of the quantifier or over the complex propositional contents to the right of the parentheses.

(Agler 254)

He has us consider these examples:

1)   (∃x)Fx

2)   ¬(∃x)(Fx∧Mx)

3)   ¬(∀x)Fx∧(∃y)Ry

4)   (∃x)(∀y)(Rx↔My)

(Agler 254)

 

Let us begin with the first one:

1)   (∃x)Fx

There is only one thing to the right of the quantifier, so it ranges over Fx. What about the second one?

2)   ¬(∃x)(Fx∧Mx)

Here there is a formulation within parentheses, and there is only one such enclosed formula. So since the quantifier in these cases ranges “over the complex propositional contents to the right of the parentheses”, it would for sentence 2 range over (Fx∧Mx). Now let us consider sentence 3.

3)   ¬(∀x)Fx∧(∃y)Ry

(Agler 254)

Here we have two quantifiers. The ∀x does not range over both constituent propositions, because they are not both enclosed in parentheses. It only ranges over the formula to its right and thus only to Fx. For the same reason, the ∃y only ranges over Ry. Now what about the fourth sentence?

4)   (∃x)(∀y)(Rx↔My)

[We might want to say here that the ∃x applies to just (Rx↔My), but for reasons that we may perhaps learn later, it somehow also applies to the other quantifier too.] Here, the ∃x operates on (∀y)(Rx↔My), [because that is what is to its right.] But ∀y only operates on Rx↔My.

 

Agler now shows why scope becomes important when translating English sentences in RL and vice versa. We consider the following equivalences:

Ix = x is intelligent

Ax = x is an alien

(Agler 254)

Let us now see two similar ways to apply quantification to a conjunction of these formulations.

5)   (∃x)(Ix)∧(∃x)(Ax)

6)   (∃x)(Ix∧Ax)

(Agler 254)

At first glance, we might want to say that their meanings are identical. However, “they express different propositions and are true and false under different conditions” (254). The main idea is that in sentence 5, there could be two things, with one being intelligent and the other being an alien. This is because the quantifier only ranges over the formula to its right and does not apply to both. However, proposition 6 means that there is just one thing (or some group of things treated dually in each sub-proposition) that is both intelligent and an alien. Also these formulations are not true and are not false under the same conditions, and hence they are not logically equivalent. Thus, “Proposition (5) will be true, for example, if a stupid alien exists and some intelligent dolphin exists” (254). However, that situation does not make sentence 6 true, because it would need that the predicates apply to the same creature(s). So if the situation is that there is a stupid alien but an intelligent dolphin, 5 is true but 6 is false. [Yet, perhaps any situation that makes 6 true also makes 5 true, but I am not sure.]

 

Agler notes a helpful parallel between the scope of negation and the scope of quantification.

In each of the above cases, parentheses are used to determine what is within the scope of a quantifier. There is thus a parallel between how the scope of quantifiers is determined and how the scope of negation is determined. For example, the negation in ‘¬(P∧Q)’ applies to the conjunction ‘P∧Q,’ while the negation in ‘¬P∧Q’ applies only to the atomic ‘P.’ This is the same for quantifiers since (∀x) in ‘(∀x)(Px→Qx)’ applies to the conditional ‘Px→Qx,’ while (∀x) in ‘(∀x)(Px)∧(∀y)(Qy)’ applies only to ‘Px.’

(Agler 255)

 

Agler offers more examples to clarify further how scope works with quantifiers.

7)   (∃x)(Px∧Gy)∧(∀y)(Py→Gy)

Here, Px∧Gy falls under the scope of just ∃x, while Py→Gy only falls under ∀y. Now consider:

8)   (∃x)[(Mx→Gx)→(∃y)(Py)]

Under the scope of ∃x is the entire formulation [(Mx→Gx)→(∃y)(Py)]. But only Py falls under the scope of ∃y. And what about the following one?

9)   (∀z)¬(Pz∧Qz)∧(∃x)¬(Px)

Here, just ¬(Pz∧Qz) falls under the scope of ∀z and just ¬(Px) falls under the scope of ∃x.   (Agler 255)

 

 

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.