by Corry Shores
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Set Theory, entry directory]
[Wikibooks: Set Theory, entry directory]
[My commentary is in brackets.]
Summary of
Wikibooks: Set Theory
Sets
Sets and Elements
Brief summary:
A set is a collection of items, and it is understood in terms of its structures and behaviors. A set is uniquely identified by its members, meaning that whatever the set contains specifies what set it is. Notationally speaking, there are two ways to specify a set: 1) by listing its members, separated by commas and enclosed with curly braces, as in {1, 2}, or 2) by stating the conditions for membership, also within curly braces. These conditions are given by using a variable and stating the properties that variable must have to be included. All items satisfying that property are included, all others are excluded. It is written as {x|P(x)}, read, “the set including x’s such that x has property P.” For example, {x|x is a natural number} is the set of natural numbers. To state that some item x is included in set A we write, x ∈ A. And if it is not included, then, x ∉ A. Sets with the same members equal one another. Set members are also unique, so when specifying a set, it is superfluous if any members are repeated. Also, sets can be contained in other sets. There is the empty set, which contains no members. A one-member set is a singleton, and a two-member, a doubleton.
Summary
The notion of set must be understood as abstractly as possible, by which I mean we are to concern ourselves mostly with their structural elements and relations and less with the specific contents that may fill out these structures. As such, a set is defined simply as a collection of distinct elements whose order is unimportant. [In other contexts, especially Deleuzean ones, I refer to the items in sets as “terms.”] The purpose of this mathematicized formalization of sets is to determine their structural properties and behaviors.
Sets and Elements
Set: “A mathematical set is defined as an unordered collection of distinct elements.” [Since they are unordered, we can list them in any order we want, without changing the set itself. Also, the elements are understood to be “distinct”. Thus if we repeat an item, we really have not added a new item.] “That is, elements of a set can be listed in any order and elements occurring more than once are equivalent to occurring only once.” [wikibooks]
Terminology
There are two main ways to determine what set it is we are talking about, that is to say, there are two main ways to specify a set.
1) We can literally list all of its members, placing that list between curly braces (curly brackets). So consider a set containing three members, namely, the items: 1, 2, and 3. We would notate it:
It does not need to be numbers. So, “{mother, this ipod, my school, the planet Jupiter, 12} is also a set.” [wikibooks]
2) The other way we can specify a set is to state the conditions required for something to be a member of a set. This will tell us what belongs in the set and what does not. It saves us the trouble and in many cases the impracticality (even the impossibility) of listing all the members. We still use the curly braces. But this time we formulate the conditions of inclusion by using “|” (or in other cases the colon “:”) to mean “such that”. We then use a variable letter to stand for possible substitutions. So we might write:
This means, the set containing all x’s (all items) such that these items are either 1, 2, or 3. Or, we might state the conditions more generally, as in:
This specifies the set of all natural numbers. The general format for this sort of specification is:
Here, P(x) stands for some statement about the variable x [that is, some property it needs to have in order to be a member of the set.] We then define the set as all the objects that make P(x) true. [So consider the set of natural numbers. Were we to say, “2.5 is a natural number,” that would be a false statement, and thus 2.5 is not included in the set of natural numbers.”]
We then are given parenthetically an example [quoting]:
(For a concrete example, consider A = {x ∈ R : x2 = 1}. Here the property P is “x2 = 1.” Thus, A is the set of all real numbers whose square is one.). EXPLANATION: [A set may be defined by a property. For instance, the set of all planets in the solar system, the set of all even integers, the set of all polynomials with real coefficients, and so on. For a property P and an element s of a set S, we write P(s) to indicate that s has the property P. Then the notation A={s∈S :P(s)} indicates that the set A consists of all elements s of S having the property P. The colon : is commonly read as “such that,” and is also written as “|.” So {s ∈ S|P(s)} is an alternative notation for {s ∈ S : P(s)}. For a concrete example, consider A = {x ∈ R : x2 = 1}. Here the property P is “x2 = 1.” Thus, A is the set of all real numbers (x of R (i.e. 1)) whose square (1^2=1) is one.]
[wikibooks]
We might also want to refer to some item as belonging to a set [rather than beginning with a set and giving all its members.] So consider if we have a set called A, and x is a member of that set. We would write this by using a “modified epsilon” symbol:
However, if x is not a member of A, then we would write:
Characteristics of Sets
“A set is uniquely identified by its members.” [I am not entirely sure what “unique identification” is. From what follows it seems to be this. Whatever the members of a set are constitutes the identity of that set, or at least that upon which the identity is entirely based. This means that if you have two sets with exactly the same members, then in fact you do not really have two sets. You just have one which was written twice or in two different ways. So by determining the members of the set, we have not just determined what is contained in it, we have also determined its unique identity. No other set is allowed to have that identity, or in other words, no other set is allowed to have exactly the same members (and still be considered a different set). However, I am not entirely sure of this. The text continues to say that two sets A and B are equal if all members of A are in B and vice versa. Perhaps we are to understand it that there is really after all just one set with two names. Or perhaps they are in fact two different sets, and “unique identification” simply means that the contents of the set are enough to identify it, but different sets can have the same members and be identified with different letters. Nonetheless, still further on we are told that three sets that are defined using different approaches all are the same set. Let me quote:]
A set is uniquely identified by its members.
Moreover, the sets A and B are said to be equal if and only if every element of A is also an element of B, and every element of B is an element of A.
All the above expressions specify the same set even though the concept of an even prime is different from the concept of a positive square root.
[Wikibooks]
Another thing to keep in mind is that in order to specify a set, there is no need to repeat any members, so any such repetitions can be left out. [We seem to have the same reasoning here with regard to “unique identity”. It seems every term itself in the set has its own unique identity, meaning that another instance of naming it does not produce a new term with its own identity but rather only reiterates an existing one.]
Repetition of members is inconsequential in specifying a set. The expressions
{1, 2, 3}
{1, 1, 1, 1, 2, 3}
{x | x is an even prime or x is a positive square root of 4 or x = 1 or x = 2 or x = 3}all specify the same set.
[Wikibooks]
Another characteristic of sets is that they are unordered, so we can list the members in any order we wish. Thus the following expressions all specify the same sets:
Also note that sets can contain other sets. [These internal sets will have their own curly braces around them.] For example, the following specifies one set [the curly braces with the broadest scope] containing other sets inside it [the curly braces inside with smaller scopes].
Some special sets
Although all sets are uniquely indentified by their members and are normally specified with them, there are some important sets which for convenience are specified by their customary names. For example:
The set with no members is the empty or null set. The expressions
all specify the empty set.
[Wikibooks]
Also, a set with exactly one member is called a singleton, and one with exactly two members is called a doubleton. “Thus {1} is a singleton and {1, 2} is a doubleton.” [Wikibooks]
Source (of text and images):
Wikibooks. “Set Theory/Sets.” <https://en.wikibooks.org/wiki/Set_Theory>
(Accessed 25-03-2016)
.






.jpeg)









































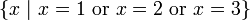

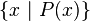

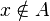

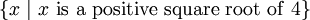
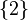






No comments:
Post a Comment