by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Graham Priest, entry directory]
[Priest’s Logic: A Very Short Introduction, entry directory]
[Bracketed commentary and boldface (unless otherwise indicated) are my own. Please forgive my typos, as proofreading is incomplete.]
Summary of
Graham Priest
Logic: A Very Short Introduction
Ch.5
Self Reference: What is this Chapter About?
Very Brief Summary:
Self-reference can present problems in logic, which leads us to conclude that there are actually four and not just the first two of the following possibilities. A sentence can be either 1) just true, 2) just false, 3) both true and false, or 4) neither true nor false. The liar sentence, “This sentence is false,” is a candidate for the third option, and its “cousin,” “This sentence is true,” for the fourth. There are certain inferences that intuitively seem valid, but under the first two “classic” assumptions they are deemed invalid. To their credit, the new assumptions make them valid. However, other inferences that the classic assumptions rightly deems valid are counter-intuitively deemed invalid under the new assumptions. There are further problems with the new assumptions. The valueless “cousin” sentence is assumed to be not true (and as well not false), but it in fact says of itself that it is true. And a stronger version of the liar sentence, “This sentence is not true,” is not just true and false but in a more problematically contradictory way it is as well both true and not-true.
Brief Summary:
Paradoxical and otherwise problematic instances of self-reference lead us to suspect that we have more options than the following two: 1) a sentence can be just true, or 2) a sentence can be just false. Consider the “liar” sentence, ‘This sentence is false.’ If it is true, then it is false; but if it is false, then it is true. Either way, it’s truth-value will contradict what it says its truth-value is. So we have option 3) a sentence can be both true and false. Or consider the “liar cousin” sentence, ‘This sentence is true.’ Normally the terms in such a declarative sentence refer to things or situations by which we may determine the truth or falsity of the statement, that is to say, whether or not the indicated situation holds in reality or not. So if we say, “this chair is red,” we look to the indicated chair and its color, and we determine if the sentence is true or not. However, the terms in “this sentence is true” does not point us to such a determining situation, since we are only able to make two equally viable assumptions about its truth value, namely, that it is either true or that it is false; but, we have no way to make the determination one way or another, since it will always be consistent with what it says of itself under both assumptions. It would seem that we have no grounds that would allow us to determine whether it is true or false, and thus we have option 4) a sentence may be neither true nor false. The classical assumptions 1 and 2 lead us to conclude certain inferences are valid when our intuitions say otherwise. For example, “The Queen is rich,” “The Queen isn’t rich,” therefore, “Pigs can fly” (q, ¬q/p). Our intuitions tell us this seems invalid. But by just using assumptions 1 and 2, it is valid, since structurally speaking there is no situation where the premises are true and the conclusion is false. For, the premises can never all be true anyway. However, under the new assumptions, particularly that sentences can be both true and false, q, ¬q/p can be valid, if q is both true and false and p just false. For, q is at least true and ¬q is also at least true. However, our intuitions tell us that q∨p, ¬q/p is valid, but the new assumptions deem it invalid. Yet, perhaps it only seems intuitively valid if we forget that there are exceptional situations where sentences can be both true and false. There are other problems with the assumptions. When we assume that the liar cousin, “This sentence is true,” is neither true nor false, that means it cannot be true, but it says of itself that it is true. And while we might go along with saying that “This sentence is false” is both true and false, we might not feel the same way about “This sentence is not-true”. Here, we might conclude that it is both true and not-true (and not just true and false), which is a stronger contradiction that we may not want to accept.
Summary
This issue of reference is not a simple one, especially in cases of self-reference. Sometimes a name refers to something larger that it is a part of. “For example, consider the sentence ‘This sentence contains five words’. The name which is the subject of this sentence, ‘this sentence’, refers to the whole sentence, of which that name is a part” (31). We also have self-reference in the following other cases. There is the name “These regulations” in the sentence, “These regulations may be revised by a majority decision of the Department of Philosophy”. [Here the larger body of regulations of which this stipulation is a part is referred to by the name “These regulations”.] And there is the name “this thought” in the thinking of the person who says “If I am thinking this thought, then I must be conscious” (31).
All these instances above are not problematic cases of self-reference. But there are ones that are. Consider:
This very sentence that I am now uttering is false.
(31d)
We will call the sentence above λ. Now we ask, is it true or false?
Well, if it is true, then what it says is the case, so λ is false. But if it is false, then, since this is exactly what it claims, it is true. In either case, λ would seem to be both true and false.
(32a)
But matters are not much better with this statement:
This very sentence that I am now uttering is true.
(32)
Why? It would seem consistent. If it is true, then it is true, since it says it is true. And if it is false, then it is false, since it claims instead to be true. But, how would its truth or falsity be determined? [The only way it seems it can be determined is by assumptions, and even this does not determine it as one or the other, because both are equally valid. Since its truth or falsity cannot be determined anyway, it perhaps has neither value.]
there would seem to be no other fact that settles the matter of what truth value it has. It’s not just that it has some value which we don’t, or even can’t, know. Rather, there would seem to be nothing that determines it as either true or false at all. It would seem to be neither true nor false.
(32)
These are ancient paradoxes. The first one, “This sentence is false” is a form of the liar paradox, which was discovered by the ancient Greek philosopher Eubulides. Liar type paradoxes also have appeared in recent debates, “some of which play a crucial role in central parts of mathematical reasoning” (32). [The next paradox involves the mathematical and logical notion of a set. Sets are abstract in a way that allows for self-reference.] One such important paradox is found in set theory, and it involves the set of all non-self-including sets. To arrive at this paradox, we need to walk through some other concepts.
A set is a collection of objects. Thus, for example, one may have the set of all people, the set of all numbers, the set of all abstract ideas.
(32)
[But as we mentioned, there is an element of abstraction to sets that allows for them to be taken as members of other sets.]
Sets can be members of other sets. Thus, for example, the set of all the people in a room is a set, and hence is a member of the set of all sets.
(32)
[Furthermore, a set can even include its very own self. To understand this, we of course cannot imagine a set as being like a physical container like a jar, because then it could not physically fit within itself. Also, there is a strange doubling that seems to be happening which could not be understood with physical metaphors. We are dealing a self-inclusive set abstractly, which means there is one set, and thus it has just one name, but it is regarded doubly, namely, as being the set that is including itself and also the set that is included in itself.]
Some sets can even be members of themselves: the set of all the objects mentioned on this page is an object mentioned on this page (I have just mentioned it), and so a member of itself; the set of all sets is a set, and so a member of itself.
(32)
Many sets, however, cannot be self-inclusive.
And some sets are certainly not members of themselves: the set | of all people is not a person, and so not a member of the set of all people.
(32-34 [The text skips page 33, which is entirely an image])
[So we have the following progression of concepts, with a new addition: 1) some simple set of things, 2) a set included in another set, as for example the sets included in the set of all sets, 3) a set that is included in itself, and thus the set to which this set belongs is not really other to it, and now, 4) a set that does not include itself, and furthermore 5) the set of all sets that do not include themselves.] So now we “consider the set of all those sets that are not members of themselves” (34). We will call this set of all non-self-inclusive sets R. We now ask, “Is R a member of itself, or is it not?” (34). [The problem will be that like the liar sentence, its status of self-inclusion is indeterminable. To write out the following more fully: If the set of all non-self-inclusive sets is included in itself, then it is not really a non-self-inclusive set, since it is self-inclusive. If the set of all non-self-inclusive sets is not included in itself, then it would belong within itself as as a member, because it is non-self-inclusive.]
If it is a member of itself, then it is one of the things that is not a member of itself, and so it is not a member of itself. If, on the other hand, it is not a member of itself, it is one of those sets that are not members of themselves, and so it is a member of itself. It would seem that R both is and is not a member of itself.
(34)
This paradox is called Russell’s paradox, named after its discoverer, Bertrand Russell. Just as we saw with liar paradox, it is also problematic to have the set of all self-inclusive sets.
Like the liar paradox, it has a cousin. What about the set of all sets that are members of themselves. Is this a member of itself, or is it not? Well, if it is, it is; and if it is not, it is not. Again, there would seem to be nothing to determine the matter either way.
(34)
[Recall what we said in Chapter 2. There we were looking at truth conditions and truth functions. On page 9 for example, Priest has us assume when making a truth table for negation “that every sentence is either true or false, but not both” (9).] These problematic examples of self-reference challenge our assumption that we made in Chapter 2 that “every sentence is either true or false, but not both. ‘This sentence is false’, and ‘R is not a member of itself’ seem to be both true and false; and their cousins seem to be neither true nor false” (34). [In section 1.3 of Priest’s In Contradiction, he explains these two situation using the terms gaps and gluts. To understand this distinction, we need to note a semantics issue. I think to follow through these ideas, we might consider a different class of statements altogether, namely, ones that refer to things other than themselves. So, “this chair is red” is true if the chair is red and false if it is not. Why is this different than “this statement is false”? We take note that the terms in “this chair is red” refer to a situation that may determine the truth value of the statement. How that truth value is determined is another matter. But the fact is, presumably, if certain basic conditions are met, that to which the terms refer can definitely determine the statement’s truth value. Now, what is it that terms in “This sentence is true” refer to? They refer back to the sentence itself. But the problem is that the sentence itself, unlike the chair’s color, cannot determine the truth value of the statement. As Priest writes in In Contradiction, “the semantic rules governing the use of the demonstrative ‘this sentence’ and those governing the predicate ‘is True’ appear not to be sufficient to determine the Truth value of the sentence” (In Contradiction 15). In this case, there is a truth-value “gap” since it can be determined neither as true nor as false. What about “This sentence is False”? Here we have the same structure of self-reference with the term “this sentence” and now we have the predication “is False”? For some reason that I do not quite grasp clearly, here the situation is different. I do not understand so well, because one could say that this second sentence is not doing anything different than the first. For the first case, the “truth-teller”, if we assume it is true then it is true and if we assume it is false it is false. In the second case, the “liar”, if we assume it is true it is false and if we assume it is false it is true. On those grounds, why do we not say that the liar also is neither true nor false, since we as well cannot on the basis of the terms determine one value or the other? This I do not understand. Perhaps the idea is the following. The truth-teller’s truth-value cannot be rightly found. It can only be endowed by means of assumption, which means that it intrinsically has no value on its own. The liar sentence always outputs the opposite of your assumptions, which contradicts what it says it should be. For the liar it does matter what your input is, because you get a self-consistent consistent output. But since the liar’s output is always inconsistent with its meaning, it does not matter what you input. For, its output can be inputted again to once more get the opposite output value. If it is true, then it is false, but if it is false, then it is true. So given this problematic circularity, it does not matter what assumption you begin with. But as you can see I am not certain what justifies us in distinguishing them fundamentally. At any rate, taking it for granted that the liar sentence is both true and false, we here have a “glut” since there is too much determination of its truth value, rather than a lack of it like in the truth-teller.]
Priest says we can accommodate this problematic situation by taking these other truth-status possibilities into account.
Assume that in any situation, every sentence is true but not false, false but not true, both true and false, or neither true nor false.
(34)
We recall the truth conditions for negation, conjunction, and disjunction from chapter 2.
In any situation:
¬a has the value T just if a has the value F.
¬a has the value F just if a has the value T.a & b has the value T just if both of a and b have the value T.
a & b has the value F just if at least one of a and b has the value F.|
a ∨ b has the value T just if at least one of a and b has the value T.
a ∨ b has the value F just if both of a and b have the value F.
(34-35)
[Instead of following the prior restriction that allowed only for true or false values,] we will “work out the truth values of sentences under the new regime” (35). [It seems here Priest is selecting as exercises three possible truth situations for negation, conjunction, and disjunction. 1) First we suppose a classical logic situation where a is false but not true. Here, negation simply flips the value. 2) Second we suppose a glut situation where a is both true and false, while b is just true, and the two are joined conjunctively. Here, the whole conjunct is both true and false. It seems the reasoning is this. Since a is at least true, that makes a & b true. But since it is also false, that makes a & b false as well. 3) Third we suppose a gap situation where a is just true, but b is neither true nor false, and the two are joined disjunctively. Here a ∨ b is merely true. The reasoning is as follows. What would make it false is only if both a and b are false. But since at least a is true, it does not matter that b is neither, and so the disjunction is always true.] [In the following, for the “clauses” (c1/c2), I insert them in curly brackets for convenience.]
• Suppose that a is F but not T. Then, since a is F, ¬a is T (by the first clause for negation).
{c1: ¬a has the value T just if a has the value F.} And since a is not T, ¬a is not F (by the second clause for negation). Hence, ¬a is T but not F.
{c2: ¬a has the value F just if a has the value T.}• Suppose that a is T and F, and that b is just T. Then both a and b are T, so a & b is T (by the first clause for conjunction).
{c1: a & b has the value T just if both of a and b have the value T.}
But, because a is F, at least one of a and b is F, so a & b is F (by the second clause for conjunction). So a & b is both T and F.
{c2: a & b has the value F just if at least one of a and b has the value F.}• Suppose that a is just T, and that b is neither T nor F. Then since a is T, at least one of a and b is T, and hence a∨b is T (by the first clause for disjunction).
{c1: a∨b has the value T just if at least one of a and b has the value T.}
But since a is not F, then it is not the case that a and b are both F. So a∨b is not F (by the second clause for disjunction). Hence, a∨b is just T.
{c2: a∨b has the value F just if both of a and b have the value F.}).
(35)
Now we wonder what this means for validity. Recall that “A valid argument is […] one where there is no situation where the premisses are true, and the conclusion is not true” (35). This is still the case, as is the fact that “a situation is […] something that gives a truth value to each relevant sentence” (35). The only difference is that situations now may also give either two truth values or none. We will now ask if the inference q/q∨p is valid. [The basic idea here seems to be that we cannot have a situation where the conclusion is not true while the premise is true. This is because we assume that q is true. That is enough to make the disjunct true, where q appears again. Thus it is valid. If q is false, then we cannot determine the validity anyway, so those cases do not matter. I wonder, what if q is both true and false? Perhaps that does not change the situation, since insofar as it is false, it has no bearing on the test for validity of the inference. I am not sure about this, but that might be what Priest is suggesting below in parentheses.]
So consider the inference q/q∨p. In any situation where q has the value T. (It may have the value F also, but no matter.) Thus, if the premiss has the value T, so does the conclusion. The inference is valid.
(35)
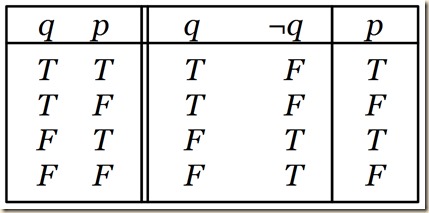
[Recall another inference from chapter 2: q, ¬q/p. We noted that we cannot have any situation where all the premises are true and the conclusion false. This is because we have both q and its negation, which means always at least one premise will be false. Because we do not even need to relate the premises to the conclusion, we called it vacuously valid. Here was the truth table:
] Under the old assumptions, q, ¬q/p is valid, but under the new ones, it is invalid. [The reasoning for this seems to be the following. q can be both true and false, and p just false. This means that ¬q is both true and false. Now since both ¬q and q are both true and false, they are both at least true, while the conclusion is false, thus making the inference invalid. Of course a concern could be that this reasoning does not work, since ¬q and q are also both false, and thus this case of glut values does not allow us to test the validity of the inference. Priest says that their additional falsity does not matter. I am not exactly sure why. It again could be the fact that even though they are no less false as true, that falsity is not relevant to the test of validity, and only their truth is relevant. I find these paraconsistency ideas absolutely fascinating philosophically. We do not take the joint truth and falsity as an unbreakable pair of values. They both stand independently on their own. Both values are absolutely affirmative in the sense that the one does not subtract from the other. I find this affirmative concept of “both” in application to truth and falsity to be quite interesting and powerful. It is addition without mixture or contamination, but the things being combined you would normally think would interfere with each other’s value.] Priest will explain why under the new assumptions q, ¬q/p is an invalid inference. [The fact that the new assumptions correspond more with our intuitions about the inference suggest that classical logic is inadequate and that we instead should consider a non-classical logic.]
just take a situation where q has the values T and F, but p has just the value F. Since q is both T and F, ¬q is also both | T and F. Hence, both premisses are T (and F as well, but that is not relevant), and the conclusion, p, is not T. This gives us another diagnosis of why we find the inference intuitively invalid. It is invalid.
(35-36)
Priest then says that “As we saw in Chapter 2, this inference follows from two other inferences,” namely, q/q∨p and
q∨p, ¬q
p
[I recall the discussion of these other inferences, but at the time I did not realize that q, ¬q/p followed from them. I am still unsure how this is, but perhaps the idea is the following. The inference q, ¬q/p seems to throw in p at the end, and to all appearances it comes out of nowhere. So it would make sense if we introduce it in the premises, hence the need for q/q∨p, which seems to justify introducing other terms. But now that there are two terms, and we infer from them merely one of the two, we need a way to eliminate one of them. Hence the q∨p, ¬q/p. Most likely the above reasoning is not what Priest means by q, ¬q/p follows from these other two inferences. Perhaps he is just saying that if you begin with these other two inferences, you can combine them to get in essence q, ¬q/p.] Priest will now find a way to invalidate q∨p, ¬q/p by finding an instance (using our new assumptions) where the premises are true and the conclusion false. So we assume that p is just false, and p is of course the conclusion. But we assume that q is both true and false. This means “that both premisses get the value T (as well as F). But the conclusion does not get the value T. Hence the inference is invalid” (36).
[Previously these new assumptions allowed us to determine q, ¬q/p as invalid, which matched our intuitions about the inference. This was one advantage over the old (classical) assumptions. But now Priest acknowledges this case where the new assumptions make q∨p, ¬q/p invalid, which goes against our intuitions. Priest will still defend the new assumptions. His basic point seems to be that really it does in fact match out intuitions, but only when we are keeping in mind instances where q can be both true and false, as in the liar paradox. Then the inference intuitively seems valid.]
In Chapter 2, I said that this inference does seem intuitively valid. So, given the new account, our intuitions about this must be wrong. One can offer an explanation of this fact, however. The inference appears to be valid because, if ¬q is true, this seems to rule out the truth of q, leaving us with p. But on the present account, the truth of ¬q does not rule out that of q. It would do so only if something could not be both true and false. When we think the inference to be valid, we are perhaps forgetting such possibilities, which can arise in unusual cases, like those which are provided by self-reference.
(36)
Priest invites us to think about which explanation (the current one or the one from chapter 2) we find more compelling. Priest then notes other problems with the new assumptions. [I do not grasp the main ideas here clearly enough to restate them properly. The main idea is that even with our new ‘gap’ and ‘glut’ assumptions, we still have unresolved problems with the liar and its cousin. Regarding gaps, Priest discusses many problems with them in his In Contradiction. See section 1.3 and section 4.7. In our current treatment here, Priest shows that we still have a contradiction with the gap assumption applied to the cousin. Even though we begin by assuming that it has neither a true nor a false value, we know from this that it is at least not true (for if it were true, then we are not using the gap assumption). However, it says of itself that it is true.]
Consider the liar paradox and its cousin. Take the latter first. The sentence ‘This sentence is true’ was supposed to be an example of something that is neither true nor false. Let us suppose that this is so. | Then, in particular, it is not true. But it, itself, says that it is true. So it must be false, contrary to our supposition that it is neither true nor false. We seem to have ended up in a contradiction.
(36-37)
Then he turns to the liar sentence, but now under a different formulation, “This sentence is not true,” which also presents a contradiction. [I think I do not adequately grasp the point here. We will conclude that the sentence results in a contradiction. I had thought that by saying it is both true and false we were already acknowledging there is a contradiction. Also, we are making a distinction between not-true and false, which I do not know how to make. I will quote it below, because I cannot convey the meaning well in my own words and thinking. He does not present it this way, but I let me offer the following formulation. We begin with “This sentence is not true”. We say it is both true and false. Insofar as it is true, what it says of itself holds, and thus it is also not true. Insofar as it is false, what it says of itself does not hold. Thus it is not the case that it is not true, therefore it is true, but it says of itself that it is not true. So we have more than just the sentence being both true and false, as per our assumptions. It is as well both true and not true, in accordance with its stated self-determinations. So the idea here might be the following. Someone could think that it is one thing to say that a sentence is both true and false. But that is not as strong and as evident a contradiction as to say that it is both true and not true. So perhaps we might be willing to go along with saying that a sentence has both the values 1 and 0, or T and F. But we might not feel so sure if we take it another step to say that it is both 1 and not 1, or T and not T. I am not sure why someone would accept the first articulation but reject the second. And as I said, I also do not know how to distinguish not-T from F. If we only have two values, I would think that they would be equivalent. Perhaps the idea is that with the new assumptions they are not equivalent. The liar cousin under the gap assumption is not T but also not F. Thus not-T and F are not equivalent there. So his point might be that we need these extra values, like not-T vs. F, and thus we have extra complications.]
Or take the liar sentence, ‘This sentence is false’. This was supposed to be an example of a sentence that is both true and false. Let’s tweak it a bit. Consider, instead, the sentence ‘This sentence is not true’. What is the truth value of this? If it is true, then what it says is the case; so it is not true. But if it’s not true, then, since that is what it says, it is true. Either way, it would seem to be both true and not true. Again, we have a contradiction on our hands. It’s not just that a sentence may take the values T and F; rather, a sentence can both be T and not be T.
(37)
Priest concludes: “It is situations of this kind that have made the subject of self-reference a contentious one, ever since Eubulides. It is, indeed, a very tangled issue” (37).
[The following is quotation.]
Main Idea of the Chapter
● Sentences may be true, false, both, or neither.
(quoted from Priest, 37, boldface his)
From:
Priest, Graham. Logic: A Very Short Introduction. Oxford: Oxford University, 2000.
Also mentioned:
Priest, Graham. In Contradiction: A Study of the Transconsistent. Oxford/New York: Clarendon/Oxford University, 2006 [first published 1987]