[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
§ 567
The incommensurability found in Spinoza's circle example "embraces in general the functions of curved lines and more precisely, leads to the infinite which mathematics has introduced with such functions, in general, with the functions of variable magnitudes" (see Spinoza Letter XII, Hegel's Commentary § 566). [Hegel here might mean that he deals with the space between curved lines of the circles much in the way that integral calculus does.] The infinite that Spinoza here articulates is what he considers the genuine mathematical qualitative infinite.
§ 568
The magnitudes of inequalities of space between the circles are variable, but not in the sense that the two numbers 2 and 7 are variable in the fraction 2/7; because even though we may substitute 4/14, 6/21 and so on to infinity, each time the figure represents the same value. Moreover, although the a and b in a/b may be replaced by any of an infinity of numbers, it still represents a determinate value, and also none of these substitutions changes the relation that this ratio expresses (see sections §§553 - 561). Thus the term "variable magnitude" is poorly chosen because it can be mistaken for these simpler forms of numerical variation.
§ 569
Hegel is interested in the "moments of a function with which higher analysis is concerned," and he first runs through the previous steps.
In the 2/7 and a/b, the 2 and the 7 each are "independent determinate quanta" whose relationship to each other is not essential to each individually as quanta. Likewise, the a and the b represent quanta that also remain what they are outside their relation to each other. Also, but ratios are fixed quantities, because their value is fully expressed in the related parts: the denominator is its unit, and the numerator is the amount of these units. So even if we substitute 4 and 14 for the 2 and 7, we still have the same quantum.
This is not so, however, in the function y2/x = p
To visualize it, we will solve it for y, and we get y = the square root of x. We might also consider another relation of powers, y = x squared. These two graphed would look like:
The perfectly diagonal line would represent x and y at the same order or power, x = y. For every change in x, there is a proportional change in y. So if x is 2, then y is 2 as well. This produces a straight line. Likewise, if there were co-efficients, like x = 2y, we still would obtain a straight line. This is equivalent to Oresme's uniformly difform motion.
(Thanks Jeff Babb)
But when there is a difference of power, then the relation is an exponential one, so that the graphed line becomes a curve whose rate of change itself changes. The further down the line on y = x-squared, the steeper it raises. And the further down the y = square root of x, the less steeply it raises.
Hegel considers this a variable magnitude, because the variation itself varies. He writes that even though x and y stand for determinate quanta, when they are put in an off-set power relation, their quotient varies in a way that is only partly related to the variance of each term, because when we vary x or y, the variance of their off-set power relation is not proportional to it, as is the case when they are of the same power.
this is solely because x has a relation, not to y, but to the square of y. The relation of a magnitude to a power is not a quantum, but essentially a qualitative relation; the power-relation is the feature which is to be regarded as the fundamental determination. But in the function of the straight line y = ax, a is an ordinary fraction and quotient; consequently this function is only formally a function of variable magnitudes, or x and y here are what a and b are in a/b that is, they are not in that determination in which the differential and integral calculus considers them.
[As we will see, calculus treats of these curves, which are thus differences of power relations.]
Calculus was originally hindered by efforts to include functions of the first degree and of the straight line, which stemmed from the "intrinsically correct demand for the generalisation of a method" that may base the calculus on specific determinateness, as if calculus were only concerned with variable magnitudes. But the magnitudes that vary are not calculus' concern, because it looks to the relations of powers which produce different results at different limits.
A great deal of formalism would, indeed, have been avoided if it had been perceived that the calculus is concerned not with variable magnitudes as such but with relations of powers.
§ 570
In differential calculus, the mathematical infinite becomes prominent again. In the above example where x and y are determined by power relations, the value for x and y still is supposed to signify a quanta. However, in calculus dx and dy are infinitesimal values and thus no longer signify quanta:
it is solely in their relation to each other that they have any meaning, a meaning merely as moments. They are no longer something (something taken as a quantum), not finite differences; but neither are they nothing; not empty nullities. Apart from their relation they are pure nullities, but they are intended to be taken only as moments of the relation, as determinations of the differential coefficient dx/dy.
[Compare with Deleuze from: Cours Vincennes - 22/04/1980
Differential calculus allows you to proceed directly to compare quantities raised to different powers. Moreover, it is used only for that.
Differential calculus finds its level of application when you are faced with incomparables, that is, faced with quantities raised to different powers. Why? In ax2+y, let us assume that by various means, you extract dx and dy. What is that? We will define it verbally, conventionally, we will say that dx or dy is the infinitely small quantity assumed to be added or subtracted from x or from y. Now there is an invention! ... The miracle dy/dx is not equal to zero, and furthermore: dy/dx has a perfectly expressible finite quantity. These are relative , uniquely relative. dx is nothing in relation to y, dy is nothing in relation to y, but then dy/dx is something. A stupefying, admirable, and great mathematical discovery. It's something because in an example such as ax2-by+c, you have two powers in which you have incomparable quantities: y2 and x. If you consider the differential relation, it is not zero, it is determined, it is determinable. The relation dy/dx gives you the means to compare two incomparable quantities that were raised to different powers since it operates a depotentialization of quantities. So it gives you a direct means to confront incomparable quantities raised to different powers. From that moment on, all mathematics, all algebra, all physics will be inscribed in the symbolism of differential calculus... It's the relation between dx and dy that made possible this kind of co-penetration of physical reality and mathematical calculus. (Deleuze, Cours Vincennes - 22/04/1980, French text here).]
We see that x and y may stand for definite quanta. But x is not in a relation with y. Rather, x is in a relation with y-squared, and only these two have a determinate quotient (p).
§ 571
In the calculus understanding of the infinite, the quantum is a genuine qualitative reality, "not merely as this or that quantum but as quantum generally." And yet, despite on the one hand it being considered not finite, this concept of infinity is still considered in calculus as a determinate quantum.
§ 572
Attacks on the mathematical infinite are leveled at this paradoxical notion of infinity in differential and integral calculus. Critics fail to recognize that this sort of infinity is a Notion more than a sensible reality. And when the calculus makes use of this notion of infinity, their methods are in complete contradiction with the usual finite mathematics.
§ 573
Mathematics considers these infinitesimal quantitative determinations as "vanishing magnitudes, i.e. magnitudes which are no longer any particular quantum and yet are not nothing but are still a determinateness relatively to an other." Thus mathematics takes infinitesimals as being in an intermediate state between being and nothingness, while yet also holding that such a state does not exist. Hegel already explained in Remark 4 that everything is ever becoming and thus always dually being and nothing. Moreover, this unity of being and nothing is not a "state," because a state is a determination that suggest stasis or worse a "diseased condition." On the contrary, the infinitesimal is a mean and unity whose truth is the "vanishing" and "the becoming."
§ 574
Another critique of the infinite is that it cannot be compared to another in terms of being greater or smaller, and thus "there cannot be a relation between infinites according to orders or dignities of the infinite, although in the science of infinitesimals these distinctions do occur." The presupposition that underlies this critique is that "greater" or "lesser" are determinations given to finite quanta compared to other quanta, and that "determinations which are no longer quanta no longer have any relationship to each other."
However, Hegel explains, when we put quanta into a relation, it is a ratio that is no longer a quantum (for rather it is qualitative, see § 552-§ 555). Quanta can be taken by themselves; and individually their value does not concern other quanta necessarily: "the nature of quantum is such that it is supposed to have a completely indifferent existence apart from its ratio, and its difference from another quantum is supposed not to concern its own determination."
However, "the qualitative is what it is only in its distinction from an other." The infinitesimal magnitudes of the calculus are more than just comparable values, rather, they exist only "as moments of comparison, i.e. of the ratio."
§ 575
Hegel will now discuss some of the definitions mathematics has so far given for the infinite, which will show that they are in accord with his Notion of the infinite.
§ 576
One might object that vanishing magnitudes cannot have a ratio on account of them vanishing before their ratios may be determined. However,
by the ratio of vanishing magnitudes is to be understood not the ratio before which and after which they vanish, but with which they vanish. (quacum evanescunt). Similarly, the first ratio of nascent magnitudes is that with which they become.
§ 577
Even though the demands of science did not require
By magnitudes is understood magnitudes in their vanishing, i.e. which are no longer quanta; also, not ratios of determinate parts, but the limits of the ratio. The meaning is, therefore, that with the vanishing of the quanta individually, the sides of the ratio, there also vanishes the ratio itself in so far as it is a quantum; the limit of the quantitative ratio is that in which it both is and is not, or, more precisely, in which the quantum has vanished, with the result that the ratio and its sides are preserved, the former only as a qualitative relation of quantity and the latter similarly as qualitative moments of quantity.
But Newton clarifies that even though there are final ratios for the vanishing magnitudes, there are yet no final magnitudes as indivibles, because to presume so would mean reducing a qualitative ratio to a quantitative unitary value "devoid of any relation at all."
§ 578
To avoid this mistake,
final ratios are not ratios of final magnitudes, but are limits to which the ratios of the magnitudes decreasing without limit are nearer than any given, i.e. finite, difference; the ratios, however, do not exceed these limits, for if they did they would become nullities.
Thus the final magnitudes could have been taken as invisibles, but his definition of the final ratio excludes that possibility. But, Hegel says,
§ 579
Elsewhere, namely in Carnot, there are similar descriptions based on the law of continuity that express the vanishing magnitudes that nonetheless retain their ratio.
§ 580
The true nature of the infinitesimal is not expressed as a continuity of a quantum diminishing to a value that is beyond the finite; rather it is the ratio that is continuous, and it continues until its constituent quanta (as finite and non-relational in themselves) come to vanish. Hegel says that this "purification of the quantitative ratio" is analogous to
empirical reality in terms of its Notion. The empirical reality is thereby raised above itself in such a way that its Notion contains the same characteristic features as it has itself, but these are grasped in their essentiality and are taken into the unity of the Notion in which they have lost their indifferent, Notion — less existence.
§ 581
§ 582
A problem with conceiving the infinitesimal as obtained by means of increment or decrement is that is that they are supposed to be neglected "not only in comparison with finite magnitudes, but also their higher orders in comparison with their lower, and even the products of several in comparison with a single one." This demand to neglect the magnitudes is more prominent in Leibniz, and it has given calculus the appearance of inexactitude. Wolf makes this neglect more intelligible by "polluting the pure Notion and setting in its place incorrect sensuous conceptions." For example, Wolf
compares the neglect of infinitesimals of higher orders relatively to lower with the procedure of a surveyor who, in measuring the height of a mountain is no less accurate if meanwhile the wind has blown away a grain of sand from the top; or with the neglect of the height of houses or towers when calculating lunar eclipses.
[The problem with this conception is it treats the infinitesimal in terms of an inexactitude.]
§ 583
Even though common sense might allow for the inexactitude Wolf describes, geometricians reject the notion. Mathematics itself is not like its practical application. Moreover, there are different ways to determine the differential, but all produce exactly the same result; hence it is not a product of inexactitude. And yet, differentiation still omits negligible values.
§ 584
Euler, taking a Newtonian approach, argues that differential calculus deals with the ratios of increments of a magnitude, “but that the infinite difference as such is to be considered as wholly nil:”
the infinite difference is a nil only of quantum, not a qualitative nil, but as a nil of quantum it is a pure moment of the ratio only. It is not a quantitative difference; but for that reason it is, on the one hand, altogether wrong to speak of those moments which are called infinitesimals, also as increments or decrements and as differences.
For Euler, something is added-to or subtracted-from the original finite magnitude, and this is an arithmetical external operation. But the transition of the variable magnitude’s function to the differential is a “reduction of the finite function to the qualitative relation of its quantitative determinations.” However, he falls into error by saying that the increments themselves are zeros, because “a zero no longer has any determinateness at all.” Euler, then, does not realize the “qualitative determinations of quantity which, if they were torn out of the ratio and regarded as quanta, would be only zeros.”
§ 585
Lagrange thought that we may conceive the ratio of two magnitudes so long as they remain finite; however, "this ratio does not present any clear and definite concept to the intellect as soon as its terms become simultaneously zero." Instead, we must transcend the mere negativity of their zero quantitative value, and grasp them positively as qualitative moments.
§ 586
Hegel is satisfied that these examples are adequate to "show clearly enough that the genuine Notion of the infinite is, in fact, implied in them, but that the specific nature of that Notion has not been brought to notice and grasped." As a result, when the method of infinitesimals is applied, the genuine Notion of the infinite bears no influence. On the contrary, quantity's finite determinateness returns, and these methods must still make use of the conception of a quantum which is merely relatively small. Calculus requires that we subject the infinitesimals to ordinary arithmetical operations of addition and so forth. These operations are based on the nature of finite magnitudes. Calculus must justify its method, which on the one hand treats these finite magnitudes as increments or differences, while on the other hand disregards their quantitative value "after it had just applied forms and laws of finite magnitudes to them."
§ 587
The modern mathematicians wanted both to give evidence for differential calculus by means of a strictly geometrical method and as well to offer proofs as rigorous as those of the ancient mathematicians. But it is not proper to the higher nature of calculus to seek geometrical evidence like finite mathematics does. Thus Hegel will only deal with mathematics’ efforts to attain “the rigour of proof of the ancients” (Hegel here quoting Lagrange).
§ 588
Some mathematicians attempted to dispense altogether with the concept of the infinite. Landen, for example, devised a purely analytical method – much like Descartes' tangential method – that does not employ infinitesimal differences, but begins instead with different values for variable magnitudes, and then it equates them. But this method is not technically calculus.
§ 589
Such earlier moderns as Fermat and Barrow initially applied infinitesimals in a way that later became the differential and integral calculus. Leibniz and such followers as Euler omitted infinitesimal differences and their higher powers, “solely on the ground that they vanish relatively to the lower order.”
This is for them the sole basis of the fundamental principle, namely the determination of that which is the differential of a product or a power, for the entire theoretical teaching reduces to this.
For them, the
cardinal principle adopted in relation to curves is that the elements of the curves, namely the increments of abscissa and ordinate, have the relation to each other of subtangent and ordinate.
So in order to obtain similar triangles,
the arc which forms the third side of a triangle to the two increments of the characteristic triangle (as it rightly used to be called), is regarded as a straight line, as part of the tangent and one of the increments therefore as reaching to the tangent.
But by making these assumptions, the determinations are on the one hand raised above the nature of finite magnitudes; and yet on the other hand, the method – which is only valid for finite magnitudes and which forbids omitting values no matter how insignificant – nonetheless is applied to the infinitesimal.
§ 590
remove the arithmetically incorrect omission of the products of infinitesimal differences or higher orders of them in the finding of differentials. He finds the differentials of products — from which the differentials of quotients, powers, etc., can then be easily derived — in the following way. The product of x and y, when each is taken as reduced by half of its infinitesimal difference, becomes xy - xdy/2 - ydx/2 + dxdy/4;
[because when multiplied in the order of first-outer-inner-last: (x – dx/2) (y – dy/2) = xy – xdy/2 – ydx/2 + dxdy/4]
but if x and y are made to increase by the same amount, it becomes xy + xdy/2 + ydx/2 + dxdy/4.
[That is, (x + dx/2) (y + dy/2) = xy + xdy/2 + ydx/2 + dxdy/4].
Now when the first product is subtracted from the second, ydx + xdy remains as a surplus and this is said to be the surplus of the increase by a whole dx and dy, for this increase is the difference between the two products; it is therefore the differential of xy.
[(xy + xdy/2 + ydx/2 + dxdy/4) - (xy – xdy/2 – ydx/2 + dxdy/4) =
(xy + xdy/2 + ydx/2 + dxdy/4 + -xy + xdy/2 + ydx/2 - dxdy/4) =
(2xdy/2 + 2ydx/2) cancel the 2’s
(xdy + ydx)]
We applied half a decrease and half an increase to both products, so we would expect the difference between the two values to come out even. But instead there is a surplus value xdy +ydx which must be the differential value of the product of xy].
Hegel finds
it is not true that (x + dx/2) (y + dy/2) - (x - dx/2) (y - dy/2) = (x + dx) (y + dy) - xy.
§ 591
§ 592
Lagrange demonstrated that
For example, it is well known that in mechanics the terms of the series in which the function of a motion is developed are given a specific meaning, so that the first term or the first function refers to the moment of velocity, the second to the accelerating force and the third to the resistance of forces. Here, then, the terms of the series are not to be regarded merely as parts of a sum, but rather as qualitative moments of a whole determined by the concept. In this way, the omission of the rest of the terms belonging to the spuriously infinite series acquires an altogether different meaning from omission on the ground of their relative smallness.
[Hegel proceeds to give a detailed explanation of Langrange's superior treatment of the problem].
Thus
§ 593
The problem of the above example can be solved if we based our operation on the qualitative meaning rather than on the formalism which links the differential only to the difference between a function and its varied magnitude. Thus the differential of xn
is completely exhausted by the series’ first term.
Thus the omission of the rest of the terms is not on account of their relative smallness; and so there is no assumption of an inexactitude, an error or mistake which could be compensated or rectified by another error — a point of view from which Carnot in particular justifies the ordinary method of the infinitesimal calculus.
The differential is completely given by the first term, because we are dealing not with a sum but a with a relation. And, we do not determine differentials of higher orders by summing a series’ continuation, but by means of a
repetition of one and the same relation which alone is desired and which is thus already completely given in the first term. [Compare to Wronski vs. Lagrange and Carnot]
§ 594
Carnot clearly elucidates the above ideas in his explanation of the infinitesimal methods. However, when he describes their practical application, he espouses strange ideas about the relative infinite smallness of omitted terms. Rather than justifying the nature of the method, he instead defends it on the grounds of its accuracy.
§ 595
Lagrange avoided the problems with the notion of the infinitely small by reverting to
His method
rests on the fundamental principle that the difference, without becoming zero, can be assumed so small that each term of the series is greater than the sum of all the following terms.
Lagrange’s procedure begins by increasing the function’s difference to create a variable magnitude, which introduces “the troublesome series of the original function.”
The subsequent terms in the series are thought to constitute a sum whose relative smallness justifies their omission.
Thus again, on the one hand, terms are omitted because of qualitative irrelevance and not quantitative insignificance, while on the other hand, this omission plays no vital role in the notion of the differential coefficient.
§ 596
Lagrange argues that the limit method does not apply well and that the expression limit does not present any definite idea.
Hegel holds, however, that
the idea of limit does indeed imply the true category of the qualitatively determined relation of variable magnitudes above-mentioned; for the forms of it which occur, dx and dy, are supposed to be taken simply and solely as moments of dy/dx, and dy/dx itself must be regarded as a single indivisible symbol.
§ 597
By means of derivation, a limit determines a certain value for a function. From this definition alone, we only know that
the infinitely small which presents itself in the differential calculus as dx and dy, does not have merely the negative, empty meaning of a non-finite, non-given magnitude, as when one speaks of 'an infinite multitude', 'to infinity', and the like, but on the contrary has the specific meaning of the qualitative nature of what is quantitative, of a moment of a ratio as such.
But this definition alone does not tell us the nature of the relation between a limit and a function.
But the limit limits something in that it “expresses a certain value which lies in the function of a variable magnitude.”
It is supposed to be the limit of the ratio between the two increments by which the two variable magnitudes connected in an equation (one of which is regarded as a function of the other), are supposed to have been increased; the increase is taken here as quite undetermined and so far no use is made of the infinitely small.
And yet, the method of finding the limit involves the same inconsistencies we found in the other procedures.
This way is as follows: if x = fx, then when y becomes y + k, fx is to change into fx + ph + qh2 + rh3
and so on; thus k = ph + qh2, etc., and k/h = p + qh + rh2, etc.
Now if k and h vanish, the right-hand side of the equation also vanishes with the exception of p; now p is supposed to be the limit of the ratio of the two increments. It is clear that while h, as a quantum, is equated with 0, k/h nevertheless is not at the same time equal to 0/0 but is supposed still to remain a ratio.
§ 598
The concept of limit supposedly avoids this above inconsistency that h has quantitative value of zero, but when put in ratio with the other infinitesimal value it is not 0/0 but still a ratio.
p is, at the same time, supposed to be not the actual ratio, which would be 0/0 but only that specific value to which the ratio can infinitely approximate, i.e. can approach so near that the difference can be smaller than any given difference.
Our knowing that the quantitative difference of the infinitesimal value is qualitative and not quantitative has not saved us from concluding that dy/dx = 0. But if instead dy/dx = p, and thus we assume it to be a definite quantitative ratio, the we likewise encounter difficulty in equating k with such that k/h = p. And yet if we hold that k/h = 0, then what quantitative value would we assign p? Hegel replies: “it is a coefficient derived in such and such a way — the first function, derived in a certain specific manner, of an original function.” Lagrange’s method, in fact, assumed this meaning. If we take up this sense as well, then differential calculus thereby making use of the concept of limits would have no need for infinitely or arbitrarily small increments. As well, we would not have the problem of accounting for all the additional terms of the series added to the first coefficient, because they resulted from the increments. And finally, this meaning for p would eliminate such related notions as the infinite, infinite approximation, continuous magnitude, nisus, becoming, and occasion of a variation.
§ 599
In brackets, Hegel notes that continuous or fluent magnitudes are considered in terms of the external and empirical variation of magnitudes, but no satisfactory definition has been given based on the law of continuity.
§ 600
Now Hegel must expand the meaning and value of p beyond its merely being considered “a function derived from the expansion of a binomial.” But first Hegel will explain why the notion of approximation has made it more difficult to understand the calculus in terms of qualitative determinateness.
§ 601
We saw previously how
infinitesimals express the vanishing of the sides of the ratio as quanta, and that what remains is their quantitative relation solely as qualitatively determined; far from this resulting in the loss of the qualitative relation, the fact is that it is just this relation which results from the conversion of finite into infinite magnitudes.
So in the final ratio, the quanta of abscissa and ordinate vanish, for example; yet the ratio’s sides remain: one is still an element of the ordinate, the other of the abscissa.
[When we consider Leibniz’ triangle example], it might seem as though in the infinite approximation “the previously distinguished ordinate is made to pass over into the other ordinate, and the previously distinguished abscissa into the other abscissa." But this is not what happens.
the element of the ordinate is not to be taken as the difference of one ordinate from another ordinate, but rather as the difference or qualitative determination of magnitude relatively to the element of the abscissa; the principle of the one variable magnitude relatively to that of the other is in reciprocal relation with it. The difference, as no longer a difference of finite magnitudes, has ceased to be manifold within itself; it has collapsed into a simple intensity, into the determinateness of one qualitative moment of a ratio relatively to the other.
[Thus the dy added to the y of the ordinate is not the addition of an ordinate value, because it is a qualitative relationship between the ordinate as a variable magnitude to the abscissa as a variable magnitude. Because the difference between dy and y is no longer a difference of finite magnitudes, it is a pure intensive magnitude that is a qualitative moment of a ratio in relation to the other part of the ratio.]
§ 602
What Hegel has established above has been obscured by the incorrect concept of dy as a difference or increment between two values of y, of the ordinate for example. In this mistaken conception, the limit is not taken to be a ratio, but
counts only as the final value to which another magnitude of a similar kind continually approximates in such a manner that it can differ from it by as little as we please, and that the final ratio is a ratio of equality.
When incorrectly conceiving the infinitesimal difference as a fluctuation of a difference of one quantum from another quantum, we neglect the fact that the qualitative nature of dx lies in its ratio relation to dy and not x.
§ 603
The incorrect view considers increments or infinitesimals only in terms of the quantum that vanishes in them and as a limit; thus, they are thought to be unrelated moments. If we followed this line of thinking, we would wrongly conclude that we may equate in the final ratio the related quanta, for example we might incorrectly equate the “abscissa and ordinate, or even sine, cosine, tangent, versed sine, and what not.” Hence arcs have been considered as tangents, despite their incommensurability; for they are both of different qualities. We might also make the mistake of thinking that a curved line is made up of infinitely many infinitely small constituent lines, and thus we might incorrectly consider a curve and a straight line as of the same sort.
Now however Hegel describes how in differentiation the straight line passes into the curved line. By definition, “a straight line is the shortest distance between two points,” so “its difference from the curved line is based on the determination of amount, on the smaller amount of what is differentiated in this manner, a determination, therefore, of a quantum.”
But this determination vanishes in the line when it is taken as an intensive magnitude, as an infinite moment, as an element, and with it, too, its difference from the curved line which rested merely on the difference of quantum. As infinite, therefore, the straight line and arc no longer retain any quantitative relation nor consequently, on the basis of the assumed definition, any qualitative difference from each other either; on the contrary, the former passes into the latter.
[In other words, along a curve there are differential moments when the curve is both changing direction curvilinearly while tending linearly, to use the wrong metaphors; more accurately, when it is both a curve and straight line.]
§ 604
Another similar mistake is to consider infinitely small parts of a common whole as all equal to each other. When we apply this erroneous notion to an object “heterogeneous within itself, i.e. an object whose quantitative determination is essentially non-uniform,” what results is an “inversion” which is also found in a proposition of mechanics stating that “infinitely small parts of a curve are traversed in equal, infinitely small times in a uniform motion,” which is said of a non-uniform movement in which finite unequal parts of the curve are traversed equal finite parts of time.
One reason that calculus has been construed in physical and geometrical terms is that it was often used to solve physics problems and demonstrated using geometrical representations.
§ 605
Modern mechanics employs calculus notions without first determining whether there is anything physical that corresponds to the pure mathematical abstractions.
It is announced as a triumph of science that by means of the calculus alone, laws are found transcending experience, that is, propositions about existence which have no existence.
But in the earlier “naïve” period of calculus, mathematicians aimed to assigned real corresponding meanings to their geometrical diagrams.
§ 606
The “nebulous conception of the infinitely small” has been accepted on the basis of what seemed to be adequate mathematical proof. Empirically discovered laws seem to be determinable by mathematics alone, but for Hegel these proofs are arranged so that the empirical result will correspond. Hegel includes
§ 607
mathematics is altogether incapable of proving quantitative determinations of the physical world in so far as they are laws based on the qualitative nature of the moments [of the subject matter]
Thus unlike philosophy, science does not start from the Notion, and hence the “qualitative element” lies outside its scope. Efforts to “uphold the honour of mathematics” by rigorously proving all propositions have caused us to forget mathematics' limitations. Thus although mathematics cannot prove empirical findings, it has wrongly been used for that purpose, as for example with
Remark 2: The Purpose of the Differential Calculus Deduced from its Application
§ 608
Hegel will not consider the concrete application of calculus notion.
The whole method of the differential calculus is complete in the proposition that dxn = nx(n - 1)dx,
or (f(x + i) - fx)/i = P,
that is, is equal to the coefficient of the first term of the binomial x + d, or x + 1, developed according to the powers of dx or i.
Hegel says we need not learn anything beyond these propositions, because the rest follows “mechanically.” What is left to explain is “the omission of all the terms except the first, of the series arising from the expansion.”
§ 609
the arbitrary omission of terms arising from the expansion of a function is absolutely contrary to all mathematical principles.
It is a practice that results from “tangential methods” indirectly related to the calculus.
it was only later that mathematicians reflected on the nature of the method after it had been extended to other objects, and reduced it to abstract formulae which they then also attempted to raise to the status of principle.
§ 610
Hegel ask now about the nature of the transition from the theoretical development of the calculus to its application.
§ 611
The specifically qualitative character of quantity is first indicated in the quantitative relation as such; but it was already asserted in anticipation when demonstrating the so-called kinds of reckoning (see the relative Remark), that it is the relation of powers (still to be dealt with in its proper place) in which number, through the equating of the moments of its Notion, unit and amount, is posited as returned into itself, thereby receiving into itself the moment of infinity, of being-for-self, i.e. of being self-determined. Thus, as we have already said, the express qualitative nature of quantity is essentially connected with the forms of powers, and since the specific interest of the differential calculus is to operate with qualitative forms of magnitude, its own peculiar subject matter must be the treatment of forms of powers, and the whole range of problems, and their solutions, show that the interest lies solely in the treatment of determinations of powers as such.
§ 612
By taking the relations of powers (and the qualitative nature of quantity), we may dispense with the more problematic notions of “variable, continuous or infinite magnitudes or even of functions generally.” But our foundation is still too general because there are other operations dealing with power determinations, for example, “the raising to a power, extraction of a root, treatment of exponential magnitudes and logarithms, series, and equations of higher orders.” But as we see from its applications, the peculiar interest of calculus are the various relations in which determinations of powers can be put. Making these power determinations constitutes the actual procedure of calculus, which itself preceded the theories given to justify the methods.
§ 613
The subject of our investigation are the “equations in which any number of magnitudes (here we can simply confine ourselves to two) are combined into a qualitative whole.” Firstly, these equations have their determinateness a) in empirical magnitudes which are their fixed limits and b) “in the kind of connection they have with these limits and with each other as is generally the case in an equation.” Secondly, “one aspect of the determinateness of these magnitudes is that they are — or at least one of them is present in the equation in a higher power than the first.”
§ 614
Two notes,
1) magnitudes are variables with undetermined values,
but if one of them does receive a completely determined value, i.e. a numerical value, from outside, then the other too, is determined, so that one is a function of the other.
2) The “so-called constant” is
an indifferent empirical magnitude determining the variables only with respect to their empirical quantum as a limit of their minimum and maximum.
Hence the constants are important determinations of the function. But they may also themselves serve as functions. Hegel writes:
in the expansion of the binomial generally, the constant which is the coefficient of the first term of the development is the sum of the roots, the coefficient of the second is the sum of the products, in pairs, and so on; here, therefore, the constants are simply functions of the roots.
[I offer as a possible explanation these the binomial expansion which resembles Pascal's triangle:
Here we see that each coefficient is the sum of the two directly above it, and the first numbers of the sequence match the powers of the binomial, so in a sense perhaps these constants might be considered as functions. But a better explanation should replace mine. ]
Where, in the integral calculus, the constant is determined from the given formula, it is to that extent treated as a function of this,
which we see in the power law.
§ 615
Now the difference between variables as considered in the differential calculus, and in their character as factors in indeterminate problems, must be seen to consist in what has been said, namely, that at least one of those variables (or even all of them), is found in a power higher than the first; and here again it is a matter of indifference whether they are all of the same higher power or are of unequal powers; their specific indeterminateness which they have here consists solely in this, that in such a relation of powers they are functions of one another.
That is to say, on account of the power rule, the function which is the differential is of a lower power than the function being differentiated, and hence the relation between a function and its derivate is primarily a relation of powers.
The alteration of variables obtains its meaning
in the power-relation, which does not have a quantum for its exponent and which forms the non-quantitative, permanent determinateness of the ratio of the variables.
Hegel then explains that the first exponential power is only a power in relation to the higher powers, because when we differentiate a point on a straight line, the tangent is that very same line.
§ 616
(b) Our treatment of basic equations reveals,
power is taken as being within itself a relation or a system of relations. We said above that power is number which has reached the stage where it determines its own alteration, where its moments of unit and amount are identical — as previously shown, completely identical first in the square, formally (which makes no difference here) in higher powers.
[Let's consider first the function y = 2 which means that there is no relation of variance with x, so this is like Oresme's uniform motion:

(Thanks Jeff Babb)
Now we will consider the value for y = 2x :
Here we see that there is a relation of variance between x and y. As x increases, y increases doubly, but uniformly so; y is always twice x, so they are on the same level or power. This is like Oresme's uniformly difform motion.
(Thanks Jeff Babb)
Hegel says that there is no reason to differentiate a point on such a line, because it would be the same ratio as the line itself. Now we will consider the graph for x squared:
Here we see that the y value is not twice the x. This is because the y and the x do not relate to each other, rather the y relates only to the x squared. This is like Oresme's difformly difform motion.
(Thanks Jeff Babb)
Differentiating a point on such a line would produce a new tangent line, hence there is reason to apply calculus once there is a difference of powers between the variables. Hegel says that "moments of unit and amount are identical." Hegel defines amount as the discrete quantitative value of the number, and the unit as the "continuity of the amount." We can see in the x-squared diagram how it is that the continuity of the value change is identical with its numerical value. We see that there is a continuous disproportioning of the relation between y and x, a continuous difforming that continuously doubles. It is in this way that the power's numerical value, the discrete number two, matches is continuity, its continually two-ing or doubling or squaring. Because the two-ness of the power determines the rate by which its change changes, that is, a continual doubling, Hegel says that the power determines its rate of alteration. Hegel also says that the power's amount and unit are completely identical in the square, and "formally" so in the higher powers. He also says that "the power is taken as being within itself a relation or a system of relations." To understand these points, we will examine the series for x raised to the second, third, and forth power. We see that when we take the squares for the first 9 numbers, we obtain the second row of values:
Now we will look at the differences in value between each squared value:
What we notice is that there is a difference of 2 between these differences of squares:
Thus the differences of the differences of squares equals the value of the exponent or power. Now we will consider x to the third power:
Here the differences of the differences did not produce a pattern, but the differences of the differences of the differences are equal to 6, which is 3 times the value of the previous power, 2.When we do the same for x to the fourth power, we obtain:
Here we needed to go to the differences of the differences of the differences of the differences in order to obtain the uniform difference 24, which is 4 times 3 times 2. So we see that with the power of two, the continuity of change was uniform: the differences in the increases were continually by units of two. But for the higher powers, the differences of the differences of the increases were not equal to the power, but equal to that power times the value of the lower power, so this is why they are only formally identical, perhaps. We also see that a power is a relation, because it is a relation of changing values, and the higher powers, as related to the lower ones, consistute a "system of relations."
Hegel goes on to say that
Now power is number (magnitude as the more general term may be preferred, but it is in itself always number), and hence a plurality, and also is represented as a sum; it can therefore be directly analysed into an arbitrary amount of numbers which have no further determination relatively to one another or to their sum, other than that together they are equal to the sum.
So for example, 3 squared equals 9, which we can give as 7 + 2. The seven and two have no special relation to each other, except when summed, then their total value equals 3 squared. He continues:
But the power can also be split into a sum of differences which are determined by the form of the power.
If we recall from the two squared:
we can take the first 5 differences and add them:
(1 - 0) + (4 - 1) + (9 - 4) + (16 - 9) + (25 - 16) = 25 or 5 squared.
He goes on to write:
If the power is taken as a sum, then its radical number, the root, is also taken as a sum.
So when we sum the differences of the constituents of a power, and when we sum up the quantity of those differences, we obtain the same number as the root; so for example, when we summed the first set of differences that come to equal 5 squared, we found that we needed to find the first 5 differences; so, the radical is the sum of the number of differences in series whose total value equals the powered value.
And then he writes:
The sum which the root is supposed to be, when reduced to its simple determinateness, i.e. to its genuine universality, is the binomial; all further increase in the number of terms is a mere repetition of the same determination and therefore meaningless.
[It springs solely from the formalism of that generality to which analysis perforce lays claim when, instead of taking (a + b)n
for the expansion of powers, it gives the expression the form of (a + b + c + d...)n
as happens too in many other cases; such a form is to be regarded as, so to speak, a mere affectation of a show of generality; the matter itself is exhausted in the binomial. It is through the expansion of the binomial that the law is found, and it is the law which is the genuine universality, not the external, mere repetition of the law which is all that is effected by this a + b + c + d ...]
For example, we could write 3 squared as either (2 + 1)(2 +1) or as (1 + 1 + 1)(1 + 1 + 1). If we multiply them out as though they were variables, rather than summing first then multiplying, for the first we get 4 + 2 + 2 + 1, which equals 9, and in the second case we get 1 + 1 + 1+ 1+ 1+ 1+ 1+ 1+ 1, which also equals 9. Hegel's point seems to be that we need only represent powers when as sums in binomial form, because implied in it already are the more elaborate forms.
§ 617
The sole point of importance here is the qualitative determinateness of the terms resulting from the raising to a power of the root taken as a sum, and this determinateness lies solely in the alteration which the potentiation is. These terms, then, are wholly functions of potentiation and of the power.
The final values after the power-raising are the functions of the power's potentiation, and the sequence of sums depends on the the special theory of series.
§ 618
Above we regarded potentiation in terms of binomial expansion:
This exposition started from the sum as such for the expansion of the power, i.e. for obtaining the functions of its potentiation; but what is concerned here is not a sum as such, or the series arising from it; what is to be taken up from the sum is only the relation.
This is just the simple relation is merely the plussing or addition, which is the only relation needed to determine the "functions produced by the expansion of the power."
§ 619
But every power is already an equation, because it is always equal to some product or can be put in equation form ym = axn,
so it is “already a complex of several (variable) magnitudes which contains a power determination of them.” Each of the variables in the complex is “posited simply as in relation to the others with the meaning, one could say, of a plus implicit in it — as a function of the other variables.” [Because we may reduce to binomial, each term implies a plus relation to the other terms]. The functional character of these terms determines them as “a plus,” which, because the plus is implicit in a function, it is “wholly indeterminate,” “not an increase or an increment, or anything of that nature,” [because it is an implicit operation]. But even though we can consider a power in terms of its internal functional relations, “such functions containing a relation of powers,” considering powers in this way is just a possibility for construing them and is really a matter of choice whether we do so or not, depending on the utility of such a transformation.
620
Hegel summarizes that the above ways of representing functions of potentiation of a variable as containing a sum complex within itself, served on the one hand to indicate the nature of these functions, but on the other hand to show how they are found.
§ 621
However, this “increment” is not supposed to be quantum, because it is just a “form,” “the whole value of which is that it assists the development.”
Both Euler and Lagrange admit that “what is wanted is only the resulting power determinations of the variables, the so-called coefficients, namely, of the increment and its powers, according to which the series is ordered and to which the different coefficients belong.”
Recall Lagrange's use of the Taylor Series:
[Lagrange then identifies the functions p, q, r, ... with f 'x, (f ''x/2), (f '''x/3!), ... , where f 'x, f ''x, f '''x, and so on are the successive derivatives of the function fx. See the Taylor Series]
Hegel considers the i as the increment, because as “the one” it does not alter the value. However, the dx, “which is burdened with the false idea of a quantitative difference,” has an “appearance and pretension of a quantum and its powers” that must be avoided.
Hegel continues: "abstraction must be made from the series and from the determination of the coefficients according to their place in the series; the relation between all of them is the same; the second function is derived from the first in exactly the same manner as this is from the original function, and for the function counted as second, the first derived function is itself original."
[The whole series itself equals the original function, as we see above. And each is determined the same way: as a derivation of the previous one.]
But the essential point of interest is not the series but simply and solely the determination of the power resulting from the expansion in its relation to the variable which for the power determination is immediate.
[So regarding the contents of an expansion, of either the Taylor form, the previous polynomial form, or whatever form it is Hegel refers to here, we are not concerned so much with the contents of the series as much as the power its sum produces.]
§ 622
Hegel now asks what the applications are when finding "the function determined by the expansion of the power."
§ 623
This expansion of the powers that produces the functions of their potentiation, contains firstly and simple "the reduction of the magnitude to the next lower power."
Space's three dimensions of height, length and breadth, or geometrically, line, surface and total space can be taken "in their simplest forms and with reference to self-determination and consequently to analytical dimensions," which produces the straight line, plane surface and surface taken as a square, and the cube.
The straight line has an empirical quantum, but with the plane there enters the qualitative element, the determination of power. ... With this there arises, too, the need to pass from a higher power to a lower, and vice versa, when, for example, linear determinations are to be derived from given equations of the plane, or vice versa.
As well motion involves "the quantitative relation of the space traversed to the time elapsed," which manifests in different determinations of motion: simply uniform, or uniformly accelerated [Oresme's uniformly difform motion
] or alternately uniformly accelerated and uniformly retarded self-returning motion.
since these different kinds of motion are expressed in accordance with the quantitative relation of their moments, of space and time, their equations contain different determinations of powers, and when it is necessary to determine one kind of motion, or a spatial magnitude to which one kind of motion is linked, from another kind of motion, the operation also involves the passage from one power-function to another, either higher or lower.
§ 624
The operation of depotentiating an equation considered according to the derivative functions of its variables, yields a result which, in itself, is no longer truly an equation but a relation; this relation is the subject matter of the differential calculus proper. This also gives us, secondly, the relation of the higher power form (the original equation) itself to the lower (the derivative).
Let us start by considering the first relation; for the determination of its moment (to be taken from the application, in which lies the interest of the operation) we shall take the simplest example from curves determined by an equation of the second degree. As we know, the relation of the co-ordinates is given directly by the equation in a power form. From the fundamental determination follow the determinations of the other straight lines connected with the co-ordinates, tangent, subtangent, normal, and so on.
Hegel considers for his first example
curves determined by an equation of the second degree. As we know, the relation of the co-ordinates is given directly by the equation in a power form. From the fundamental determination follow the determinations of the other straight lines connected with the co-ordinates, tangent, subtangent, normal, and so on.
§ 626
But the tangent lines are of a power lower than the original function. Differential calculus makes the transition from the higher powered equation to the lower one by means of derivation.
§ 627
Newton's teacher, Isaac Barrow, was only able to describe this differential operation in an "empirical manner." His procedure, which is based on the method of indivisibles, rejects
as superfluous the terms which, as a result of the expansion of the equations, appear as powers of the said increments or as products (etenim isti termini nihilum valebunt); similarly, the terms which contain only magnitudes to be found in the original equation are to be rejected (the subsequent subtraction of the original equation from that formed with the increments).
We see something similar in the methods of Roberval and Fermat. Many during these times tried to find similar methods, which was "easy," because "the inventors had found only an empirical, external rule, not a method, i.e. nothing derived from established principles."
Leibniz and Newton "opened up new paths for the sciences" by gernalizing these procedures, but also felt the need "to wrest free the procedure from the shape of merely external rules and to try to procure for it the necessary justification."
§ 628
Hegel analyses the method further.
Firstly the power forms (of the variables of course) contained in the equation are reduced to their first functions. But the value of the terms of the equation is thereby altered; there is now no longer an equation, but instead only a relation between the first function of the one variable and the first function of the other.
That is to say, we obtain the ratio of dy/dx.
Instead of px = y2
we have p : 2y,
or instead of 2ax - x2 = y2,
we have a - x : y,
the relation which later came to be designated dy/dx, [because the x is removed, and the x and y are lowered a power, leaving 2a - 2x and 2y. Divide all by 2 to get final differential ratio.]
Although the equation represents a curve, the differential relation "which is completely dependent on it and derived from it (above, according to a mere rule), is, on the contrary, a linear relation with which certain lines are in proportion."
Hegel then explains that these derived lines are the tangents, which the ancient Greeks determined " an ingenious geometrical manner," and moderns have discovered it by means of an "empirical procedure."
On the one hand, the differential method was "methodically conceived and executed; but on the other hand the imaginary increments of the co-ordinates and an imaginary characteristic triangle formed by them and by an equally imaginary increment of the tangent, have been invented" so to find the tangent.
From the translation:
§ 567
The incommensurability which lies in Spinoza's example embraces in general the functions of curved lines and more precisely, leads to the infinite which mathematics has introduced with such functions, in general, with the functions of variable magnitudes. This infinite is the genuine mathematical qualitative infinite which Spinoza also had in mind. We shall now consider this determination here in detail.
§ 568
First of all, as regards the category of variability which is accorded such importance and which embraces the magnitudes related in these functions, it is to be noted that these magnitudes are not supposed to be variable in the way that the two numbers 2 and 7 are in the fraction 2/7: their place can equally well be taken by 4 and 14, 6 and 21, and by other numbersad infinitum without altering the value of the fraction; and still more in a/b, can a and b be replaced by any arbitrary number without altering what a/b is intended to express. Now in the sense that in the place, too, of x and y of a function, there can be put an infinite, i.e. inexhaustible, multitude of numbers, a and b are just as much variable magnitudes as the said x and y. The expression 'variable magnitudes' is therefore very vague and ill-chosen for those determinations of magnitude whose interest and manner of treatment lie in something quite distinct from their mere variability.
§ 569
In order to make clear wherein lies the true character of those moments of a function with which higher analysis is concerned, we must once more run through the stages to which we have already drawn attention. In 2/7 or a/b, 2 and 7 are each independent determinate quanta and the relation is not essential to them; a and b likewise are intended to represent quanta which remain what they are even outside the relation. And further, 2/7 and a/b are each a fixed quantum, a quotient; the ratio constitutes an amount, the unit of which is expressed by the denominator and the amount of these units by the numerator, or conversely; even if 4 and 14, and so on, are substituted for 2 and 7, the ratio, also as a quantum, remains the same. But now in the function y2/x = p, for example, this is essentially changed; here, it is true that x and y can stand for definite quanta, but only x and y2 have a determinate quotient, not x and y. Hence not only are these sides of the ratio xand y, not any determinate quanta, but, secondly, their ratio is not a fixed quantum (nor is such a quantum meant as in the case of a and b), not a fixed quotient, but this quotient is, as a quantum, absolutely variable. But this is solely because x has a relation, not to y, but to the square of y. The relation of a magnitude to a power is not a quantum, but essentially aqualitative relation; the power-relation is the feature which is to be regarded as the fundamental determination. But in the function of the straight line y = ax, a is an ordinary fraction and quotient; consequently this function is only formally a function of variable magnitudes, or x and y here are what a and b are in a/b that is, they are not in that determination in which the differential and integral calculus considers them. On account of the special nature of the variable magnitudes in this mode of consideration, it would have been fitting to have introduced both a special name for them and other symbolsthan those generally used for unknown quantities in any finite equation, determinate or indeterminate; for there is an essential difference between those magnitudes and such quanta which are merely unknown, but are in themselves completely determined or are a definite range of determinate quanta. It is, too, only because of a lack of awareness of what constitutes the peculiar interest of higher analysis and of what has led to the need for and invention of the differential calculus, that functions of the first degree and the equation of the straight line are themselves included in the treatment of this calculus; such formalism originates partly, too, in the mistake of imagining that the intrinsically correct demand for thegeneralisation of a method has been fulfilled when the specific determinateness on which the need for the calculus is based is omitted, as if in this domain we were concerned only with variable magnitudes. A great deal of formalism would, indeed, have been avoided if it had been perceived that the calculus is concerned not with variable magnitudes as such but with relations of powers.
§ 570
But there is still another stage where the peculiar character of the mathematical infinite becomes prominent. In an equation in which x and y are determined primarily by a power-relation, x and y as such are still supposed to signify quanta; now this significance is altogether and completely lost in the so-called infinitesimal differences. Dx, dy, are no longer quanta, nor are they supposed to signify quanta; it is solely in their relation to each other that they have any meaning, a meaning merely as moments. They are no longer something (something taken as a quantum), not finite differences; but neither are they nothing; not empty nullities. Apart from their relation they are pure nullities, but they are intended to be taken only as moments of the relation, as determinations of the differential coefficient dx/dy.
§ 571
In this concept of the infinite, the quantum is genuinely completed into a qualitative reality; it is posited as actually infinite; it is sublated not merely as this or that quantum but as quantum generally. But the quantitative determinateness remains as element of the principle of the quanta, or, as has also been said, the quanta remain in their first concept.
§ 572
It is this concept which has been the target for all the attacks made on the fundamental determination of the mathematics of this infinite, i.e. of the differential and integral calculus. Failure to recognise it was the result of incorrect ideas on the part of mathematicians themselves; but it is the inability to justify the object as Notion which is mainly responsible for these attacks. But mathematics, as we remarked above, cannot evade the Notion here; for, as mathematics of the infinite, it does not confine itself to the finite determinateness of its objects (as in ordinary mathematics, which considers and relates space and number and their determinations only according to their finitude); on the contrary, when it treats a determination taken from ordinary mathematics, it converts it into an identity with its opposite, e.g. converting a curved line into a straight one, the circle into a polygon, etc. Consequently, the operations which it allows itself to perform in the differential and integral calculus are in complete contradiction with the nature of merely finite determinations and their relations and would therefore have to be justified solely by the Notion.
§ 573
Although the mathematics of the infinite maintained that these quantitative determinations are vanishing magnitudes, i.e. magnitudes which are no longer any particular quantum and yet are not nothing but are still a determinateness relatively to an other, it seemed perfectly clear that such an intermediate state, as it was called, between being and nothing does not exist. What we are to think of this objection and the so-called intermediate state, has already been indicated above in Remark 4 to the category of becoming. The unity of being and nothing is, of course, not a state; a state would be a determination of being and nothing into which these moments might be supposed to have lapsed only by accident, as it were, into a diseased condition externally induced through erroneous thinking; on the contrary, this mean and unity, the vanishing or equally the becoming is alone their truth.
§ 574
Further, it has been said that what is infinite is not comparable as something greater or smaller; therefore there cannot be a relation between infinites according to orders or dignities of the infinite, although in the science of infinitesimals these distinctions do occur. Underlying this objection already mentioned is always the idea that here we are supposed to be dealing with quanta which are compared as quanta, that determinations which are no longer quanta no longer have any relationship to each other. But the truth is rather that that which has being solely in the ratio is not a quantum; the nature of quantum is such that it is supposed to have a completely indifferent existence apart from its ratio, and its difference from another quantum is supposed not to concern its own determination; on the other hand the qualitative is what it is only in its distinction from an other. The said infinite magnitudes, therefore, are not merely comparable, but they exist only as moments of comparison, i.e. of the ratio.
§ 575
I will adduce the most important definitions of this infinite which have been given in mathematics. From these it will be clear that the thought underlying them accords with the Notion developed here, but that the originators of the definitions did not establish the thought as Notion and found it necessary in the application to resort again to expedients which conflict with their better cause.
§ 576
The thought cannot be more correctly determined than in the way Newton has stated it. I eliminate here those determinations which belong to the idea of motion and velocity (from which, mainly, he took the name of fluxions) because in them the thought does not appear in its proper abstraction but as concrete and mixed with non-essential forms. Newton explains that he understands by these fluxions not indivisibles (a form which was used by earlier mathematicians, Cavalieri and others and which involves the concept of an intrinsically determinate quantum), but vanishing divisibles; also not sums and ratios of determinate parts but the limits (limites) of sums and ratios. It may be objected that vanishing magnitudes do not have a final ratio, because the ratio before it vanishes is not final, and when it has vanished is no longer a ratio. But by the ratio of vanishing magnitudes is to be understood not the ratio before which and after which they vanish, but with which they vanish. (quacum evanescunt). Similarly, the first ratio of nascent magnitudes is that with which they become.
§ 577
Newton did what the scientific method of his time demanded, he only explained what was to be understood by an expression; but that such and such is to be understood by it is, properly speaking, a subjective presumption, or a historical demand, without any indication that such a concept is in itself absolutely necessary or that there is truth in it. However, what has been quoted shows that the concept put forward by Newton corresponds to the way in which infinite quantity resulted from the reflection of quantum into itself in the exposition above. By magnitudes is understood magnitudes in their vanishing, i.e. which are no longer quanta; also, not ratios of determinate parts, but the limits of the ratio. The meaning is, therefore, that with the vanishing of the quanta individually, the sides of the ratio, there also vanishes the ratio itself in so far as it is a quantum; the limit of the quantitative ratio is that in which it both is and is not, or, more precisely, in which the quantum has vanished, with the result that the ratio and its sides are preserved, the former only as a qualitative relation of quantity and the latter similarly as qualitative moments of quantity. Newton goes on to add that from the fact that there are final ratios of vanishing magnitudes, it must not be inferred that there are final magnitudes, indivisibles. For this would mean a leap again from the abstract ratio to its sides as supposedly having an independent value of their own as indivisibles outside their relation, as something which would be a one, something devoid of any relation at all.
§ 578
To prevent such a misunderstanding, he again points out that final ratios are not ratios of final magnitudes, but are limits to which the ratios of the magnitudes decreasing without limit are nearer than any given, i.e. finite, difference; the ratios, however, do not exceed these limits, for if they did they would become nullities. In other words, final magnitudescould have been taken to mean, as already said, indivisibles or ones. But the definition of the final ratio excludes the conception both of the indifferent one which is devoid of any relation, and of the finite quantum. If the required determination had been developed into the Notion of a quantitative determination which is purely a moment of the ratio, there would have been no need for the decreasing without limit into which Newton converts the quantum and which only expresses the progress to infinity, or for the determination of divisibility which no longer has any immediate meaning here.
§ 579
As regards the preservation of the ratio in the vanishing of the quanta, there is found elsewhere, as in Carnot, the expression that by virtue of the law of continuity, the vanishing magnitudes still retain the ratio from which they come, before they vanish.
§ 580
This conception expresses the true nature of the matter, if the continuity of the quantum is not understood to be the continuity which it has in the infinite progress where the quantum is continued in its vanishing in such a manner that in itsbeyond there arises only a finite quantum again, only a fresh term of the series; but a continuous progress is always imagined as one in which values are passed through, values which are still finite quanta. On the other hand, where the transition is made into the true infinite it is the ratio that is continuous; so continuous is it, so completely is it preserved, that the transition may be said to consist solely in throwing into relief the pure ratio and causing the non-relational determination — i.e. that a quantum which is a side of the ratio is still a quantum outside this relation — to vanish. This purification of the quantitative ratio is thus analogous to grasping an empirical reality in terms of its Notion. The empirical reality is thereby raised above itself in such a way that its Notion contains the same characteristic features as it has itself, but these are grasped in their essentiality and are taken into the unity of the Notion in which they have lost their indifferent, Notion — less existence.
§ 581
The other form of Newton's exposition of the magnitudes in question is equally interesting, namely, as generative magnitudes or principles. A generated magnitude (genita) is a product or quotient, such as a root, rectangle, square, also the sides of rectangles and squares — in general, a finite magnitude. 'Such a magnitude being considered as variable, increasing or decreasing in ceaseless motion and flux, he gives its momentary increments or decrements the name of moments. But these are not to be taken for particles of a definite magnitude (particulae finitae): such would not themselves be moments but magnitudes generated from moments. Rather are they to be understood as the nascent principles or beginnings of finite magnitudes.' Here the quantum is distinguished from itself: as a product or a real being [Daseiendes], and in its becoming (or as nascent), in its beginning and principle, that is to say, in its Notion, or, what is here the same thing, in its qualitative determination: in the latter the quantitative differences, the infinite increments or decrements, are only moments; only that which has becoming at its back has passed over into the indifference of determinate being and into externality, i.e. is quantum. But if on the one hand the philosophy of the true Notion must acknowledge these determinations of the infinite with respect to increments or decrements, on the other hand it must be observed that the very forms of increments etc. fallwithin the category of immediate quantum and of the continuous progress to which we have referred; in fact the conceptions of increment, growth or increase of x by dx or i, and so on, are to be regarded as the fundamental vice in these methods — the permanent obstacle to disengaging the determination of the qualitative moment of quantity in its purity from the conception of the ordinary quantum.
§ 582
The conception of infinitesimals which is implicit, too, in the increment or decrement itself, is much inferior to the above determinations. The nature of these magnitudes is supposed to be such that they may be neglected, not only in comparison with finite magnitudes, but also their higher orders in comparison with their lower, and even the products of several in comparison with a single one. With Leibniz, this demand to neglect is more strikingly prominent than with previous inventors of methods relating to these infinitesimals in which this call to neglect also occurs. It is chiefly this call to neglect which, along with a gain in facility, has given this calculus the appearance of inexactitude and express incorrectness in its method of procedure. Wolf has tried to make this neglect intelligible in his own way of popularising things, i.e. by polluting the pure Notion and setting in its place incorrect sensuous conceptions. For example, he compares the neglect of infinitesimals of higher orders relatively to lower with the procedure of a surveyor who, in measuring the height of a mountain is no less accurate if meanwhile the wind has blown away a grain of sand from the top; or with the neglect of the height of houses or towers when calculating lunar eclipses.
§ 583
Even if ordinary common sense in fairness allows such inexactitude, all geometricians reject this conception. It is quite obvious that in the science of mathematics there cannot be any question of such empirical accuracy; mathematical measuring by operations of the calculus or by geometrical constructions and proofs is altogether different from land-surveying, from the measuring of empirical lines, figures etc. Besides, by comparing the result obtained by a strictly geometrical method with that obtained by the method of infinite differences, analysts demonstrate that the one is the same as the other and that there is absolutely no question of a greater or lesser degree of exactness. And it is self-evident that an absolutely exact result could not emerge from an inexact method. Yet on the other hand again, the method itself cannot do without this omission of what is regarded as insignificant, despite its protestations against the way this omission is justified. And this is the difficulty which engages the efforts of the analysts to make intelligible and to remove the inherent inconsistency.
§ 584
It is especially Euler's conception of the matter which must be cited here. He adopts the general Newtonian definition and insists that the differential calculus considers the ratios of the increments of a magnitude, but that the infinite differenceas such is to be considered as wholly nil. How this is to be understood is clear from the foregoing; the infinite difference is a nil only of quantum, not a qualitative nil, but as a nil of quantum it is a pure moment of the ratio only. It is not a quantitativedifference; but for that reason it is, on the one hand, altogether wrong to speak of those moments which are called infinitesimals, also as increments or decrements and as differences. This description implies that something is added to or subtracted from the initially given finite magnitude, that a subtraction or addition, an arithmetical, external operation takes place. But it is to be noticed that the transition of the function of the variable magnitude into its differential is of a quite different nature; as we have made clear, it is to be considered as a reduction of the finite function to the qualitative relation of its quantitative determinations. On the other hand, the error becomes obvious when it is said that the increments by themselves are zeros, that only their ratios are considered; for a zero no longer has any determinateness at all. This conception then, does get as far as the negative of the quantum and gives definite expression to it, but at the same time it does not grasp this negative in its positive significance of qualitative determinations of quantity which, if they were torn out of the ratio and regarded as quanta, would be only zeros.
§ 585
The opinion of Lagrange on the idea of limits or final ratios is that although one can well imagine the ratio of two magnitudes so long as they remain finite, this ratio does not present any clear and definite concept to the intellect as soon as its terms become simultaneously zero. And the understanding must, indeed, transcend this merely negative side on which the terms of the ratio are quantitatively zero, and must grasp them positively, as qualitative moments. But we cannot regard, as satisfactory Euler's further remarks with regard to this conception of his in which he tries to show that two so-called infinitesimals which are supposed to be nothing else but zeros, nevertheless stand in a relation to each other, for which reason they are denoted by symbols other than zero. He tries to base this on the difference between the arithmetical and geometrical ratio: in the former, we have an eye to the difference, in the latter, to the quotient, so that although in the former there is no difference between two zeros, this is not so in the geometrical ratio; if 2: 1 = 0 : 0 then from the nature of proportion it follows that, because the first term is twice as great as the second, the third is also twice as great as the fourth; thus according to proportion, 0 : 0 is to be taken as the ratio of 2 : 1. Even in common arithmetic n. 0 = 0 and therefore n : 1 = 0 : 0. But it is just because 2 : 1 or n : 1 is a relation of quanta that there cannot be any corresponding ratio or expression of 0 : 0.
§ 586
I refrain from citing any further instances since those already considered show clearly enough that the genuine Notion of the infinite is, in fact, implied in them, but that the specific nature of that Notion has not been brought to notice and grasped. Consequently, in the actual application of the method of infinitesimals, the genuine Notion of the infinite cannot exercise any influence; on the contrary, there is a return of the finite determinateness of quantity and the operation cannot dispense with the conception of a quantum which is merely relatively small. The calculus makes it necessary to subject the so-called infinitesimals to ordinary arithmetical operations of addition and so on, which are based on the nature of finite magnitudes, and therefore to regard them momentarily as finite magnitudes and to treat them as such. It is for the calculus to justify its procedure in which it first brings them down into this sphere and treats them as increments or differences, and then neglects them as quanta after it had just applied forms and laws of finite magnitudes to them.
I will proceed to cite the main features of the attempts of the geometricians to remove these difficulties.
§ 587
The older analysts had little scruples in the matter, but the moderns directed their efforts mainly towards bringing the differential calculus back to the evidence of a strictly geometrical method and in it to attain to the rigour of the proofs of the ancients (Lagrange's expressions) in mathematics. But since the principle of infinitesimal analysis is of a higher nature than the principle of the mathematics of finite magnitudes, that kind of evidence had perforce to be dispensed with, just as philosophy, too, cannot lay claim to that obviousness which belongs to the natural sciences, e.g. natural history — and just as eating and drinking are reckoned a more intelligible business than thinking and understanding. Accordingly, we shall deal only with the efforts to attain to the rigour of proof of the ancients.
§ 588
Some have attempted to dispense altogether with the concept of the infinite, and without it to achieve what seemed to be bound up with its use. Lagrange speaks, e.g., of the method devised by Landen, saying that it is purely analytical and does not employ infinitesimal differences, but starts with different values of variable magnitudes and subsequently equates them. He also gives it as his opinion that in this method, the differential calculus loses its own peculiar advantages, namely simplicity of method and facility of operation. This is, indeed, a procedure which in some measure corresponds to the starting-point of Descartes' tangential method of which detailed mention will be made later. This much, we may remark here, is generally evident, that the general procedure in which different values of variable magnitudes are assumed and subsequently equated, belongs to another department of mathematical treatment than that to which the method of the differential calculus itself belongs; and that the peculiar nature of the simple relation (to be considered in detail further on) to which its actual, concrete determination reduces, namely, of the derived function to the original, is not brought into prominence.
§ 589
The earlier of the moderns, Fermat, Barrow, and others for example, who at first used infinitesimals in that application which was subsequently developed into the differential and integral calculus, and then Leibniz, too, and those following him including Euler, always frankly believed that they were entitled to omit the products of infinitesimal differences and their higher powers, solely on the ground that they vanish relatively to the lower order. This is for them the sole basis of the fundamental principle, namely the determination of that which is the differential of a product or a power, for the entire theoretical teaching reduces to this. The rest is partly the mechanism of development and partly application, in which however as we shall later on see, the more important, or rather the sole, interest is to be found. With respect to the present topic, we need only mention here what is elementary, that on the same ground of insignificance, the cardinal principle adopted in relation to curves is that the elements of the curves, namely the increments of abscissa and ordinate, have therelation to each other of subtangent and ordinate; for the purpose of obtaining similar triangles, the arc which forms the third side of a triangle to the two increments of the characteristic triangle (as it rightly used to be called), is regarded as a straight line, as part of the tangent and one of the increments therefore as reaching to the tangent. By these assumptions those determinations are, on the one hand, raised above the nature of finite magnitudes, but on the other hand, a method which is valid only for finite magnitudes and which does not permit the omission of anything on the ground of insignificance, is applied to moments now called infinitesimal. With such a mode of procedure, the difficulty which encumbers the method remains in all its starkness.
§ 590
We must mention here a remarkable procedure of Newton the invention of an ingenious device to remove the arithmetically incorrect omission of the products of infinitesimal differences or higher orders of them in the finding of differentials. He finds the differentials of products — from which the differentials of quotients, powers, etc., can then be easily derived — in the following way. The product of x and y, when each is taken as reduced by half of its infinitesimal difference, becomes xy -xdy/2 - ydx/2 + dxdy/4; but if x and y are made to increase by the same amount, it becomes xy + xdy/2 + ydx/2 +dxdy/4. Now when the first product is subtracted from the second, ydx + xdy remains as a surplus and this is said to be the surplus of the increase by a whole dx and dy, for this increase is the difference between the two products; it is therefore the differential of xy. Clearly, in this procedure, the term which forms the chief difficulty, the product of the two infinitesimal differences, cancels itself out. But in spite of the name of Newton it must be said that such an operation although very elementary, is incorrect; it is not true that (x + dx/2) (y + dy/2) - (x - dx/2) (y - dy/2) = (x + dx) (y + dy) - xy. It can only have been the need to establish the all-important fluxional calculus which could bring a Newton to deceive himself with such a proof.
§ 591
Other forms which Newton employed in the derivation of differentials are bound up with concrete meanings of the elements and their powers, meanings relating to motion. About the use of the serial form which also characterises his method, it suggests itself to say that it is always possible to obtain the required degree of accuracy by adding more terms and that the omitted terms are relatively insignificant, in general, that the result is only an approximation; though here too he would have been satisfied with this ground for omission as he is in his method of solving equations of higher degree by approximation, where the higher powers arising from the substitution in the given equation of any ascertained, still inexact term, are omitted on the crude ground of their relative smallness.'
§ 592
The error into which Newton fell in solving a problem by omitting essential, higher powers, an error which gave his opponents the occasion of a triumph of their method over his, and the true origin of which has been indicated by Lagrange in his recent investigation of it demonstrates the formalism and uncertainty which still prevailed in the use of this instrument. Lagrange shows that Newton made the mistake because he omitted the term of the series containing that power on which the specific problem turned. Newton had kept to the formal, superficial principle of omitting terms on account of their relative smallness. For example, it is well known that in mechanics the terms of the series in which the function of a motion is developed are given a specific meaning, so that the first term or the first function refers to the moment of velocity, the second to the accelerating force and the third to the resistance of forces. Here, then, the terms of the series are not to be regarded merely as parts of a sum, but rather as qualitative moments Of a whole determined by the concept. In this way, the omission of the rest of the terms belonging to the spuriously infinite series acquires an altogether different meaning from omission on the ground of their relative smallness.
[Both considerations are found set simply side by side in the application by Lagrange of the theory of functions to mechanics in the chapter on rectilinear motion The space passed through, considered as a function of the time elapsed, gives the equation x = ft; this, developed as f(t + d) gives ft + df't + d2/2.f"t + , etc.
Thus the space traversed in the period of time is represented in the formula as = df't + d2f"t + d3/2.3f"'t +, etc. The motion by means of which this space has been traversed is (it is said) therefore — i.e. because the analytical development gives several, in fact infinitely, many terms — composed of various partial motions, of which the spaces corresponding to the time will be df't, d2/2f"t, d3/2.3f"'dt, etc. The first partial — notion is, in known motion, the formally uniform one with a velocity designated by f't, the second is uniformly accelerated motion derived from an accelerative force proportional to f"t. Now since the remaining terms do not refer to any simple known motion, it is not necessary to take them specially into account and we shall show that they may be abstracted from in determining the motion at the beginning of the point of time.' This is now shown, but of course only by comparingthe series all of whose terms belonged to the determination of the magnitude of the space traversed in the period of time, with the equation given in art. 3 for the motion of a falling body, namely x = at + bt2 in which only these two terms occur. But this equation has itself received this form only because the explanation given to the terms produced by the analytical development is presupposed; this presupposition is that the uniformly accelerated motion is composed of a formally uniform motion continued with the velocity attained in the preceding period of time, and of an increment (the a in s = at2, i.e. the empirical coefficient) which is ascribed to the force of gravity — a distinction which has no existence or basis whatever in the nature of the thing itself, but is only the falsely physicalised expression of what issues from the assumed analytical treatment.]
The error in the Newtonian solution arose, not because terms of the series were neglected only as parts of a sum, but because the term containing the qualitative determination, which is the essential point, was ignored.
§ 593
In this example, the procedure is made to depend on the qualitative meaning. In this connection the general assertion can at once be made that the whole difficulty of the principle would be removed if the qualitative meaning of the principle were stated and the operation were made to depend on it — in place of the formalism which links the determination of the differential only to that which gives the problem its name, to the difference as such between a function and its variation after its variable magnitude has received an increment. In this sense, it is obvious that the differential of xn is completely exhausted by the first term of the series which results from the expansion of (x + dx)n . Thus the omission of the rest of the terms is not on account of their relative smallness; and so there is no assumption of an inexactitude, an error or mistake which could be compensated or rectified by another error — a point of view from which Carnot in particular justifies the ordinary method of the infinitesimal calculus. Since what is involved is not a sum but a relation, the differential is completely given by the first term; and where further terms, the differentials of higher orders, are required, their determination involves not the continuation of a series as a sum, but the repetition of one and the same relation which alone is desired and which is thus already completely given in the first term. The need for the form of a series, its summation and all that is connected with it, must then be wholly separated from the said interest of the relation.
§ 594
The explanations of the methods of infinitesimal magnitudes given by Carnot, contain a most lucid exposition of what is essential in the ideas referred to above. But in passing to the practical application itself, there enter more or less the usual ideas about the infinite smallness of the omitted terms relatively to the others. He justifies the method, not by the nature of the procedure itself, but by the fact that the results are correct, and by the advantages of a simplification and shortening of the calculus which follow the introduction of imperfect equations, as he calls them, i.e. those in which such an arithmetically incorrect omission has occurred.
§ 595
Lagrange, as is well known, reverted to Newton's original method, that of series, in order to be relieved of the difficulties inherent in the idea of the infinitely small and in the method of first and final ratios and limits. The advantages of his functional calculus as regards precision, abstraction and generality, are sufficiently recognised; we need mention only what is pertinent here, that it rests on the fundamental principle that the difference, without becoming zero, can be assumed so small that each term of the series is greater than the sum of all the following terms. This method, too, starts from the categories ofincrement and difference of the function, the variable magnitude of which receives the increment, thereby bringing in the troublesome series of the original function; also in the sequel the terms to be omitted are considered only as constituting a sum, while the reason for omitting them is made to consist in the relativity of their quantum. And so here, too, on the one hand, the principle of the omission is not brought back to the point of view exemplified in some applications, where (as was remarked above) terms of the series are supposed to have a specific quality significance, and terms are neglected not because of their quantitative insignificance but because they are not qualitatively significant; and then, on the other hand, the omission itself has no place in the essential point of view which, as regards the so-called differential coefficient, only becomes specifically prominent with Lagrange, in the so-called application of the calculus, as will be more fully considered in the following remark.
§ 596
The demonstrated qualitative character as such of the form of magnitude here under discussion in what is called the infinitesimal, is found most directly in the category of limit of the ratio referred to above and the carrying out of which in the calculus has been developed into a characteristic method. Lagrange criticises this method as lacking case in application and he claims that the expression limit does not present any definite idea; this second point we will take up here and examine more closely what is stated about its analytical meaning. Now the idea of limit does indeed imply the true category of the qualitatively determined relation of variable magnitudes above-mentioned; for the forms of it which occur, dx anddy, are supposed to be taken simply and solely as moments of dy/dx, and dy/dx itself must be regarded as a single indivisible symbol.
§ 597
That the mechanism of the calculus, especially in its application, thus loses the advantage it derived from the separation of the sides of the differential coefficient, this we will pass over here. Now the said limit is to be limit of a given function; it is to assign to this function a certain value determined by its mode of derivation. But with the mere category of limit we should not have advanced beyond the scope of this Remark, which is to demonstrate that the infinitely small which presents itself in the differential calculus as dx and dy, does not have merely the negative, empty meaning of a non-finite, non-given magnitude, as when one speaks of 'an infinite multitude', 'to infinity', and the like, but on the contrary has the specific meaning of the qualitative nature of what is quantitative, of a moment of a ratio as such. This category, however, merely as such, still has no relation to that which is a given function and does not itself enter into the treatment of such a function or into the use to be made of that determination; thus the idea of limit, too, confined to this its demonstrated character, would lead nowhere. But the very expression 'limit' implies that it is a limit of something, i.e. that it expresses a certain value which lies in the function of a variable magnitude; and we must examine the nature of this concrete role. It is supposed to be the limit of the ratio between the two increments by which the two variable magnitudes connected in an equation (one of which is regarded as a function of the other), are supposed to have been increased; the increase is taken here as quite undetermined and so far no use is made of the infinitely small. But the way in which this limit is found involves the same inconsistencies as are contained in the other methods. This way is as follows: if y = fx, then when y becomes y + k, fx is to change into fx + ph + qh2 + rh3 and so on; thus k = ph + qh2, etc., and k/h = p + qh + rh2, etc. Now if k andh vanish, the right-hand side of the equation also vanishes with the exception of p; now p is supposed to be the limit of the ratio of the two increments. It is clear that while h, as a quantum, is equated with 0, k/h nevertheless is not at the same time equal to 0/0 but is supposed still to remain a ratio.
§ 598
Now the idea of limit is supposed to have the advantage of avoiding the inconsistency here involved; p is, at the same time, supposed to be not the actual ratio, which would be 0/0 but only that specific value to which the ratio can infinitely approximate, i.e. can approach so near that the difference can be smaller than any given difference. The more precise meaning of approximation with respect to the terms which are supposed really to approach each other will be considered later. But that a quantitative difference, the definition of which is that it not only can, but shall be smaller than any given difference, is no longer a quantitative difference, this is self-evident, as self-evident as anything can be in mathematics; but we still have not got away from dy/dx = 0. If on the other hand dy/dx = p, i. e. is assumed to be a definite quantitative ratio as in fact it is, then conversely there is a difficulty about the presupposition which equates h with o, a presupposition which is indispensable for obtaining the equation k/h = p. But if it be granted that k/h = 0, (and when h = 0, k is in fact automatically = 0, for k, the increment of y, depends entirely on the existence of the increment h), then the question would arise, what p — which is a quite definite quantitative value — is supposed to be. To this there is at once an obvious answer, the simple, meagre answer that it is a coefficient derived in such and such a way — the first function, derived in a certain specific manner, of an original function. if we content ourselves with this — and Lagrange did, in fact, do so in practice — then the general part of the science of the differential calculus, and straightway this one particular form of it called the theory of limits would be rid of the increments and of their infinite or arbitrary smallness — spared too, the difficulty of getting rid again of all the terms of a series other than the first, or rather only the coefficient of the first, which inevitably follow on the introduction of these increments; in addition it would also be purged of those formal categories connected with them, especially of the infinite, of infinite approximation and, too, the categories, here equally empty, of continuous magnitude' which, moreover, like nisus, becoming, occasion of a variation, are deemed necessary.
§ 599
[The category of continuous or fluent magnitude enters with the consideration of the external and empirical variation of magnitudes — which are brought by an equation into the relation in which one is a function of the other; but since the scientific object of the differential calculus is a certain relation (usually expressed by the differential coefficient), the specific nature of which may equally well be called a law, the mere continuity is a heterogeneous aspect of this specific nature, and besides is in any case an abstract and here empty category seeing that nothing whatever is said about the law of continuity. Into what formal definitions one may be led in these matters can be seen from the penetrating exposition by my respected colleague, Prof. Dirksen of the fundamental determinations used in the deduction of the differential calculus, which forms an appendix to the criticism of some recent works on this science. The following definition is actually quoted: 'A continuous magnitude, a continuum, is any magnitude thought of as in a state of becoming such that this becoming takes place not by leaps but by an uninterrupted progress'. This is surely tautologically the same as what was to be defined.]
§ 600
But it would then be required to show what other meaning and value p has — apart from the meagre definition, quite adequate for the theory, that it is simply a function derived from the expansion of a binomial — i.e. what relationships it embodies and what further use can be made of them mathematically; this will be the subject of Remark 2. But first we shall proceed to discuss the confusion which the conception of approximation currently used in expositions of the calculus, has occasioned in the understanding of the true, qualitative determinateness of the relation which was the primary interest concerned.
§ 601
It has been shown that the so-called infinitesimals express the vanishing of the sides of the ratio as quanta, and that what remains is their quantitative relation solely as qualitatively determined; far from this resulting in the loss of the qualitative relation, the fact is that it is just this relation which results from the conversion of finite into infinite magnitudes. As we have seen, it is in this that the entire nature of the matter consists. Thus in the final ratio, for example, the quanta of abscissa and ordinate vanish; but the sides of this ratio essentially remain, the one an element of the ordinate, the other an element of the abscissa. This vanishing being represented as ' an infinite approximation, the previously distinguished ordinate is made to pass over into the other ordinate, and the previously distinguished abscissa into the other abscissa; but essentially this is not so, the ordinate does not pass over into the abscissa, neither does the abscissa pass into the ordinate. To continue with this example of variable magnitudes, the element of the ordinate is not to be taken as the difference of one ordinate from another ordinate, but rather as the difference or qualitative determination of magnitude relatively to the element o the abscissa; the principle of the one variable magnitude relatively to that of the other is in reciprocal relation with it. The difference, as no longer a difference of finite magnitudes, has ceased to be manifold within itself; it has collapsed into a simple intensity, into the determinateness of one qualitative moment of a ratio relatively to the other.
§ 602
This is the nature of the matter but it is obscured by the fact that what has just been called an element, for example, of the ordinate, is grasped as a difference or increment in such a way that it is only the difference between the quantum of one ordinate and the quantum of another ordinate. And so the limit here does not have the meaning of ratio; it counts only as the final value to which another magnitude of a similar kind continually approximates in such a manner that it can differ from it by as little as we please, and that the final ratio is a ratio of equality. The infinite difference is thus the fluctuation of a difference of one quantum from another quantum, and the qualitative nature according to which dx is essentially not a determination of the ratio relatively to x, but to dy, comes to be overlooked. Dx is permitted to vanish relatively to dx, but even more does dx vanish relatively to x; but this means in truth: it has a relation only to dy. In such expositions, geometricians are mainly concerned to make intelligible the approximation of a magnitude to its limit and to keep to this aspect of the difference of quantum from quantum, how it is no difference and yet still is a difference. But all the same, approximation is a category which of itself says nothing and explains nothing; dx already has approximation behind it; it is neither near nor nearer; and 'infinitely near', itself means the negation of nearness and approximation.
§ 603
Now since this implies that the increments or infinitesimals have been considered only from the side of the quantum which vanishes in them, and only as a limit, it follows that they are grasped as unrelated moments. From this would follow the inadmissible idea that it is allowed in the final ratio to equate, say abscissa and ordinate, or even sine, cosine, tangent, versed sine, and what not. This idea seems at first to prevail when the arc is treated as a tangent; for the arc, too, is certainly incommensurable with the straight line, and its element is, in the first place, of another quality than the element of the straight line. It seems even more absurd and inadmissible than the confusing of abscissa, ordinate, versed sine, cosine, etc., when quadrata rotundas, when part of an arc, even though an infinitely small part, is taken to be a part of the tangent and so treated as a straight line. However, this treatment differs essentially from the confusion we have decried; it is justified by the circumstance that in the triangle which has for its sides the element of an arc and the elements of its abscissa and ordinate, the relation is the same as if this element of the arc were the element of a straight line, of the tangent; theangles which constitute the essential relation, i.e. that which remains to these elements when abstraction is made from the finite magnitudes belonging to them, are the same. This can also be expressed as the transition of straight lines which are infinitely small, into curved lines, and their relation in their infinity as a relation of curves. Since, according to its definition, a straight line is the shortest distance between two points, its difference from the curved line is based on the determination ofamount, on the smaller amount of what is differentiated in this manner, a determination, therefore, of a quantum. But this determination vanishes in the line when it is taken as an intensive magnitude, as an infinite moment, as an element, and with it, too, its difference from the curved line which rested merely on the difference of quantum. As infinite, therefore, the straight line and arc no longer retain any quantitative relation nor consequently, on the basis of the assumed definition, any qualitative difference from each other either; on the contrary, the former passes into the latter.
§ 604
Analogous, although also distinct from, the equating of heterogeneous forms is the assumption that infinitely small partsof the same whole are equal to each other; an assumption in itself indefinite and completely indifferent, but which, applied to an object heterogeneous within itself, i.e. an object whose quantitative determination is essentially non-uniform, produces the peculiar inversion contained in that proposition of higher mechanics which states that infinitely small parts of a curve are traversed in equal, infinitely small times in a uniform motion, inasmuch as this is asserted of a motion in which in equal finite, i.e. existent, parts of time, finite, i.e. existent, unequal parts of the curve are traversed, of a motion therefore which exists as non-uniform and is assumed as such. This proposition is the expression in words of what is supposed to be the significance of an analytical term obtained in the above-mentioned development of the formula relating to a motion which is non-uniform but otherwise conforms to a law. Earlier mathematicians sought to express in words and propositions and to exhibit in geometrical tables the results of the newly invented infinitesimal calculus (which moreover always had to do with concrete objects), chiefly in order to use them for theorems susceptible of the ordinary method of proof. The terms of a mathematical formula into which analytical treatment resolved the magnitude of the object, of motion, for instance, acquired there an objective significance, such as velocity, force of acceleration, and so on; in accordance with this meaning they were supposed to furnish correct propositions, physical laws; their objective connections and relations, too, were supposed to be determined in accordance with the analytical connection. A particular example is that in a uniformly accelerated motion there is supposed to exist a special velocity proportional to the times, but that to this velocity there constantly accrues an increment from the force of gravity.
§ 605
In the modern, analytical form of mechanics such propositions are put forward simply as results of the calculus, without enquiry whether by themselves and in themselves they have a real significance, i.e. one to which there is a corresponding physical existence and whether such meaning can be demonstrated. The difficulty of making intelligible the connection of such forms when they are taken in the real meaning alluded to, for example the transition from said simply uniform velocity to a uniformly accelerated velocity, is held to be completely eliminated by the analytical treatment in which such connection is a simple result of the authority now established once and for all of the operations of the calculus. It is announced as a triumph of science that by means of the calculus alone, laws are found transcending experience, that is, propositions about existence which have no existence. But in the earlier, still naive period of the infinitesimal calculus, the aim was to assign to those forms and propositions represented in geometrical diagrams a real meaning of their own and to make that meaning plausible, and to apply the forms and propositions bearing such meaning in the proof of the main propositions concerned.
§ 606
It cannot be denied that in this field much has been accepted as proof, especially with the aid of the nebulous conception of the infinitely small, for no other reason than that the result was always already known beforehand, and that the proof which was so arranged that the result did emerge, at least produced the illusion of a framework of proof, an illusion which was still preferred to mere belief or knowledge from experience. But 1 do not hesitate to regard this affectation as nothing more than mere jugglery and window-dressing, and I include in this description even Newton's proofs, especially those belonging to what has just been quoted, for which Newton has been extolled to the skies and exalted above Kepler, namely that he demonstrated mathematically what Kepler had discovered merely empirically.
§ 607
The empty scaffolding of such proofs was erected in order to prove physical laws. But mathematics is altogether incapable of proving quantitative determinations of the physical world in so far as they are laws based on the qualitative nature of the moments [of the subject matter]; and for this reason, that this science is not philosophy, does not start from the Notion, and therefore the qualitative element, in so far as it is not taken lemmatically from experience, lies outside its sphere. The desire to uphold the honour of mathematics, that all its propositions ought to be rigorously proved, has often caused it to forget its limits; thus it seemed against its honour to acknowledge simply experience as the source and sole proof of empirical propositions. Consciousness has since then developed a more instructed view of the matter; so long, however, as consciousness is not clearly aware of the distinction between what is mathematically demonstrable and what can come only from another source, between what are only terms of an analytical expansion and what are physical existences, scientific method cannot be developed into a rigorous and pure attitude in this field. Without doubt, however, the same justice will be done to that framework of Newtonian proof as was done to another baseless and artificial Newtonian structure of optical experiments and conclusions derived from them. Applied mathematics is still full of a similar concoction of experiment and reflection; but just as one part after another of Newtonian optics long since began to be ignored in practice by the science — with the inconsistency however that all the rest although in contradiction was allowed to stand — so, too, it is a fact that already some of those illusory proofs have fallen into oblivion or have been replaced by others.
Remark 2: The Purpose of the Differential Calculus Deduced from its Application
§ 608
In the previous Remark we considered on the one hand the specific nature of the notion of the infinitesimal which is used in the differential calculus, and on the other the basis of its introduction into the calculus; both are abstract determinations and therefore in themselves also easy. The so-called application, however, presents greater difficulties, but also the more interesting side; the elements of this concrete side are to be the object of this Remark. The whole method of the differential calculus is complete in the proposition that dxn = nx(n - 1)dx, or (f(x + i) - fx)/i = P, that is, is equal to the coefficientof the first term of the binomial x + d, or x + 1, developed according to the powers of dx or i. There is no need to learn anything further: the development of the next forms, of the differential of a product, of an exponential magnitude and so on, follows mechanically; in little time, in half an hour perhaps — for with the finding of the differential the converse the finding of the original function from the differential, or integration, is also given — one can be in possession of the whole theory. What takes longer is simply the effort to understand, to make intelligible, how it is that, after having so easily accomplishedthe first stage of the task, the finding of the said differential, analytically, i.e. purely arithmetically, by the expansion of the function of the variable after this has received the form of a binomial by the addition of an increment; how it is that thesecond stage can be correct, namely the omission of all the terms except the first, of the series arising from the expansion. If all that were required were only this coefficient, then with its determination all that concerns the theory would, as we have said, be settled and done with in less than half an hour and the omission of the further terms of the series (with the determination of the first function, the determination of the second, third, etc., is also accomplished) far from causing any difficulty, would not come into question since they are completely irrelevant.
§ 609
We may begin by remarking that the method of the differential calculus shows on the face of it that it was not invented and constructed for its own sake. Not only was it not invented for its own sake as another mode of analytical procedure; on the contrary, the arbitrary omission of terms arising from the expansion of a function is absolutely contrary to all mathematical principles, it being arbitrary in the sense that the whole of this development is nevertheless assumed to belong completelyto the matter in hand, this being regarded as the difference between the developed function of a variable (after this has been given the form of a binomial) and the original function. The need for such a mode of procedure and the lack of any internal justification at once suggest that the origin and foundation must lie elsewhere. It happens in other sciences too, that what is placed at the beginning of a science as its elements and from which the principles of the science are supposed to be derived is not self-evident, and that it is rather in the sequel that the raison d'étre and proof of those elements is to be found. The course of events in the history of the differential calculus makes it plain that the matter had its origin mainly in the various so-called tangential methods, in what could be considered ingenious devices; it was only later that mathematicians reflected on the nature of the method after it had been extended to other objects, and reduced it to abstract formulae which they then also attempted to raise to the status of principle.
§ 610
We have shown that the specific nature of the notion of the so-called infinitesimal is the qualitative nature of determinations of quantity which are related to each other primarily as quanta; to this was linked the empirical investigation aimed at demonstrating the presence of this specific nature in the existing descriptions and definitions of the infinitesimal in so far as this is taken as an infinitesimal difference and the like. This was done only in the interest of the abstract nature of the notion as such; the next question would be as to the nature of the transition from this to the mathematical formulation and application. To this end we must first pursue our examination of the theoretical side, the specific nature of the notion, which will not prove wholly unfruitful in itself; we must then consider the relation of the theoretical side to its application; and in both cases we must demonstrate, so far as it is relevant here, that the general conclusions are at the same time adequate to the purpose of the differential calculus and to the way in which the calculus brings about its results.
§ 611
First, it is to be remembered that the mathematical form of the determinateness of the notion under discussion has already been stated in passing. The specifically qualitative character of quantity is first indicated in the quantitative relation as such; but it was already asserted in anticipation when demonstrating the so-called kinds of reckoning (see the relative Remark), that it is the relation of powers (still to be dealt with in its proper place) in which number, through the equating of the moments of its Notion, unit and amount, is posited as returned into itself, thereby receiving into itself the moment of infinity, of being-for-self, i.e. of being self-determined. Thus, as we have already said, the express qualitative nature of quantity is essentially connected with the forms of powers, and since the specific interest of the differential calculus is to operate with qualitative forms of magnitude, its own peculiar subject matter must be the treatment of forms of powers, and the whole range of problems, and their solutions, show that the interest lies solely in the treatment of determinations of powers as such.
§ 612
This foundation is important and at once puts in the forefront something definite in place of the merely formal categories of variable, continuous or infinite magnitudes or even of functions generally; yet it is still too general, for other operations also have to do with determinations of powers. The raising to a power, extraction of a root, treatment of exponential magnitudes and logarithms, series, and equations of higher orders, the interest and concern of all these is solely with relations which are based on powers. Undoubtedly, these together constitute a system of the treatment of powers; but which of the various relations in which determinations of powers can be put is the peculiar interest and subject matter of the differential calculus, this is to be ascertained from the calculus itself, i.e. from its so-called applications. These are, in fact, the core of the whole business, the actual procedure in the mathematical solution of a certain group of problems; this procedure was earlier than the theory or general part and was later called application only with reference to the subsequently created theory, the aim of which was to draw up the general method of the procedure and, as well, to endow it with first principles, i.e. with a justification. We have shown in the preceding Remark the futility of the search for principles which would clarify the method as currently understood, principles which would really solve the contradiction revealed by the method instead of excusing it or covering it up merely by the insignificance of what is here to be omitted (but which really is required by mathematical procedure), or, by what amounts to the same thing, the possibility of infinite or arbitrary approximation and the like. If from the practical part of mathematics known as the differential calculus the general features of the method were to be abstracted in a manner different from that hitherto followed, then the said principles and the concern about them would also show themselves to be superfluous, just as they reveal themselves to be intrinsically false and permanently contradictory.
§ 613
If we investigate this peculiarity by simply taking up what we find in this part of mathematics, we find as its subject matter:
(a) Equations in which any number of magnitudes (here we can simply confine ourselves to two) are combined into a qualitative whole in such a way that first, these equations have their determinateness in empirical magnitudes which are their fixed limits, and also in the kind of connection they have with these limits and with each other as is generally the case in an equation; but since there is only one equation for both magnitudes (similarly, relatively more equations for more magnitudes, but always fewer than the number of magnitudes), these equations belong to the class of indeterminate equations; and secondly, that one aspect of the determinateness of these magnitudes is that they are — or at least one of them is present in the equation in a higher power than the first.
§ 614
Before proceeding further, there are one or two things to be noticed about this. The first is that the magnitudes, as described under the first of the above two headings, have simply and solely the character of variables such as occur in the problems of indeterminate analysis. Their value is undetermined, but if one of them does receive a completely determined value, i.e. a numerical value, from outside, then the other too, is determined, so that one is a function of the other. Therefore, in relation to the specific quantitative determinateness here in question, the categories of variable magnitudes, functions and the like are, as we have already said, merely formal, because they are still too general to contain that specific element on which the entire interest of the differential calculus is focused, or to permit of that element being explicated by analysis; they are in themselves simple, unimportant, easy determinations which are only made difficult by importing into them what they do not contain in order that this may then be derived from them — namely, the specific determination of the differential calculus. Then as regards the so-called constant, we can note that it is in the first place an indifferent empirical magnitude determining the variables only with respect to their empirical quantum as a limit of their minimum and maximum; but the nature of the connection between the constants and the variables is itself a significant factor in the nature of the particular function which these magnitudes are. Conversely, however, the constants themselves are also functions; in so far as a straight line, for example, has the meaning of being the parameter of a parabola, then this meaning is that it is the function y2/x2; and in the expansion of the binomial generally, the constant which is the coefficient of the first term of the development is the sum of the roots, the coefficient of the second is the sum of the products, in pairs, and so on; here, therefore, the constants are simply functions of the roots. Where, in the integral calculus, the constant is determined from the given formula, it is to that extent treated as a function of this. Further on we shall consider these coefficients in another character than that of functions, their meaning in the concrete object being the focus of the whole interest.
§ 615
Now the difference between variables as considered in the differential calculus, and in their character as factors in indeterminate problems, must be seen to consist in what has been said, namely, that at least one of those variables (or even all of them), is found in a power higher than the first; and here again it is a matter of indifference whether they are all of the same higher power or are of unequal powers; their specific indeterminateness which they have here consists solely in this, that in such a relation of powers they are functions of one another. The alteration of variables is in this wayqualitatively determined, and hence continuous, and this continuity, which again is itself only the purely formal category of an identity, of a determinateness which is preserved and remains self-same in the alteration, has here its determinate meaning, solely, that is, in the power-relation, which does not have a quantum for its exponent and which forms the non-quantitative, permanent determinateness of the ratio of the variables. For this reason it should be noted, in criticism of another formalism, that the first power is only a power in relation to higher powers; on its own, x is merely any indeterminate quantum. Thus there is no point in differentiating for their own sakes the equations y = ax + b (of the straight line), or s = ct (of the plain uniform velocity); if from y = ax, or even ax + b, we obtain a = dy/dx, or from s = ct, ds/dt = c, then a = y/x is equally the determination of the tangent, or s/t that of velocity simply as such. The latter is given the form of dy/dx in the context of what is said to be the development of the uniformly accelerated motion; but, as already remarked, the presence in the system of such a motion, of a moment of simple, merely uniform velocity, i.e. a velocity which is not determined by the higher power of one of the moments of the motion is itself an empty assumption based solely on the routine of the method. Since the method starts from the conception of the increment which the variable is supposed to acquire, then of course a variable which is only a function of the first power can also receive an increment; when now in order to find the differential we have to subtract the difference of the second equation thus produced from the given equation, the meaninglessness of the operation becomes apparent, for, as we have remarked, the equation for the so-called increments, both before and after the operation, is the same as for the variables themselves.
§ 616
(b) What has been said determines the nature of the equation which is to be treated; we have now to indicate what is the interest on which the treatment of the equation is focused. This consideration can yield only known results, in a form found especially in Lagrange's version; but I have made the exposition completely elementary in order to eliminate the heterogeneous determinations associated with it. The basis of treatment of an equation of this kind shows itself to be this, that the power is taken as being within itself a relation or a system of relations. We said above that power is number which has reached the stage where it determines its own alteration, where its moments of unit and amount are identical — as previously shown, completely identical first in the square, formally (which makes no difference here) in higher powers. Now power is number (magnitude as the more general term may be preferred, but it is in itself always number), and hence a plurality, and also is represented as a sum; it can therefore be directly analysed into an arbitrary amount of numbers which have no further determination relatively to one another or to their sum, other than that together they are equal to the sum. But the power can also be split into a sum of differences which are determined by the form of the power. If the power is taken as a sum, then its radical number, the root, is also taken as a sum, and arbitrarily after manifold divisions, which manifoldness, however, is the indifferent, empirically quantitative element. The sum which the root is supposed to be, when reduced to its simple determinateness, i.e. to its genuine universality, is the binomial; all further increase in the number of terms is a mere repetition of the same determination and therefore meaningless.
[It springs solely from the formalism of that generality to which analysis perforce lays claim when, instead of taking (a + b)n for the expansion of powers, it gives the expression the form of (a + b + c + d...)n as happens too in many other cases; such a form is to be regarded as, so to speak, a mere affectation of a show of generality; the matter itself is exhausted in the binomial. It is through the expansion of the binomial that the law is found, and it is the law which is the genuine universality, not the external, mere repetition of the law which is all that is effected by this a + b + c + d ...]
§ 617
The sole point of importance here is the qualitative determinateness of the terms resulting from the raising to a powerof the root taken as a sum, and this determinateness lies solely in the alteration which the potentiation is. These terms, then, are wholly functions of potentiation and of the power. Now this representation of number as a sum of a plurality of terms which are functions of potentiation, and the finding of the form of such functions and also this sum from the plurality of those terms, in so far as this must depend solely on that form, this constitutes, as we know, the special theory of series.But in this connection it is essential to distinguish another object of interest, namely the relation of the fundamental magnitude itself (whose determinateness, since it is a complex, i.e. here an equation, includes within itself a power) tothe functions of its potentiation. This relation, taken in complete abstraction from the previously mentioned interest of the sum, will show itself to be the sole standpoint yielded by the practical aspect of the science.
§ 618
But first, another determination must be added to what has been said, or rather, one which is implied in it must be removed. It was said that the variable into the determination of which power enters is regarded as within itself a sum, in fact a system of terms in so far as these are functions of the potentiation, and that thus the root, too, is regarded as a sum and in the simply determined form of a binomial: xn = (y + z)n = (yn + ny(n-1)z + ... ). This exposition started from the sum as such for the expansion of the power, i.e. for obtaining the functions of its potentiation; but what is concerned here is not a sum as such, or the series arising from it; what is to be taken up from the sum is only the relation. The relation as such of the magnitudes is, on the one hand, all that remains after abstraction is made from the plus of a sum as such, and on the other hand, all that is needed for finding the functions produced by the expansion of the power.
§ 619
But such relation is already determined by the fact that here the object is an equation, ym = axn, and so already a complexof several (variable) magnitudes which contains a power determination of them. In this complex, each of these variables is posited simply as in relation to the others with the meaning, one could say, of a plus implicit in it — as a function of the other variables; their character, that of being functions of one another, gives them this determination of a plus which, however, for that same reason, is wholly indeterminate — not an increase or an increment, or anything of that nature. Yet even this abstract point of view we could leave out of account; we can quite simply stop at the point where the variables in the equation having received the form of functions of one another, such functions containing a relation of powers, the functions of potentiation are then also compared with one another — these second functions being determined simply and solely by the potentiation itself. To treat an equation of the powers of its variables as a relation of the functions developed by potentiation can, in the first place, be said to be just a matter of choice or a possibility; the utility of such a transformation has to be indicated by some further purpose or use; and the sole reason for the transformation was its utility.
§ 620
When we started above from the representation of these functions of potentiation of a variable which is taken as a sum complex within itself, this served only partly to indicate the nature of such functions, but partly also to show the way in which they are found.
§ 621
What we have here then is the ordinary analytical development which for the purpose of the differential calculus is operated in this way, that an increment dx or i is given to the variable and then the power of the binomial is developed by the terms of the series belonging to it. But the so-called increment is supposed to be not a quantum but only a form, the whole value of which is that it assists the development; it is admitted — most categorically by Euler and Lagrange and in the previously mentioned conception of limit — that what is wanted is only the resulting power determinations of the variables, the so-called coefficients, namely, of the increment and its powers, according to which the series is ordered and to which the different coefficients belong. On this we could perhaps remark that since an increment (which has no quantum) is assumed only for the sake of the development, it would be most appropriate to take i (the one) for that purpose, for in the development this always occurs only as a factor; the factor one, therefore, fulfils the purpose, namely, that the increment is not to involve any quantitative determinateness or alteration; on the other hand, dx, which is burdened with the false idea of a quantitative difference, and other symbols like i with the mere show — pointless here — of generality, always have the appearance and pretension of a quantum and its powers; which pretension then involves the trouble that they must nevertheless be removed and left out. In order to retain the form of a series expanded on the basis of powers, the designations of the exponents as indices could equally well be attached to the one. But in any case, abstraction must be made from the series and from the determination of the coefficients according to their place in the series; the relation between all of them is the same; the second function is derived from the first in exactly the same manner as this is from the original function, and for the function counted as second, the first derived function is itself original. But the essential point of interest is not the series but simply and solely the determination of the power resulting from the expansion in its relation to the variable which for the power determination is immediate. It should not therefore be defined as the coefficient of the first term of the development, for it is first only in relation to the other terms following it in the series, and a power such as that of an increment, like the series itself, is here out of place; instead, the simple expression: derived function of a power, or as was said above: function of potentiation of a magnitude, would be preferable — the knowledge of the way in which the derivation is taken to be a development included within a power being presupposed.
§ 622
Now if the strictly mathematical beginning in this part of analysis is nothing more than the finding of the function determined by the expansion of the power, the further question is what is to be done with the relation so obtained, where has it an application and use, or indeed, for what purpose are such functions sought. It is the finding of relations in a concrete subject matter which can be reduced to such a function that has given the differential calculus its great interest.
§ 623
But as regards the applicableness of the relation, we need not wait for conclusions to be drawn from particular applications themselves, the answer follows directly and automatically from the nature of the matter which we have shown to consist in the form possessed by the moments of powers: namely, the expansion of the powers, which yields the functions of their potentiation, contains (ignoring any more precise determination) in the first place, simply the reduction of the magnitude to the next lower power. This operation is therefore applicable in the case of those objects in which there is also present such a difference of power determinations. Now if we reflect on the specific nature of space, we find that it contains the three dimensions which, in order to distinguish them from the abstract differences of height, length and breadth, we can call concrete — namely, line, surface and total space; and when they are taken in their simplest forms and with reference to self-determination and consequently to analytical dimensions, we have the straight line, plane surface and surface taken as a square, and the cube. The straight line has an empirical quantum, but with the plane there enters the qualitative element, the determination of power; further modifications, e.g. the fact that this also happens in the case of plane curves, we need not consider, for we are concerned primarily with the distinction in general. With this there arises, too, the need to pass from a higher power to a lower, and vice versa, when, for example, linear determinations are to be derived from given equations of the plane, or vice versa. Further, the motion in which we have to consider the quantitative relation of the space traversed to the time elapsed, manifests itself in the different determinations of a motion which is simply uniform, or uniformly accelerated, or alternately uniformly accelerated and uniformly retarded, and thus a self-returning motion; since these different kinds of motion are expressed in accordance with the quantitative relation of their moments, of space and time, their equations contain different determinations of powers, and when it is necessary to determine one kind of motion, or a spatial magnitude to which one kind of motion is linked, from another kind of motion, the operation also involves the passage from one power-function to another, either higher or lower. These two examples may suffice for the purpose for which they are cited.
§ 624
The appearance of arbitrariness presented by the differential calculus in its applications would be clarified simply by an awareness of the nature of the spheres in which its application is permissible and of the peculiar need for and condition of this application. But now the further point of interest within these spheres themselves is to know between what parts of the subject matter of the mathematical problem such a relation occurs as is posited peculiarly by the differential calculus. First, it must be observed that there are two kinds of relation. The operation of depotentiating an equation considered according to the derivative functions of its variables, yields a result which, in itself, is no longer truly an equation but a relation; this relation is the subject matter of the differential calculus proper. This also gives us, secondly, the relation of the higher power form (the original equation) itself to the lower (the derivative). This second relation we must ignore for the time being; it will prove to be the special subject matter of the integral calculus.
§ 625
Let us start by considering the first relation; for the determination of its moment (to be taken from the application, in which lies the interest of the operation) we shall take the simplest example from curves determined by an equation of the second degree. As we know, the relation of the co-ordinates is given directly by the equation in a power form. From the fundamental determination follow the determinations of the other straight lines connected with the co-ordinates, tangent, subtangent, normal, and so on.
§ 626
But the equations between these lines and the co-ordinate are linear equations; the wholes with respect to which these lines are determined as parts, are right-angled triangles formed by straight lines. The transition from the original equation which contains the power form, to said linear equations, involves now the above-mentioned transition from the original function (which is an equation), to the derived function (which is a relation, a relation, that is, between certain lines contained in the curve). The problem consists in finding the connection between the relation of these lines and the equation of the curve.
§ 627
It is not without interest, as regards the historical element, to remark this much, that the first discoverers could only record their findings in a wholly empirical manner without being able to account for the operation, which remained a completely external affair. It will be sufficient here to refer to Barrow, to him who was Newton's teacher. In his lect. Opt. et Geom.,in which he treats problems of higher geometry according to the method of indivisibles, a method which, to begin with, is distinct from the characteristic feature of the differential calculus, he also puts on record' his procedure for determining tangents — 'because his friends urged him to do so'. To form a proper idea of how this procedure is formulated simply as an external rule, in the same style as the 'rule of three', or better still the so-called 'test by casting out nines', one must read Barrow's own exposition. He draws the tiny lines afterwards known as the increments in the characteristic triangle of a curve and then gives the instruction, in the form of a mere rule, to reject as superfluous the terms which, as a result of the expansion of the equations, appear as powers of the said increments or as products (etenim isti termini nihilum valebunt); similarly, the terms which contain only magnitudes to be found in the original equation are to be rejected (the subsequent subtraction of the original equation from that formed with the increments); and finally, for the increments of the ordinate and abscissa, the ordinate itself and the subtangent respectively are to be substituted. The procedure, if one may say so, can hardly be set forth in a more schoolmaster-like manner; the latter substitution is the assumption of the proportionality of the increments of the ordinate and the abscissa with the ordinate and the subtangent, an assumption on which is based the determination of the tangent in the ordinary differential method; in Barrow's rule this assumption appears in all its naive nakedness. A simple way of determining the subtangent was found; the artifices of Roberval and Fermat have a similar character. The method for finding maximal and minimal values from which Fermat started rests on the same basis and the same procedure. It was a mathematical craze of those times to find so-called methods, i.e. rules of that kind and to make a secret of them — which was not only easy, but in one respect even necessary, for the same reason that it was easy — namely, because the inventors had found only an empirical, external rule, not a method, i.e. nothing derived from established principles. Leibniz accepted such so-called methods from his contemporaries and so did Newton who got them directly from his teacher; by generalising their form and applicableness they opened up new paths for the sciences, but at the same time they also felt the need to wrest free the procedure from the shape of merely external rules and to try to procure for it the necessary justification.
§ 628
If we analyse the method more closely, we find the genuine procedure to be as follows. Firstly the power forms (of the variables of course) contained in the equation are reduced to their first functions. But the value of the terms of the equation is thereby altered; there is now no longer an equation, but instead only a relation between the first function of the one variable and the first function of the other. Instead of px = y2 we have p : 2y, or instead of 2ax - x2 = y2, we have a - x :y, the relation which later came to be designated dy/dx. Now the equation represents a curve; but this relation, which is completely dependent on it and derived from it (above, according to a mere rule), is, on the contrary, a linear relation with which certain lines are in proportion: p : 2y or a - x : y are themselves relations of straight line of the curve, of the co-ordinates and parameters. But with all this, nothing is as yet known. The interest centres on finding that the derived relation applies to other lines connected with the curve, on finding the equality of two relations. And so there is, secondly, the question, which are the straight lines determined by the nature of the curve, standing in such a relation? But this is just what was already known: namely, that the relation so obtained is the relation of the ordinate to the subtangent. This the ancients had found in an ingenious geometrical manner; what the moderns have discovered is the empirical procedure of so preparing the equation of the curve that it yields that first relation of which it was already known that it is equal to a relation containing the line (here the subtangent) which is to be determined. Now on the one hand, this preparation of the equation — the differentiation — has been methodically conceived and executed; but on the other hand the imaginary increments of the co-ordinates and an imaginary characteristic triangle formed by them and by an equally imaginary increment of the tangent, have been invented in order that the proportionality of the ratio found by lowering the degree of the equation to the ratio formed by the ordinate and subtangent, may be represented, not as something only empirically accepted as an already familiar fact, but as something demonstrated. However, in the said form of rules, the already familiar fact reveals itself absolutely and unmistakably as the sole occasion and respective justification of the assumption of the characteristic triangle and the said proportionality.
From:
Hegel text images from:
Hegel. Wissenschaft der Logik. Berlin: Dunker und Humblot, 1841.
Oresme images from:
Babb, Jeff. “Mathematical Concepts and Proofs from Nicole Oresme.” Presented at The Seventh International History, Philosophy and Science Teaching Conference.

























































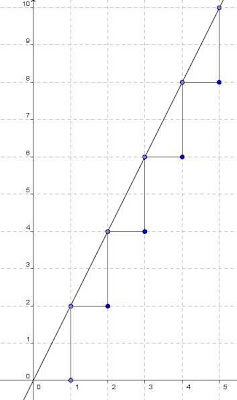
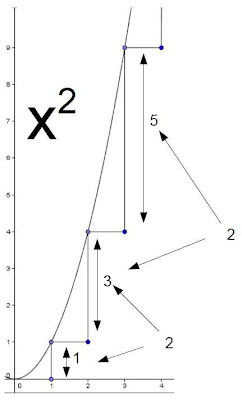















Hi!
ReplyDeleteI thank you very much for this posting. A bold explanation of Hegel and Deleuze! You remind me of Juliette Simont...
Would you please indicate me some introductory book about this subject? The best book I know is MATHEMATICS FOR THE MILLION, by Lancelot Hogben. But maybe there is some other nice book about it.
All best,
Tancredo Braga - tanbra@gmail.com
Tancredo Braga,
ReplyDeleteI tried emailing. Let me know if you did not get it.
Corry Shores
Hi!
ReplyDeleteI've got it.
Carl Boyer, The History of the Calculus and its Conceptual Developments, seems to be the book that covers the subject. But I'm not sure.
I remember reading Desanti, about Hegel and mathematics in the Logic, but it was too technical for me.
I thought that after reading Marx's The Capital, reading Hegel would just be a matter of turning the upside down...kkkk
All best,
Tancredo Braga