The Quantitative Intensity of Oresme's Difformly Difformed Qualities

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Mathematics, Calculus, Geometry, Entry Directory]

Oresme makes the classical distinction between the continuity of measurable things we sense, and the discrete determinateness of conceptualized numbers; hence points, lines, and surfaces – or their properties – must be imagined and represented. Indivisible points and lines are non-existent, but we need to imagine them in order to measure and compare things in the world (Oresme 244B.a).

In the 14^th Century, there was not yet a precise definition of an instantaneous rate of change, although steps to develop one were prepared in the notion of the latitude of forms, that is, of variability of qualities (Boyer The History of the Calculus 73a).

The word 'form' here means: “any quality which admits of variation and which involves the intuitive idea of intensity – that is, to such notions as velocity, acceleration, density” (73b). These qualities are then expressed quantitatively by means of latitude[1] (also termed ‘altitude’). “The latitude of a form was the degree to which the latter possessed a certain quality, and the discussion centered about the intensio and the remissio of the form, or the alterations by which this quality is acquired or lost” (73bc).

They considered many types of change-rates, including distance and intensity of light, heat, and density (73).

We currently represent such rates of change using coordinates along x and y axes. We may treat the x-axis as the longitudinal dimension, and the y as the latitudinal one (Turetzky 10-11).

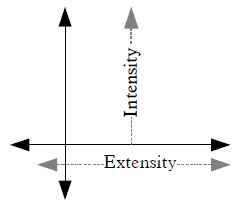
Oresme writes: “every intensity which can be acquired successively ought to be imagined by a straight line perpendicularly erected on some point of the space or subject of the intensible thing, e.g., a quality.” An intensity, “according to which something is said to be ‘more such and such,’ as ‘more white’ or ‘more swift,’” is “infinitely divisible in the manner of a continuum in only one way” and is thus best represented by a line. What is important is that the ratios are maintained between the real thing and the representation. If at one point in time an object is moving half the speed that it does at another time, the represented line should also be half the distance: “equal intensities are designated by equal lines, a double intensity by a double line, and always in the same way if one proceeds proportionally” (Oresme 244 B.bc; 245A.a). Analogically, just as the y-axis is an orthogonal dimension to the x-axis, there are dimensions of intensive magnitude intersecting the spatio-temporal extensities around us, which we may represent with longitudinal and latitudinal intersections.

Although this fourth intensive dimension does not exist, for Oresme, it has a sort of virtual status. Even though "it does not happen that a fourth dimension exists or is imagined, still a corporeal quality is imagined to have a double corporeity: a true one with respect to the extension of the subject in every dimension and another one that is only imagined from the intensity of this quality taken an infinite number of times and dependent upon the multitude of surfaces of the subject” (Oresme 245-246).

We represent the linear quality in terms of longitude and latitude by "figuring" them.

If there is no alteration in the rate of change across some extension (time in the case of velocity), then there is a uniform rate of change, a latitudo uniformis. The points representing the intensity's uniform movement would stay along the horizontal axis, and thus would be figured by a rectangle[2]:

(Thanks Jeff Babb)

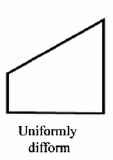
Non-uniform rates of change, latitudo difformis, would be ones such as constant acceleration. Because the magnitude of intensity increases, we would figure it with a triangle or sloping straight line (Oresme 247B.c):

(Thanks Jeff Babb)

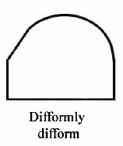
All other forms are ones whose non-uniform rate of change itself is not uniform. These are latitudo difformiter difformis, as for example an irregularly-paced rate of acceleration, which is always the case in the physical world. Oresme says of the difformly difform quality that “it can be described negatively as a quality which is not equally intense in all parts of the subject nor in which, when any three points of it are taken, the ratio of the excess of the first over the second to the excess of the second over the third is equal to the ratio of their distances.” Hence, if the latitudinal line is not smoothly straight, then it is difformly difformed. Latitudo difformiter difformis is “imaginable by means of figures otherwise disposed according to manifold variation (Oresme 248A.a; B.d):”

(Thanks Jeff Babb)

[Site Topic Directory]

[1] latitude, OED: I. Breadth, width. 1. a. Transverse dimension; extent as measured from side to side; breadth, width of a surface, as opposed to length; b. The range within which anything may vary.

[2] Images from Babb, Jeff. “Mathematical Concepts and Proofs from Nicole Oresme.” Presented at The Seventh International History, Philosophy and Science Teaching Conference. Winnipeg, MB, Canada August 1, 2003)

Oresme. “The Configuration of Qualities and Motions, Including a Geometrical Proof of the Mean Speed Theorem” in A Source Book in Medieval Science. Ed Edward Grant. Harvard University Press, 1974.

Philip Turetzky. “Pictorial Depth: Intensity and Aesthetic Surface” Axiomathes (2005) 15: 1–28.