[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Mathematics, Calculus, Geometry, Entry Directory]
[Calculus Entry Directory]
The derivative's geometrical interpretation seeks a curve's tangent line. We may consider the tangent in physical terms as the direction the curve is headed. This direction is the outcome of competing forces. For example, imagine yourself swinging-around a ball on a string in a circle above you. Forces are pushing-and-pulling it in many directions, each with a different quantity, and the outcome of these forces is continual circular motion [1].
If we were to cut the string, we would subtract a force and cause the ball to fly-off in the direction it wanted to go at that point, but was unable-to because other forces immediately counter-balanced that motion. If we cut the string, the ball would flee at a 90 degree angle to the string [2]:
Now we need to imagine something moving with inconstant forces (thus having difformly difform motion), and so its curve is not perfectly circular [3]:
If we release the ball some point along its irregular path, it will travel the direction it intended that moment, but determining its aim is extraordinarily difficult. However, the technique differentiation empowers us to do so. One possible use for it is determining instantaneous velocity.
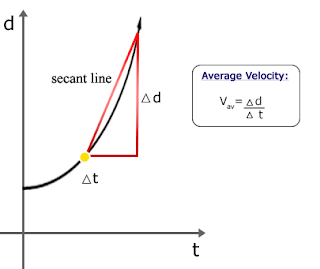
Far simpler is obtaining the average velocity. Consider the y-axis as distance, and the x-axis as time. The change in distance (Δd) over the change in time (Δt), gives us the average velocity in terms of a ratio. That ratio, 2 / 1 for example, can be considered the rise-over-the-run slope for the hypotenuse to the two lines of change, and we consider this line the secant [4]:
But this only tells us where it was headed over a duration of time. We also want to know, where was it headed at only one point in time? In the case of our velocity function, what is its instantaneous velocity? [5]
We see that the instaneaous velocity aims away-from its destination, just as the tied circling ball does not fly straight-off away, on account of the competing forces drawing it in. Thus just like our ball example, where we thought of the forces' magnitudes pushing-and-pulling the ball in different directions – with one motion being the outcome – we can also think of the x and y coordinate-values as magnitudes of force pushing-and-pulling every point of the curve in different directions.
But it seems impossible to make such a determination at a singular point. Why? Because if we want to know something's direction at a point, this would be at a place where there is no extension: no extension along the y-axis, none along the x-axis. But then, we would not be able to calculate the change in y over the change in x, because there is no change at a point, it is instantaneous. Also, the rise-over-run would be zero divided by zero, which is an undefined value.
However, by considering the point as a limit, we may use the derivation technique to find a virtual instantaneous change. If we consider the rise and run values to be in process of becoming a singular point, we may thereby determine the curve's aim at that point's limit.
So we want to find the tangent line for the graph of a function at some point, with coordinates P = (x0,y0). [6]
Here, x0 is some fixed place on the x-axis.
Because this is a function, point P can be obtained by means of the function on x0 to yield y0, which completes the coordinates, hence:
P = (x0,(fx0))
The slope then, m, will be the derivative of f:
m = f’(x0).
Definition: f’(x0), the derivative of f at x0 is the slope of the tangent line to y = f(x) at point P.
Below we see that a point Q was chosen at a distance of Δx from x0. Like we saw in the diagram for average velocity, this is the secant line [7].
The tangent line is equal to the limit of secant lines PQ as Q tends to P; (and P is fixed, while Q is varied).
P is aligned with point x0 on the x-axis:
Then we travel a horizontal distance, denoted by Δx, “delta x”, or the “change in x” [9].
The other component we need is the vertical distance. Because we find y by means of the function on x, we consider this height as Δf [10].
The slope of the secant, then, is Δf / Δx.
But we are looking for the limit, so our slope then is found at the limit as Δx goes to zero [11]:
More clearly, then, the slope of the tangent is [12]:
To obtain a more usable formulation, we will write the Δf more explicitly.
Point P is (x0, f(x0))
[because the y coordinate is obtained by a function on x.]
Point Q is Δx away from point P, hence point Q aligns with x0 + Δx on the x-axis [13]:
Point Q is right up above x0 + Δx, and because we obtain the y coordinates by means of a function, the y coordinate for point Q is f(x0 + Δx). Hence together with the x coordinate, Q’s coordinates are (x0 + Δx, f(x0 + Δx)) [14].
We may write a different formula for the derivative at x0, which is the slope, notated f’(x0). Because it is a slope, it will be a rise-over-the-run, or Δy / Δx, but because the y coordinate is obtained by means of the function, the slope we seek is Δf / Δx. To obtain the rise-over-the-run, that is, the change in f over the change in x, we would need to subtract the right-most values from the left-most along each axis, that is, to use the slope formula:
m = (y2 – y1) / (x2 – x1)
or in our case,
m = (f2 – f1) / (x2 – x1)
By plugging into the formulas above for each value, we have (f(x0 + Δx) – f(x0)) / Δx [15].
This is called the difference quotient, because there is a difference in the numerator, and "in disguise," the denominator is a difference between right and left sides (x2 - x1).
Thus altogether [16]:
We then consider a first example:
f(x) = 1 / x
This function is graphed as [17]:
The doted line is the tangent we seek. But we will find its slope algebraically. To do so, we need to find Δf / Δx. The formula for Δf was (f(x0 + Δx) – f(x0)). When we plug in our function, we (multiplicatively) invert the x values, that is, put a one over them, hence we obtain [18]:
When we remove the embedded fractions (by dropping the top couched-denominators to the entire bottom denominator), we get:
Then we factor out 1 / Δx, to get:
We then find the common denominator by multiplying each denominator by the other denominator to obtain:
This simplifies to:
Then simplified further:
We then distribute the negative in the right numerator to make x0 – x0 –Δx, leaving –Δx, hence [19]:
Then, the Δx on the outside denominator cancels with the enclosed numerator [20].
The last step is to take the limit, as delta tends to zero, and substitute zero for Δx. We can do this now, because before the numerator and denominator gave us number divided by zero, which is undefined. But through algebraic operations, we were able to make the Δx negate-out of the equation without leaving a zero in the denomenator. Thus we now substitute-in the limit, that is, make Δx equal zero, leaving us with [21]:
In total [22]:
Thus [23]:
We then compare with our chart. This is negative, and likewise the slope is negative. Also, as xo goes to infinity, so as x moves to the right, it becomes less steep [24].
[1] Image from http://www.hometrainingtools.com/articles/amusement-park-physics.html
[2] Image from http://www.nightanddaydance.com/journal/
[3], [4], [5] Images from http://www.coolschool.ca/lor/CALC12/unit2/U02L01.html
[6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [17], [18], [19], [20], [21], [22], [23], [24] From MIT OpenCourseWare. Creative Commons Licence. All blackboard images from Prof. David Jerison's 18.01 Single Variable Calculus, Video Lecture 1. Other listed images from Lecture Notes.













































































No comments:
Post a Comment