[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Posthumanism, Entry Directory]
[Bostrom & Sandberg's "Roadmap", Entry Directory]
[My more developed Deleuzean critique of mental uploading can be found here. The following summarizes Nick Bostrom's & Anders Sandberg's new study on whole brain emulation. My commentary is in brackets.]
Nick Bostrom & Anders Sandberg
"Whole Brain Emulation: A Roadmap"
Part III: Issues
Section II: "Complications and Exotica"
[Bostrom & Sandberg detail a plan paving the way for the computer-emulation of human brain activity. Here they address a variety of possible objections to their approach. I have selected three which I think are the most relevant for a Deleuzean critique.]
Subsection 7: "Neurogenesis and Remodelling"
For a long while, many brain scientists thought that our bodies stop generating brain cells in adulthood. Fairly recently, scientists have learned that actually adults still produce new brain cells, although it takes longer than a week at least for the cells to generate.
If we want an accurate emulation of the brain, we will also have to simulate this growth. However, that adds complexities that could severely stall the development of the simulation technology.
Bostrom & Sandberg note that if it takes longer than a week to generate a brain cell, then we do not need to adjust emulations that run for shorter periods of time.
But for the more sophisticated emulations, it will be necessary to model the ways that brain cells grow new connections. This will involve a great deal of research. As well, running neurogenesis simulations will require a large amount of the computer's attention. However, the computer will devote far less of its activity to cell genesis than it will devote to simulating all the other neural activities.
[Bostrom & Sandberg realize that neurogenesis is a problem for brain emulation. Yet, they think it is an obstacle only for research endeavors and for the computer's capacities to compute information. I think they are missing a far more profound complication: the non-computability of creativity.
We notice that one important aspect of neurogenesis is the creation of new connections between brain cells. Two cells that were previously unconnected can become linked through the genesis of connecting cells. Bostrom & Sandberg regard the normal function of the brain as constituting consciousness and intelligence. This creation of new connections is a small addition to the way we think.
But we ask, when are we in a more profound state of thought:
1) when we are performing habitual actions in which we recognize everything in our consciousness, or
2) when we are faced with things we do not recognize, when we have a problem to solve, and powerful forces compel us to make new conceptual connections.
I attest that I am in the most profound states of thought when I take a difficult exam that forces me to invent new concepts and interpretations, or when deadlines force me to write-up original ideas. Certainly the cow is "computing information" by means of brain activity when it recognizes that the grass below him is good to eat. However, we would not expect the cow's brain to make new connections in these instances. Rather, it is when the brain cannot compute information that it truly begins to think, when it makes new conceptual connections. Bostrom & Sandberg presuppose that all mental phenemena have a physical basis. So when we make new conceptual connections, we very likely could be generating new neural connections as well. But Bostrom & Sandberg have a way of dealing with these sorts of problems. They consider these cases to involve informational "noise" or random variables, which could be simulated computationally. We discuss this further in the section on determinism below.]
Subsection 12: "Analog Computation"
[Bostrom's & Sandberg's emulation is based largely on digital computation. (For an extensive examination of the differences between analog and digital, see this entry.)
In our decimal system, we have nine digits. When we add one to nine, we carry to the next place. In any of these places, we might have any of 10 variations, zero through nine. A binary digital system would have only two variations, one or zero. Zero means zero. One means one. But when we add one to one, we do not get 2. For, 2 is not one of our possible variations. Just as when we carried the one when adding it to nine in the decimal system, we likewise in the binary system carry the one when we add it to one. So the decimal value 2 appears as "10" in the binary system. What is important in digital systems is that there are no in-between values. It's either a one or a zero.
Consider instead the doctor's scale that measure's your weight. If it has the sliding weights, then you will see that although there are lines marking determinate numerical values, the nurse might also find the point of balance between markings. This sort of system is analog. Rather than having discrete variables, it has continuous variations. In a sense, analog has the highest potential for precision, because it is not limited to a finite number of possibilities. As a continuum, its scale can be divided infinitely (in theory), and so there are an infinity of variations possible.
This presents two complications for brain emulation
Problem 1:
Consider the abacus. Either the bead is on one side, or it is not. We do not read the beads like the doctor's scale, where the distance on the bar changes the value. The abacus reads either one value, or it does not. And it does not give any values in between its designated digits. So the abacus is in either a state reading one value, or it is in a state reading another value, with no in-between possibilities. Hence the abacus has "discrete states." Likewise, digital computers are also discrete-state machines. So they have a finite number of variations, even if they can process many of these limited variations in a short amount of time.
Brain cells transport electrical "signals." According to one view, these signals are transmitted as discrete states: either the signal is transferred, or it is not transferred. However, according to other brain researchers, at least some cases of signal transfer are matters of more-or-less. And these quantities of electrical signal being transferred fall along a continuum of possible variations. In other words, at least some of our brain's "information processing" might involve analog computation.
The problem then with Bostrom & Sander's plan is that it relies primarily on digital computation, which is always limited to a finite range of variations. But if our brains are analog, then the digital simulations will never be able to process as much information as our brains do.
Problem 2:
We know that it is possible that our brains may process nervous signals analogically. But consider when we increasingly turn-up a light using a dimmer switch. We do not first sense the light as being in one state, then later in another state, with no variations in-between. Rather, we perceive an unbroken continuum of increase. The world around us does not seem to be made up of so many clearly distinct things. Rather, many theorize that our senses send our brains continuously varying signals, and our minds draw their own distinctions that define differences, according to the given situation. So even if our brains process information digitally, they still receive it analogically. Another problem is that we also store this sense-data in its analogical form. Because for example we might see a sunset and note that the sun completely set during some 15 minute period. But later we might need to specify more closely when it set. Then we go back into our memories and narrow it down to a five minute period. So even if the brain emulation was equipped with analog sensors whose signals are processed by an analog-to-digital converter, we will still have to deal with the problem of storing analogical data, which would be difficult if its data storage uses digital circuitry.
Also, we want to create an emulation that is no different from human consciousness, even in terms of subjective experiences or "qualia." But if the emulation is digital and it only computes digital data, then it will not be able to have subjective experiences of the continuity of the world around us. Hence digital "phenomena" might be qualitatively different from human phenomena. If this is so, digital simulations will not accurately emulate human consciousness.]
Bostrom & Sandberg offer two responses to the objection that there is a qualitative difference between the continuous variables of analog and the discrete variables of digital.
Response 1: Reality is fundamentally made-up of discrete quantities (or quanta).
If brains compute analogically, then they may "make use of the full power of continuous variables" (38). Because then the brain would be computing an infinite range of variations, it would be able to compute on a hyperbolic level; it would be capable of "hypercomputation." This would allow it to calculate things that digital computers could never conceivably compute, because digital computers are always limited to a finite range of variations processed in a finite amount of time.
However, our brains are made-up of discrete atoms. Quantum mechanics has determined that atoms take on only discrete energy states. As well, some findings of quantum physics suggest that space-time is not a continuum but rather is made-up of discrete units.
If time-space is made up of discrete units, then the world around us is fundamentally digital to begin-with. According to this view, we are mistaken to think that there are ever any continuous nerve signals. For, energy states are fundamentally discrete units (quanta), and they travel through discrete time-space units as well. Hence there is really a finite range of variations that the brain would need to process. Thus it would be conceivable that a very powerful and sophisticated computer could process all possible signals in a finite amount of time.
[Here we see that Bostrom & Sandberg construe analogical computation as hypercomputation. That is to say, analog is the same as digital taken to an extraordinarily high level. In other words, they see analog not as qualitatively different from digital, but really as quantitatively different.
Their solution is to argue that reality is fundamentally digital or discrete. Therefore, there is no qualitative difference between what we think are continuous changes and their digital simulations. For in reality, both are digital at the fundamental level.
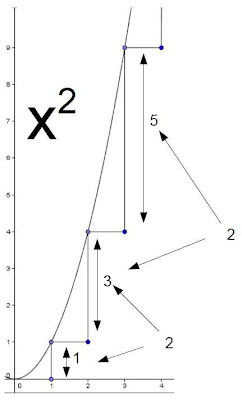
To present our Deleuzean critique, we imagine ourselves jumping out the window. We know that gravity causes us to accelerate at a constant rate. To make things easy, we will imagine that for one reason or another our rate of acceleration is x-squared. So we can easily determine how fast we are going at any time point. We merely square the value of the fall-duration. So after one second, we fell one meter. After two seconds, we fell four meters. After three seconds, nine meters, and so on. Let's also suppose that time is made up of discrete units. To make our chart simpler, we will place a dot at every quarter unit of time. It is important for this demonstration that we perceive graphically the discretion of time, so we pretend that really we are looking on a very small scale of time-change.
So to each discrete time-point corresponds a discrete distance-point. Below we see the pattern of distribution of these discrete correlates.
We see that as time goes on, the differences of distance-traveled between time-points increase at a steady rate of change.
Still there is a temporal succession. Each instance proceeds to the next. So at any given moment, the change is tending towards another value. Let's look below at the first tendency of change. We use a line to depict the direction that the first correlate is tending, which is determined by where it ends-up the next instant.
Now let's examine the next tendency at the next discrete time point.
Then the next.
We see that the tendencies get stronger. The steeper they are, the larger the change in distance from time-point to time-point. Let's follow the next set of changes.
We see that there is a pattern to the changes.
The changes seem to increase continuously. We see that the differences between each point are not the same, but if we look at the differences between the differences, we see that they are the same.
We will chart out a series of values for x-squared.
Then we see the differences between the x-squared values.
We note that they are different. Each time the difference gets larger. But if we look at the differences between those differences (which would be the changes of the changes between discrete time points),
we discover that the change of the change is continuously the same. [see the entry on Hegel's calculus for a more thorough examination of higher order continuities.] So on the level of time and space, there are tendencies that keep changing from point to point. But on a higher order of change, there is a continuity to the change. Gravity accelerates objects at a constant rate. That means that even if time-space is discrete, changing changes are continuous.
Now as we fall from the window, let's presume that the faster we are moving, the more sensation we feel. So at each discrete time point, the nerves are sending a signal of some discrete quantifiable energy-level. Even so, because gravity accelerates our speed, the rate of those discrete sensation-changes is in continuous variation. Even though this continuous variation manifests as a discrete value at each time point, the change of the change virtually continues its change between time points. For, we know that the rate of change is continuous, so it must continue its change between temporal points. We can say that if hypothetically there were another time-point between two other time-points, we can predict what distance correlates with that virtual or hypothetical time-point, because we know the continuous variation of change. In other words, there is a virtual continuum even if there is not an actual one.
If we imagine a sound whose volume increases slowly and steadily, eventually we come not to notice the change so much. For, it becomes predictable. But if the volume-increase accelerates, then we might pay more attention, because it becomes more difficult to predict. In other words, what made the sensation of the accelerating sound a greater sensation was not that it was at a higher volume. Rather it was a greater sensation because the change of its changing was greater. And if the accelerations changed in an unpredictable way, then this would be a very intense sensation, from a Deleuzean perspective.
So we see that a Deleuzean critique would say that there is a form of analog on a higher order, even if on the most fundamental lowest level there is nothing but discrete units. So a simulation of human sensation would need somehow to deal with values that vary continuously in an analog way. Thus Bostrom & Sandberg cannot emulate human consciousness using only digital systems. In fact, they recognize that if whole brain emulation continues to fail, it could very well be on account of the inability of digital computers to compute continuously varying values.]
Response 2: Analog is somewhat imprecise, and digital can be made less imprecise than analog.
Bostrom & Sandberg consider for the sake of argument that all our brain's functioning is analog. Now imagine for example an analog audio recording-device that is somehow capable of making a perfect imprint of the continuous variations of the sound-signals it is recording. Even so, there are other factors that interfere with the fidelity. For example, electrical disturbances from various sources external and internal to the recording device will add a small amount of "noise" or distortion to the signal. This same phenomenon happens to our brain signals. So even if the signal is continuous, there is still a ratio of good signal to unwanted interfering signals, called the "signal-to-noise ratio." In other words, even if the brain were an analog processing system, it would still have a margin of error or imprecision.
Bostrom & Sandberg then argue that
1) this margin of imprecision has a discrete finite value,
2) we can increase the number of variables that the digital computer can compute by increasing its speed.
Thus, we may keep increasing the computer's speed until it is just as imprecise as the analog signal. So even though digital signals inevitably miss intermediate variables, this will not matter. For, the amount of variation that digital misses will be no less than the amount of variation that analog gets wrong.
[Here again we see Bostrom & Sandberg presuppose that there is only a quantitative difference between analog and digital. For, they assume that the main difference between an analog signal and a digital one is the amount of variables they may compute. However, consider this scenario. We bypass someone's normal vision signals with digital ones that miss no more variables then the normal analog vision-signal gets wrong. The person might be able to make-out everything in her field of vision just as well. But that person might still say that her experience of seeing feels different. In other words, there can be a qualitative difference between precise digital and analog sensation signals. As an informal demonstration, I invite the reader to listen to an Aerosmith album from the 1970's on vinyl record. Then, listen to it on the more advanced digital format, superaudio (or dvd audio). The digital is incredibly precise. The instruments in fact sound pristinely clear. But the music feels different. Aerosmith music does not seem to feel right when it losses its "muddiness." Anyone who undertakes this demonstration might as well wonder if in fact the more precise the digital, the more qualitatively different the experience. To put it another way, making digital more precise does not make it more analog, rather, making digital more precise makes it more digital, that is, more qualitatively different from analog, even if in a less explicable way.]
Subsection 13: "Determinism"
If nothing is random in the world, then everything theoretically could be predicted, provided that we had enough information. But that would mean that the decisions we make are also predetermined. If there are no unpredictable factors influencing how we think, then programming the software emulating the human mind will not face ultimate complexities. However, if mental events are subject to random variables, or if we have the capacity to make decisions according to a free will that is not reducible to physical pre-determinable factors, then it might be impossible to emulate the human mind.
In fact, Bostrom & Sandberg acknowledge that randomness is important for the development of certain neurological structures. To that end, they suggest we use random-number generators to incorporate "pseudorandom" variations into the simulation.
The generators can be used to incorporate variations for all known variables. However, there is the possibility that there are "hidden variables." Or according to Donald Rumsfeld's epistemological system, there are known-knowns, known-unknowns, and unknown-unknowns. If there are only known-unknowns, then randomness is not a problem. But if there are unknown-unknowns, then there is no way to use computer programming to simulate them.
Bostrom & Sandberg write-off this problem by noting that while hidden variables are
not in any obvious way directly ruled out by current observations, thereis no evidence that they occur or are necessary to explain observed phenomena.
[From our Deleuzean critical perspective, we would note an even deeper problem that this dismissal does not address. They regard the hidden variables as being ones that are there, but which we do not know about. This is also like reducing chaos to hyperbolic complexity. In other words, this regards randomness not as pure chance, but as nearly impossible to statistically calculate. For, there are so many variables, many of which are unknown, that we cannot expect ever to incorporate all of them into our calculations. Their response is that there is no evidence yet that either this is so, or that it is a problem.
But consider this possibility: there are unknown variables, and there are two factors regarding their variation:
1) sometimes these variables are there, and sometimes they are not
2) sometimes these variables vary to one extent, other times to another extent.
So we here are consider the possibility that there are variations in the variations. In other words, that perhaps there are higher-order variations. And perhaps as well each order of variation has an even higher one, and thus there is infinitely varying variation. This would be akin to Deleuze's Nietzschean dice throw: pure chance, pure unpredictability, pure randomness, pure chaos. There is no more evidence to say that chaos is reducible to complexity as to say that chaos cannot be reduced to anything but more chaos. In fact, Bostrom & Sandberg use the lack of counter-evidence to their position as support for their argument. But does not the fact that we cannot prove that there is a fundamental order suggest instead that by default we would assume there is chaos? In other words, it seem that because we do not know for sure that there is order, we should presume that there is chaos, until proven otherwise. For chaos is what we first notice, and have yet to disprove.
Thus, it does not matter whether the computational hardware is analog or digital. Analog can compute continuously varying variables, but it cannot compute infinitely varying variation. In other words, if reality is fundamentally difference in itself, then reality, mental or otherwise, cannot be simulated. It can only be affirmed.]
Sandberg, A. & Bostrom, N. (2008): Whole Brain Emulation: A Roadmap, Technical Report #2008‐3, Future of Humanity Institute, Oxford University
Available online at:
Nick Bostrom's page, with other publications:
No comments:
Post a Comment