by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Posthumanism, Entry Directory]
[Deleuze, Entry Directory]
[Corry Shores' Finished Writings, Entry Directory]
[Some images to be credited. May I thank Artificial Intelligence philosopher Aziz Zambak for donating his AI research, and my father Ebbie V. Shores for his technical expertise. This entry is dedicated to Jeremy Cubas.]
"Do Posthumanists Dream of Pixelated Sheep? Mental Uploading under Deleuzean Critique"
Part 5: "Deleuze's Analog, Digital, Isomorphism, and Aesthetic Analogy"
Analogical and Digital Replication
The more widely known usage for the terms analog and digital is their application in distinguishing two main types of electronic recording and communication technologies. We might already be familiar with the different ways that music sounds on an analog record turntable as compared to a digital compact disc player. By making metaphorical use of these technologies, Deleuze is able to contrast direct material modes of mediation with indirect immaterial ones. To offer more clarity on this distinction, we turn to John Haugeland’s and James Blachowicz’ papers on analogical and digital computation, which serve as well to characterize their modes of replication. In Haugeland’s “Analog and Analog,” he assigns three qualities to this format: smoothness, sensitivity, and dimensionality. Blachowicz suggests the example of vinyl record cutting, so we will briefly explore this illustration.[i]
In his article “Digital Theory,” Allen Mornington-West explains that sounds move through the air as waves of pressure, which vary continuously and fluidly, as we would expect of this gaseous medium.[ii]
When we hear a sound, vibrating air molecules themselves do not move across the room from the instrument to our ear. Rather, waves of compression and rarefaction pass through the medium (air) in longitudinal waves. Consider a spring held taut, and imagine someone gripping its center, pulling it to one end, and letting it go:
A compressed band of coil-density will then spring to the other end – and back again – until its energy expires. The coils’ displacement (their squeezing together as the compression-wave travels through them) moves parallel to the wave’s outward direction. Air molecules act like these spring-coils when sound-waves pass through them. However, for convenience we will represent this wave-action using a transverse-wave depiction: imagine instead that the person holds the spring near one end and pulls downward before releasing it:
A bulge in the spring would then travel outward, rather than a band of compression; hence, the coil-displacement moves perpendicular to the waves outward motion. When depicting waves this way, the vertical axis represents the degree of compression or rarefaction (higher is greater compression); and, the horizontal axis – representing time – serves to indicate the number of compressions-per-second, which is the wave’s frequency. (Below we see the correspondence between the bands of compression on the bottom longitudinal wave and the peaks of the top transverse wave).
The air waves encounter a microphone’s diaphragm, which causes it to oscillate back-and-forth in concord with the air-waves’ pressure-changes.
The diaphragm is attached to a coil of wires, which then moves in-and-out overtop a fixed magnet. This interaction causes the electrical current to shift to-and-fro through the wires extending from their coiled-formation around the magnet. The current, then, oscillates forward-and-backward at the same frequency as the air-waves, and moves with a proportional amount of force (the voltage). The current emanating from the microphone is the electrical sound ‘signal,’ which in this case is analog for two reasons: 1) the variations of amplitude and frequency change continuously; and 2) the movement of the electricity is an ‘analog’ (an analogy) of the air-waves; for, it mimics their movement in another medium.[iii] If the signal were amplified adequately enough to power a speaker – which is structurally equivalent to a microphone, although with a larger magnet and diaphragm – the back-and-forth oscillation of the amplified current would move the speaker-diaphragm in-and-out in concord with the microphone’s mechanisms, thereby replicating the original sounds. Public address systems operate this way.
If we wanted to record the current-patterns so that they could be replayed numerous more times, one option is vinyl-record production, which involves a blade first cutting a spiral grove into a circular mold, and then using that mold to produce countless replications in plastic. (Below we see the record-cutting blade):
While scoring the mold-material, the blade-mechanism modulates its movement up-and-down in accordance with the sound-signal’s frequency and left-and-right in proportion with shifts in voltage (whose variations parallel those of the original sound-wave’s amplitude).
(The left image looks down upon a track resulting from no sound and hence producing no variation; the middle one displays the back-and-forth cutting movement; and, the right one is the up-and-down motion, creating a deeper or shallower groove). After the album is pressed from the mold, it bears a spiral-form of grooves:
The turntable needle then glides along the track, analogously to the blade’s cutting motions, thereby reproducing the variations in frequency and amplitude. (In the image below, the left track shows the movement of the cutting blade, the right one displays the turn-table’s play-back needle moving analogously):[iv]
This example illustrates Haugelands’s description of analog. We see that the variations both in the air-movement and in the record-cutting are continuous and unbroken (gapless); this is the smoothness of analog. The slightest alteration in the blade’s movement changes the groove’s structure, which will be heard in playback; hence analog has sensitivity. Also, in record-cutting there are two main dimensions of variation in the mimicries of the sound movements: frequency and amplitude. It did not matter how those dimensions manifested, (whether as the movements of a diaphragm, the oscillations of electrical current, the subtle shifts of a record-cutter, the structural features of the groove it carves, or the play-back needle’s sensitive tracings along this delicate imprint). It was only important that the two dimensions were preserved proportionally (analogously) throughout their various manifestations, which is analog’s dimensionality.[v]
The feature of analog that Deleuze most emphasizes is this continuous modulation (variance) of a medium’s dimensions. To better illustrate, we might consider the amplitude modulation of radio waves (AM radio). Through this process, an original sound signal is communicated by modulating (varying) the amplitude of a much higher-frequency radio-wave. Because this radio carrier-wave is so much ‘denser’ than the original sound-signal, when we modulate its amplitude at-pace with the sound-wave, it behaves as though it were a ‘material’ that we carve so it bears (carries) the lower-frequency sound-signal.
(The dense modulated radio-wave is broadcast through the air so our AM radios may demodulate it back-into the original signal, just as our turn-table needles ‘extract’ the signal by sensitively detecting modulations in the record-groove). Thus, we see that in analogical replication, certain dimensions of one medium are modulated to serve as imprints bearing the variations of another medium, thereby transmuting the original form’s embodiment without transforming these formal variations.
However, in digital we both transform and transmute the medium. If for example we wanted to convert the analog sound-signal to a digital one, we might use a digital-to-analog conversion circuit (called a ‘flash converter’). Of course, we will not detail its workings. Instead, we will identify two of its operations that are relevant to our philosophical interests: reductive homogenization and codification.
1) Reductive homogenization. Such a conversion-device receives a continuously-varying analog wave-form as its input, and takes a sample (or a ‘picture’ if you will) of the wave-form at regular periods of time, ignoring the variations in-between. This reduces what was previously a rich fluid wave into a series of magnitude-values (which are the quantities of the oscillating electrical-signal’s voltage that are analogous to the peaks and troughs of their respective air-born sound-waves). Hence, the heterogeneities of the flowing analog wave become a staircase-like reduction. (In the two diagrams below, we see the original wave ‘sampled’ at regular temporal intervals).
2) Codification. By channeling the electrical signals through a series of ‘logic gates,’ the information is reduced to sequences of on-or-off (signal or no signal) patterns that later can be decoded by a digital-to-analog converter, which produces the same staircase-like wave that was previously coded. (In the diagram above, we see that at regular intervals the conversion device assigns a unique sequence of ones and zeros, thereby coding the wave-form).
Thus in a way, digital encoding deletes much of the wave-movement in-between the sampled points.[vi] However, if the gaps are small enough, then when we hear them, they will ‘blur’ together, as Steinhart claims, so to simulate the original analog form.[vii] This code can be rendered and stored in numerous formats, one being the compact disc. In this case, the on/off patterns of the digital code are rendered as pits in a surface of a disc that is read by a laser.[viii]
To illustrate homogenization and deletion another way, we might consider how digital images are composed of smaller squares. (In the left “Pixelation” column
we see how at base digital images are composed of minute ‘pixels’ with perfectly homogeneous contents. The right “Compression” column depicts how a digital image can progressively be rendered more homogeneous. By viewing these reductions, we might imagine how in the first act of digital coding, the original thing’s heterogeneous features were compressed, as it were, into homogeneities).[ix] We ask: would Moravec’s uploading ‘pixelate’ or ‘sample’ our minds, leaving much of who we are behind?
Once the homogenized sound or image has been converted to a code, it can be replicated endlessly and flawlessly. Haugeland calls this advantage of digital its copyability. Also, despite the vast variety of sounds that we may code, we use no more than two symbols (1 and 0) in each case, although within the coded sequence there may be an enormous succession of just these two numbers. The need for these extensive sequences is what Haugeland considers digital’s complexty. Also, it does not matter whether or not the code is stored on a computer chip, compact disc, or even written down on paper. So long as there is some decoding device, then given any possible medium, the fidelity will be the same, and this is the medium independence of digital.[x]
We explore these technical examples, because they illustrate the features of digital which would allow our minds to be copied and transferred to computers. Yet, if our brains’ operations involve analogical processes, then mental uploading will not succeed; for, digital processing would delete much of our mental workings when reducing it to code, and thereby deplete most of who we are and how we think.
Analogical and Digital Computation
We will explore now the analog/digital distinction in computational theory, on account of its rich and well-developed debate spanning much of recent history, and also because computation is immediately relevant to our topic of mental uploading.
We may begin with two examples of simple mechanical computers: the slide-rule and the abacus.[xi] Both perform mathematical computations; yet, what makes the slide-rule analogical and the abacus digital is their different manners of representing numerical values. We compute numerical values on a slide rule by sliding one rule (ruler) past another and then relating their (logarithmic) scales to each other.
(Below we see the top rule C sliding across bottom rule D. We multiply 2 and 3 by lining-up C’s starting-position with the line on D displaying the first number of our equation, the 2. We then look on rule C for the second number of the equation, the 3. Finally, we peer below the 3 to see the answer, 6).
2 x 3 = 6
What is important to note is the continuous sliding of the rules. Any slight movement will change the numerical value, and it will alter according to the magnitude of the movement. Also, the slide-rule’s readings are approximate and open to the viewer’s interpretation.
In contrast, an abacus does not have a continuous scale of values, but rather discrete counting-markers:
For example, to add 1 and 2, we begin with one bead marking the number 1, then move two more beads to obtain 3:
(Of course the more complex functions of the abacus are of practical use). Theoretically, the bead-columns could be assigned any desired decimal place; thus, one can compute any number no matter how minute. Nonetheless, every numerical outcome on the abacus will be a determinate unit, rather than some ambiguous value as is the case with the slide-rule. Thus, we never obtain from the abacus an ambiguous and re-interpretable value.
The abacus is digital and the slide-rule is analog; yet, the precise criteria for distinguishing these types of computation has been a matter of debate. We will merely present here the research most relevant to the topic of neural processes.
As we noted, the abacus’ numerical units are discrete markers, and those of the slide-rule are continuous. When making this distinction, many computational theorists refer to Nelson Goodman’s text, Languages of Art, An Approach to a Theory of Symbols, which provides one of the earliest attempts to differentiate analog and digital. Here he distinguishes density from differentiation, and continuity from discretion. Analogical values are placed along a continuous scale, and between any two values is a third: this is its density, which implies that all readings are approximations, because there can be no pinpoint determination, only more-and-more precise possible readings. Digital uses discrete units, and thus each value is differentiated from the others. Every value-arrangement on the abacus is a discrete state, because there is no ambiguity as to the number it signifies. Each unique and discrete state symbolizes only one possible value that cannot be made any more precise, as would be the case if we took a microscope to the slide-rule so to obtain a more accurate reading.[xii] We might consider another familiar example, digital and analog clocks. A digital clock displays determinate numerical units changing at fixed regular periods; yet, they do not display measurements of the temporal values between these units. Analog clocks, however, show the fluid continuous passage of time, by means of its flowing second, minute, and hour hands.
In terms of computers and their computational operations, James Moor writes that
in a digital computer information is represented by discrete elements and the computer progresses through a series of discrete states. In an analogue computer information is represented by continuous quantities and the computer processes information continuously.[xiii]
This distinction becomes important when trying to describe the functioning of the human brain: do our minds work using discrete units of information or variable values? To better understand the difference, we turn to Fred Dretske’s Knowledge and the Flow of Information. Here he argues that our senses give us an analogical stream of information: they present a changing world whose objects’ properties alter in fluxional continuum. We may watch the setting sun and observe intently as it finally passes below the horizon. Yet, we do not know that the sun has set until we convert the fluid continuum of sense impressions into concepts, which are discrete units of information, and are thus digital.[xiv] While the sun is setting, we may convert our sense data into concepts by sorting them according to the binary distinctions: ‘day’ or ‘night.’ However, while in their act of observation, our senses themselves did not make such precise determinations, but rather experienced a gradual transition. The sun’s continuous movement is dense because we could perform Zeno’s operation and always find a more precise point in time when the sun officially set entirely. Thus for Dretske, the way our brain derives concepts from sense-data resembles analog-to-digital sound-conversion, because it deletes information so to obtain determinate concepts, whose advantage is their ease of processing and transferal (communication).[xv]
Whether brains are digital or analog has relevance not just to artificial intelligence theories, but also to mental uploading, because if the operations of the human brain are not digital, then they cannot be fully replicated on digital computers. In fact, a digital rendition of an analogically-operating mind could not even be functionally isomorphic, which requires that the machine pass from states A to B in-parallel with the brain. However, analogical operations cannot enter into such discrete states. They are never exclusively in a state A, but are rather passing continuously through indeterminate overlapping states. Hence, a digital intelligence could not be functionally isomorphic to an analogical brain.
Hava Siegelmann briefly narrates the history of the debate over the analogical and digital activities of the brain in his article “Neural and Super-Turing Computing.” Siegelmann writes that at a 1943 conference aiming to find the parallels between brains and computers, Warren McCulloch presented the first computational model of the brain neuron, and he portrayed the nervous system as though it were a “finite interconnection of logical devices.”[xvi] He argued that “the activity of the neuron is an all-or-none process;” which is to say, that it is always in a discrete state. It is binary, digital, and functionally similar to logic gates, which receive logical values as input (1 or 0, true or false, on or off), then give a single value as output. Such operations are often found in the workings of digital circuits. (For example, a NOT gate inverts the value of its input, so if it receives a 1, it produces a 0, and vice versa). Below we see a diagram of one of McCulloch’s proposed arrangements of neuron-connections, in this case functioning as inclusive disjunction, (either a or b yet possibly both). [xvii]
A debate ensued, because Gregory Bateson contended that brains also analogically process continuous variables; yet, McCulloch offered a much simpler model that could be applied to known digital computer technology, and hence McCulloch’s theory of neural functioning prevailed for much of the 20th century.[xviii]
However, in the late 1980’s, the analogical model was revived, primarily for two reasons. 1) Neuroscientists demonstrated that in fact neurons operate analogically as well as digitally. In his Consciousness and the Computational Mind, Ray Jackendoff cites research suggesting that the “rate and pattern of firing, which are continuously variable, also can play a role in neural interactions.”[xix] Also, Hubert Dreyfus cites John von Neumann as writing that neural signals “convey meaning by certain analogic traits.”[xx] Thus, if we consider neurons in terms of their being in a ‘firing or non-firing state,’ then we are examining their digital operation, but if we emphasize the ‘ongoing chemical processes’ of the brain, then we are looking at their analogical functioning.[xxi] 2) Human brains learn and adapt to the information they receive, which is not possible with strictly-digital operations. For example, in the case of the sunset, we might later find ourselves in a situation where it is relevant to determine what we were doing just before the sun completely set. To make this assessment, we would need to recall our experience of the event, and readjust our sensitivities for a new determination, or as Dretske writes, “as the needs, purposes, and circumstances of an organism change, it becomes necessary to alter the characteristics of the digital converter so as to exploit more, or different, pieces of information embedded in the sensory structures.”[xxii] On the level of neurons, adaptation and learning occur on account of the information being transferred through ‘chemical gates (synapses)’ that direct the flow through dendrites, which create new connections according to the nature of the overall signal-processing system reacting to the contingencies of each situation. When fresh connections are required for channeling new sorts of information, they are produced all on account of the brain contending with ‘analog physical values’ (analogical sense data) that have many possible ways to process them; and, the neurons must perform ‘continuous time updating’ so that adaptations occur in immediate response to changing contingencies of the environment, which “digital models of computation cannot handle.”[xxiii] Currently, artificial intelligence theorists are developing ways to integrate analogical with digital modes of information-processing in artificial intelligence systems, so to better model human intelligence.
Hence, based on these developments in computational theory, we conclude that mental uploading would fail to fulfill its very own criterion, functional isomorphism. If it is true that our brains’ continuous analogical functioning is indispensable to the way we think, then discrete-state digital simulations cannot replicate our neural activities. However, one may argue that a hybrid analog/digital computer can be invented to remedy this problem. We turn then to Deleuze's aesthetic communication theories to provide a critique for both mental uploading and the proposed hybrid solution.
Analogical and Digital Language
We will first address the research on animal communication that Gregory Bateson discusses in his Steps to an Ecology of Mind, a text that Deleuze cites when distinguishing analog and digital language. According to Bateson, the ‘messages’ that animals convey refer not to objects but to their social relations; for example, the cat’s mewing does not mean milk, but ‘dependence.’ A more compelling illustration is his story of a wolf-pack leader catching an inferior male who broke the code of hierarchies, and achieved coitus with a female, which involves being locked-in with her. Bateson explained previously how an adult wolf weans young puppies by crushing them down with its jaw. Then, in the case of the leader finding his subordinate infringing upon his mating prerogatives, instead of attacking, the leader simply crushed the male down as though weaning him. This communicates their social relationship by analogy: ‘just as a father is to a puppy, I am to you.’[xxiv] In general, most animals normally convey their interrelations by means of such an analogical language, which consists of paralinguistic and kinesic expressions (body language) that communicate magnitudes of social relations (such as being more or less dominant) by means of analogous changes of magnitudes in bodily expression. Deleuze himself defines analogical language as one of relations, which consist of “expressive movements, paralinguistic signs, breaths and screams, and so on.”[xxv]
In analogical communication, the animal (or human) is said to modulate (vary some property of) its physiological expression: it might, for example, increase the tension of its vocal chords, the height of its posture, or the opening of its eyelids. (Below we see a diagram displaying two variables of canine expression: ear height and fang exposure. This image exhibits the continuous variability of modulation: the physiological expression varies more or less, and is not so much a matter of a binary either...or differentiation).[xxvi]
These modulations are felt proportionally in the receiver’s body, and thus their intended meaning is discerned physiologically rather than abstractly: the more a wolf shows his fangs, the more physically intimidated I feel about its power over me.[xxvii]
Contrariwise, in the digital language of human beings, purely arbitrary and conventional signs “have no simple connection (e.g. correspondence of magnitude) with what they stand for.”[xxviii] The symbol for the number 2 need not be double the size of the symbol for 1, in order for it to be twice the numerical value. The symbol 2 is only a name for a magnitude; and these names refer primarily to objects. Bateson illustrates the difference between analogical and digital communication with the example of a man professing his love to a woman, who pays equal attention to the man’s bodily expression as to his words’ meaning, so to find some physically communicated indication of the magnitude of his love for her.[xxix] Deleuze derives from Bateson the following notions which help him explain his philosophy of thought and selfhood. 1) Analog communicates directly through bodily expressions, whose magnitudes of physiological modulation by-pass our faculties of representation and abstraction. Also, because these expressions are not under our rational control, Deleuze will consider them as introducing chaos into thinking. And, 2) digital mediates indirectly through symbolic codes whose physical appearances bear no necessary relation to the information they convey. Also, their meanings are fixed and predetermined, and thus digital supplies the orderliness of thought.
Digital and Analogical Aesthetic Communication
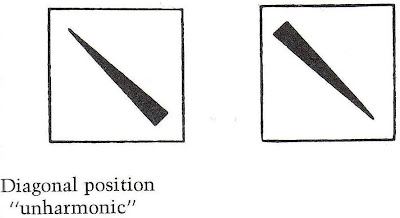
Deleuze characterizes digital and analog as two modes of communication in art. He finds digital coding in abstract art, where figures lose their completeness by eliminating their complexities and condensing them into simple geometrical arrangements, by “reducing all forms to the smallest number of forms of which we are capable of thinking – straight lines, some angles, arcs of the circle and the ellipse.”[xxx] The internal binary relations of these abstract forms allow them to signify by means of symbolic coding. The codes are digital in the metaphorical sense of the fingers as digits that ‘count’ the painting’s formal elements and group them according to formal binary oppositions.[xxxi] Depending on the formalization of the elements, certain effects are produced in the viewer who ‘decodes’ these forms according to their relationships with the other formal elements. For example, painter Wassily Kandinsky reduces a dancer’s posture to a simple linear arrangement; and, the ways these lines are oriented toward each other code a certain effect, in this case un-harmony.[xxxii]
As well, Kandinsky explains how the distributions of tonal ‘weight’ throughout the canvass can be mathematically calculated to determine how they will be decoded by the viewer. Weight is the relative amount of ‘tone value’ or ‘chiaroscuro,’ the amounts of shading between black and white, with more darkness bearing greater weight.[xxxiii]
In this way, Kandinsky tries to eliminate the spontaneous influence and expression of his hand with very controlled strokes that exclude chance and chaos from the painting process. Doing so places precedence on the function of the artist’s eye; he may create much of the painting at a safe distance by using formal observations and manipulations conducted in his mind, thereby subordinating the hand to the eye’s service. The hand becomes reduced to a “finger that presses on an internal optical keyboard” that calculates and controls precisely where the paint will be placed, as though the hand had no autonomy or personality of its own to contribute to the paint-strokes.[xxxiv] On account of this control, the different sections of the blank canvass have unequal probabilities for what may be placed within them, because, for example, if the artist decides to have a certain decoded effect like ‘dramatization,’ then it becomes more likely for images to be placed in the bottom half of the painting (according to Kandinsky’s formula). Thus, the binary coding of abstract art maximizes the cerebral and visual interaction with the painting, and minimizes the sensuous and manual.[xxxv] What results from these techniques are works such as Kandinsky’s Transverse Line:
By contrast, Deleuze finds analogical modulation in action painting, in which the painter expresses a chaotic bodily flux. Techniques of this sort include scrubbing, sweeping, and wiping the wet paint, or throwing paint on the canvas. Here the hand is free to express itself with involuntary movements that create chaos on the canvass rather than controlled forms, which reduces the whole painting to catastrophe.
By letting the thrown paint fall in its own way, and by letting it splatter beyond the edges of the canvass, the action painter almost completely submits the painting’s creation to chance. In Jackson Pollock’s drip paintings, for example, we see the dominant role his hand plays in creating the chaotically arranged splatters on his canvass, which is laid horizontally on the ground and in the middle of a wider distribution of drips.
Here, nearly every part of the canvass has equal probabilities for what may be placed in them, because, as is especially the case with thrown paint that falls outside the borders, no section of the painting is oriented by a center and edge of the canvass.
In these paintings, there are no delimitations, and lines continually and randomly change their directions.[xxxvi] Below is one example, Pollock’s Untitled (Green Silver), 1949. (Color image found on panel beside page 38).
Just as was the case for language and replication, analogical communication functions by means of modulation, which is a continuous variance of some feature. The force Pollock employs to throw the paint is revealed in the way it spatters, with greater force making longer more slender imprints, for example. Hence, analogical aesthetic communication has the features of smoothness, sensitivity, and dimensionality that we earlier discussed.
Digital coding, however, operates according to isomorphism. Deleuze’s use of the term follows Tarski’s definition, because for Deleuze, an isomorphic reproduction is one with the same internal relationships as its original, even if their corresponding parts look dissimilar (as was the case for the Arabic and Roman numerals).[xxxvii] Isomorphism, we will find, is essential to Deleuze’s discordant coupling of analog and digital.
We could pictorially represent isomorphism with the image below:
Here, the two isomorphic sets are a and b. Set a has three objects, numbers 1, 2, and 3. The relations between each are numerical succession. The objects in set b are three letters a, b, and c; so, the relations between them are alphabetical succession. To be isomorphic, there must be a one-to-one correspondence between the objects of both sets and also between their relations. We see in this image that Tarski’s requirements are fulfilled: both have equivalent and corresponding objects (although they unalike), and the relations between them, succession, are maintained in both sets. This isomorphic relation could be condensed, or coded, if you will, with a simple description such as “three successive variables.” Then, this particular arrangement of relations could be easily communicated, and it can also be ‘translated’ to other forms, for example other alphabets or numerical symbols. Hence, digital aesthetic communication also bears the features of copyability, complexty, and medium independence that we earlier discussed.
Deleuze then describes Francis Bacon’s painting technique which is a “middle way” between analogical and digital, and it communicates disorder of our faculties, such as sense-perception, imagination, conception and so forth (later we explain how this disorder serves the becoming of thought and selfhood). When Bacon first begins to paint, his imagination sees cliché representations on the canvas, and he begins to paint their basic formal features. This is the digital, ordered, optical, and conceptual component of diagramming, because Bacon ‘sees’ on the blank canvass the preformed images that initially pervade his imagination. Yet, before progressing too far, he makes irrational, involuntary, accidental, free, and random ‘asignifying’ marks: he throws paint over the forms, or smears some parts together before the paint dries. This is the analogical, chaotic, manual, and bodily element introducing chance and catastrophe; they are ‘traits’ of confused sensations manually marked by hands acting on their autonomous impulses.[xxxviii] Bacon then ‘surveys’ the random markings as though they were graphs or diagrams that suggest new dimensions and images that he may superpose upon the given forms. By exploring these alternative developments, Bacon deforms his figurations and thereby evokes incompatible images:[xxxix] on account of the deforming and blurring effect of the diagram, incompatible images are forced together, which disorganizes our faculties.[xl]
We may illustrate the way that Bacon's paintings disorganize our faculties by briefly examining Deleuze's critique of Kant’s notion of facultative discord in sublime experiences. For Kant, under normal conditions, our faculty of sensation detects an object that is given to us with extensive magnitudes: it extends in time and space. When we confront an object, we do not grasp its extensive dimensions all at once; for, no matter how small the object, a passage of time is required to scan its full spatial extent.[xli] It is not until we take all the extensive parts together that we comprehend the object, to take it as a whole; but this is done through a succession of apprehensions of the parts which are then retroactively synthesized into a whole. The faculty of imagination does this by reproducing the representations of the previously apprehended parts and then uniting them all into a synthetic representation of the entire object. The faculty of understanding then proceeds to recognize the object by identifying it with its proper concept. This harmonious cooperation of the faculties recognizing a shared object is our ‘common sense.’[xlii]
When experiencing the mathematical sublime, we confront something formless whose extensive magnitude is absolutely great. As such, there can be no end to the succession of apprehensions; and, our imagination, which dually reproduces passing appearances while representing those still appearing, encounters the limit of the amount of representations it may reproduce and synthesize into one object. For example, we might gaze upon a starry night sky; and, when trying to grasp its extent, we continually discover that between each star are more fainter ones, and between those even more. We uncover galaxies in what we previously thought were but single points of light, so that it becomes impossible to assess the night sky’s extent, on account of its infinite depth: even its tiniest parts conceal cosmic expanses that are far beyond our comprehension.
Yet still, we desire the pleasure that results when our faculties fulfill their purpose of comprehension, and thus we add to the violence that the imagination already experiences from its being pushed past its limits, by pressuring the faculties to comprehend the absolutely great object. However, on account of its endless magnitude, the absolutely great object cannot be represented by comprehending its extensive parts. The best the imagination can do is represent the “subjective play of the powers of the mind (imagination and reason) as harmonious even in their contrast.”[xliii] That is to say, our faculties cannot represent the object, but rather only their own failed coordinated efforts to do so. This ‘negative’ representation is then correlated with the faculty of reason’s idea of the absolute whole, and thereby the violence is resolved, and our pain from the sublime experience is replaced by the pleasure of satisfying our purpose as rational creatures.[xliv]
Yet, Deleuze offers a different view of humanity: we do not fulfill our potential when our faculties harmonize by recognizing a common object; rather, our thinking and selfhood are at their peak when internal confusion prevails. When we can find no over-arching idea or story to explain how discordant images cohere – while yet being constrained to do so – then we are learning new things.[xlv] We can have these suspended sublime-like confused experiences when viewing a painting, because we apprehend it in parts, which do not necessarily need to coalesce. If we cannot find a concept that unifies the artwork, then we continue to examine its parts endlessly. Thus, if Bacon can suggest an organization between the parts, while also continually preventing our discovering such a coherence on account of irreducible chaotic elements, then he may achieve the suspended sublime-like experience that confuses our faculties and causes us to learn.
Deleuze details how the diagramming technique serves as Bacon's method for accomplishing this facultative disorder: the diagram produces the deformed image, whose parts do not resemble those of the original, but whose relations between its parts do, and thus it is isomorphic. For example, Bacon says of his 1946 Painting that he originally attempted to paint a bird alighting on a field.
He began by painting the bird’s basic formal features, but then ‘scrubbed’ part of the nascent image, thereby diagramming it. (We see remnants of the diagram in the black and grey smears at lower-center left). Doing so unlocked a series of possibilities for new directions to take the painting, and it set-off a chain of distortions throughout the whole artwork.
What results is a painting whose images in one way are confused, but in another way are coherent. They are confused, because we cannot recognize the objects based on their appearances, nor can we discern how the images relate to each other. As our eyes move from place-to-place on the canvass, it is unclear for example what the skeletal figure is, how and why an umbrella hangs over it, and what sort of an animal corpse would have such an appearance, or why it would be hung in this manner. However, these indeterminate images suggest a coherence, because they are aesthetic analogs of the original bird image: what looks like an umbrella is the aesthetic analog of the original bird’s head, the skull was previously the beak, and the hanging carcass was the wings. It is not that the umbrella resembles a head; rather, the relation between the bird’s head and its beak is somehow analogous to the relation between the umbrella and the skeleton’s skull, although in an indescribable way. As Deleuze writes, “what is substituted for the bird is not another form, but completely different relations, which create the complete Figure as the aesthetic analogue of the bird.”[xlvi]
When viewing a diagrammed painting, we must contend with a suggested form that is forced together with a contrary visual form. Our faculties are compelled to recognize something in the deformed image, because we sense that there is some organization to it, but none can be found on the surface. Deleuze calls these deformed images aesthetic analogies, because our aesthetic experience of the deformed image is analogous to how we would have experienced the original image: if we were looking at the initial bird-form instead, our eyes might have moved around the painting much like they do when viewing the diagramed painting; for, both versions are ‘organized’ the same way. Yet, the deformed appearance causes our faculties to contend with incompatible images. We thereby obtain a sensation that does not result from our being horrified by something we see; but rather, our nervous systems are shocked into confusion by something we are unable to recognize and conceive.
[i] James Blachowicz, “Representation Beyond Mental Imagery,” The Journal of Philosophy, (Vol. 94, No. 2, Feb., 1997), p.62.
[ii] Allen Mornington-West, “Digital theory,” in Sound Recording Practice, Ed. John Borwick, (Oxford: Oxford University Press, 1987), p.36.
[iii] Allen Mornington-West, “Digital Theory,” in Sound Recording Practice, Ed. John Borwick, (Oxford: Oxford University Press, 1987), p.393-409.
[iv] Images from Sean Davies, “Disc Cutting,” in Sound Recording Practice, Ed. John Borwick, (Oxford: Oxford University Press, 1987), p.393-409.
[v] John Haugeland, “Analog and Analog,” in Mind, Brain, and Function, Eds. J.I. Biro and Robert W. Shahan, (Oklahoma: University of Oklahoma Press, 1982), p.220.
[vi] Blachowicz, p.65.
[vii] However, our ears can detect the digitality of higher-frequencies sounds, like those produced by cymbals, because many such faster waves are found between sample-points, and thus too much of their wave-movement is deleted.
[viii] The holes and pits do not themselves alone stand for a 1 or a 0. Instead, a change from a pit to a surface or vice-versa indicates a 1, while no change indicates a 0.
[ix] I must credit Philip K. Dick’s novel Do Androids Dream of Electric Sheep? (which is the basis for the film Blade Runner) for inspiring this paper’s title. His story raises questions about whether computer-intelligences can be treated as human; while, Moravec’s uploading has us wonder if humans can be treated as artificial intelligences.
[x] Haugeland p.213.
[xi] Blachowicz, p.55.
[xii] Nelson Goodman, Languages of Art, An Approach to a Theory of Symbols, (New York: The Bobb’s-Merrill Company, 1968), p.160-161.
[xiii] James H. Moor. “Three Myths of Computer Science,” (The British Journal for the Philosophy of Science, Vol. 29, No. 3, Sep., 1978), p.217.
[xiv] “Seeing, hearing, and smelling are different ways we have of getting information about s to a digital-conversion unit whose function it is to extract pertinent information from the sensory representation for purposes of modifying output. It is the successful conversion of information into digital form that constitutes the essence of cognitive activity. If the information that s is F is never converted from sensory (analog) to a cognitive (digital) form, the system in question has, perhaps, seen, heard, or smelled an s which is F, but it has not seen that it is F – does not know that it is F.... Cognitive activity is the conceptual mobilization of incoming information, and this conceptual treatment is fundamentally a matter of ignoring differences (as irrelevant to an underlying sameness), of going from the concrete to the abstract, of passing from the particular to the general. It is, in short, a matter of making the analog-digital transformation,” Fred Dretske, Knowledge and the Flow of Information, (Cambridge: MIT Press, 1981), p.142.
[xv] “Digital conversion is a process in which irrelevant pieces of information are pruned away and discarded. Until information has been lost, or discarded, an information-processing system has failed to treat different things as essentially the same. It has failed to classify or categorize, failed to generalize, failed to ‘recognize’ the input as being an instance (token) of a more general type,” Dretske, p.141-142.
[xvi] Hava T. Siegelmann, “Neural and Super-Turing Computing,” Minds and Machines, (Vol. 13, Issue 1, February 2003), p.105.
[xvii] Warren S. McCulloch, Embodiments of Mind, (Cambridge: MIT Press, 1988), p.22; 36. Coincidentally, the inclusive disjunction (OR) logic gate can be produced with this arrangement of NAND gates (not both A and B.) Below we compare the nerve arrangement with its logic gate counterpart:
Also coincidentally, the analog-to-digital conversion circuit uses disjunction gates to render the signals into binary coding. Although there are significant differences between the interpretations of both diagrams, we display them here merely to illustrate the resemblance between McCulloch’s depiction of nerve arrangements with the sort of computer logic he had hoped to replicate the brain’s functioning.
[xviii] Siegelmann, p.105.
[xix] Ray Jackendoff, Consciousness and the Computational Mind, (London: MIT Press, 1987), p.33.
[xx] John von Neumann, Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components, Collected Works, A.H. Taub, ed. (New York: Pergamon Press, 1963), Vol. 5, p.372. qtd. in Hubert Dreyfus, What Computers Can’t Do: A Critique of Artificial Intelligence, (London: Harper & Row Publishers, 1968), p.72.
[xxi] Moor, p.218.
[xxii] Dretske, p.143
[xxiii] Siegelmann, p.104.
[xxiv] Gregory Bateson, Steps to an Ecology of Mind, (New York: Ballantine, 1972), p.365-366.
[xxv] Gilles Deleuze, Logic of Sensation, p.79.
[xxvi] Image from: Ralph Abraham and Christopher D. Shaw, Dynamics – The Geometry of Behavior, Part 1: Periodic Behavior, (Santa Cruz: Aerial Press, Inc., 1984), p.15.
[xxvii] “in kinesic and paralinguistic communication, the magnitude of the gesture, the loudness of the voice, the length of the pause, the tension of the muscle, and so forth – these magnitudes commonly correspond (directly or inversely) to magnitudes in the relation that is the subject of discourse,” Bateson, p.373-374.
[xxviii] Bateson, p.372-373.
[xxix] Bateson, p.374.
[xxx] Sérusier, qtd. in Gilles Deleuze, Francis Bacon: Logic of Sensation, Transl. Daniel W. Smith, (
[xxxi] Logic of Sensation, p.73.
[xxxii] Images, Wassily Kandinsky, Kandinsky: Complete Writings on Art, Ed. Kenneth C. Lindsay & Peter Vergo, (Boston: Da Capo Press, 1994), p.520, 655.
[xxxiii] Paul Klee, On Modern Art, Transl. Paul Findlay, (London: Faber & Faber, 1987), p.21. Image, Kandinsky, p.641.
[xxxiv] Logic of Sensation, p.73.
[xxxv] Logic of Sensation, p.76.
[xxxvi] Logic of Sensation, p.73-75.
[xxxvii] Of course, Deleuze’s notion of isomorphism is more general, and does not involve matters of formalized logic or mathematics.
[xxxviii] Logic of Sensation, p.71.
[xxxix] Logic of Sensation, p.27.
[xl] Logic of Sensation, p.60.
[xli] Immanuel Kant, Critique of Pure Reason, Transls. & Eds. Paul Guyer & Allen W. Wood, (Cambridge: Cambridge University Press, 1998), B202-204.
[xlii] Gilles Deleuze, Logic of Sense, Transl. Mark Lester (London: Columbia University Press, 1990, reprinted by Continuum, 2001), p.89.
[xliii] Immanuel Kant, Critique of the Power of Judgment, Transls. & Eds. Paul Guyer & Eric Matthews, (
[xliv] Critique of the Power of Judgment, p.143.
[xlv] Gilles Deleuze, Nietzsche & Philosophy, Transl. Hugh Tomlinson, (New York: Columbia University Press, 1983), p.108.
[xlvi] Logic of Sensation, p.110.
Labels continued at:
http://piratesandrevolutionaries.blogspot.com/2011/07/labels-continuation-for-entry-deleuzes.html


.jpeg)








































































No comments:
Post a Comment