[The following is summary. My commentary is in brackets. Boldface is mine. I apologize in advance for any distracting typos or other errors.]
Summary of
Patrick Suppes
Introduction to Logic
Ch. 11. Functions
§11.2 Operations on Functions
Brief summary:
The converse of a function has for its pairings of outcomes the same as those of the function except with the order of the couples’ members inverted. Note two things. {1} A function can assign many different members of the domain to the same member of the counterdomain. {2} A function cannot assign the same member of the domain to more than one member of the counter domain. Thus the converse of a function may not itself be a function, if the original function assigned more than one member of the domain to the same member of the counterdomain. However, when the converse of a function is in fact itself a function then we call it the inverse and we note it with a superscript ‘–1’. When solving for an inverse function, there are two important principles:
For every x in the domain of f
(I) f–1(f(x)) = x,
and for every x in the range of f
(II) f(f–1(x)) = x.
And a simple, but in some cases flawed, strategy for solving for the inverse has three phases: (i) Substitute ‘
f–1(
x)’ for ‘
x’; (ii) Apply (II);(iii) Solve the resulting equation for ‘
f–1(
x)’.
Summary
[In the prior
section 11.1, we noted that a function is a special kind of binary relation, namely, one that relates to each element in the domain a unique element in the counterdomain. Now recall further from
section 10.6 the notion of a converse relation...
the basic idea is that a binary relation will have its set of ordered couples. The converse relation has the set where all the first one’s couples have their order inverted.]
Besides these operations, which are all simply special cases of the operations on sets, it is also possible to define some special operations on binary relations which depend on the fact that they are sets of ordered couples. The converse of a relation R

is the relation such that, for all x and y, xRy if and only if yRx. Thus the converse of a relation is obtained simply by reversing the order of all the ordered couples which constitute it. The converse of the relation H which holds between x and y if and only if x is the husband of y, is the relation W which holds between y and x if and only if y is the wife of x. Thus,
(Suppes 226)
... So since functions are binary relations, and furthermore, since binary relations can have their converse relations, we can also speak of the converse of a function. Now still even further recall from
section 11.1 the idea that a function can relate many terms in the domain to the same term in the counterdomain. Were it the other way around, and the same term in the domain related to many in the counterdomain, then it would not be a function. For, a function is designed such that a member of the domain gets a unique member in the counterdomain, which means no more than one. So suppose we have a function where more than one member of the domain is assigned to the same member of the counterdomain. Were we to find the converse and switch positions of all the couples’ members, we would then have a situation where the same member of the domain is assigned different members of the counterdomain, and thus the converse of such a function would still be a binary relation, but it will not be a function.]
Since a function is simply a special kind of relation, we can speak of the converse of a function. The converse of a function is always a relation, but in general it will not be a function. |
(Suppes 234-235)
[Suppes then gives another example, namely, f(x)=x2. Now suppose we will render this as a relation whose set is ordered n-tuples. My first thought would be that the ordered tuples for <x, y> would be things like <2, 4>, <3, 9> and so on, because I would think that it would take a number from the domain and assign to it the square of that number. But he says that in this case x = y2. That is probably correct, but I still do not know why, because as I understand it, y = x2, when we take x to be the first number of the couple and y to be the second number which is the square of the first. At any rate, if we keep that structure where the first number comes first in the couple and the second is its square, then the rest of his example makes sense to me.]
A a second example, suppose f is the function such that for every real number x,
f(x)=x2
if we consider f as a relation, <x, y>∈ f if and only if
x = y2.
Consider, now, x = 4. Then
and also <4, –2>∈ f . Hence
is not a function.
(Suppes 235)
And of course the converses of certain functions are still functions too. When the converse of a function is also a function, we say that the converse one is the inverse of the first one, and we use the superscript ‘–1’ to notate it instead of the cup symbol.
On the other hand, some functions are such that their converses are also functions. For example, if g is the function such that for every real number x,
g(x) = 2x + 4.
When a function f is such that its converse relation
is also a function, then we say that
is the inverse of f. To mark this special situation we use ‘–1’ as a superscript in place of the more general cup notation
Thus if the converse of f is a function,
We use the notation ‘–1’ only when
is a function.
(Suppes 235)
[Let us look again at the example:
g(x) = 2x + 4.
(Suppes 235)
So let us suppose that we have for the function among the couples, <2, 12>. For the inverse function, suppose we start with 12, then we take half of it, or 6, and we subtract 2, and so <12, 2>. So let us start with 2. And let us apply it to the function g. So g(2) = 12. Now, let us take that 12, and apply it to g–1. So g–1(12) = 2, which is what we started with. Or another way to write that could be: g–1(g(2)) = 2.]
It should be noticed that when the inverse of f exists (i.e., the converse of f is a function), we have the following identities: For every x in the domain of f
(I) f–1(f(x)) = x,
and for every x in the range of f
(II) f(f–1(x)) = x.
Principles (I) and (II) are both important in solving for f and f–1 as we shall soon see.
(Suppes 235)
Suppes recalls the discussions from the prior
section 11.1 when we spoke of many-one and one-many relations. Suppes explains, “A relation which is both many-one and one-many is
one-one” (235). [I suppose the idea is this. Think of a relation that relates each term in the domain with its own assigned one in the counterdomain. Possibly it is many-one, meaning that more than one item in the domain is assigned the same one in the counterdomain. Suppose also that it is one-many. That means, to each member of the counterdomain is assigned a unique member of the domain. This I think normally means that more than one member of the counterdomain could get various members of the domain. Howeve, since we are combining them, for any term in the domain, there will only be one unique member in the counterdomain it is related to, and likewise, for any in the counterdomain, there is only one in the domain, and furthermore, that relation is the same going both ways. So it is one-one now.]
At the end of the last section we spoke of many-one and one-many relations. A relation which is both many-one and one-many is one-one.
(Suppes 235)
[Furthermore, since a one-one relation is many-one, it is already a function. Suppes will list a number of statements about some relation R, and afterward he will determine which are equivalent.]
We also speak of a one-one relation as a one-one function. Consider now the following statements about a relation R:
(1) R is a function.
(2) R is a many-one relation.
(3) The converse of R is a function.
(4) R is a one-many relation.
(5) R and its converse are both functions.
(6) R is a function and its inverse exists.
(7) R is a many-one relation and R is a one-many relation.
(8) R is a one-one relation.
(9) R is a one-one function.
(Suppes 236)
[Suppes says that 1 and 2 are logically equivalent. So ‘R is a function’ ↔ ‘R is a many-one relation’. We saw this already in the definition of function. A function is one that assigns to a member of the domain a unique member of the counterdomain. 3 and 4 are equivalent, so ‘The converse of R is a function’ ↔ ‘R is a one-many relation’. If the converse is a function, that means to each of the original function’s counterdomain members is assigned a unique member of the domain, and thus the original R relation is a one-many relation. Finally, 5 through 9 are all equivalent. As we see from them, the reasoning for this is found in the definitions and discussions we just had.]
The following equivalences hold:
(1) ↔ (2),
(3) ↔ (4),
(5) ↔ (6) ↔ (7) ↔ (8) ↔ (9).
(Suppes 236)
Suppes now has us suppose that we have a function that is defined by an equation. But we need to know if the function’s inverse exists and if so, what would it be. He gives a technique for making these determinations. So we consider the example:
(1) f(x) = 5x – 4
and x is a real number. There are three phases to this procedure. In the first phase, we substitute f–1(x) for x. In our example, he notes that
Since (1) holds for every real number x, we may substitute ‘f–1(x)’ for ‘x’ (application of universal specification) and obtain:
(2) f(f–1(x)) = 5f–1(x) – 4.
[I did not summarize the section where he discusses universal specification. So see page 59. He defines it there as:
Rule of Universal Specification: US. If a formula S results from a formula R by substituting a term t for every free occurrence of a variable v in R then S is derivable from (v)R.
In the above derivation, the term t is simply ‘x’ in both cases of universal specification, which is why we spoke of dropping quantifiers, but in general | we want to be able to replace the quantified variable by any term. Thus if ‘a’ is the name of John Quincy Adams, we may infer ‘Aa → Ma’, as well as ‘Ay → My’, from ‘(x) (Ax → Mx)’. And in the case of arithmetic from the statement ‘(x)(x + 0 = x)’ we may infer by universal specification ‘(x + y) + 0 = x + y’; in this case the term t is ‘x + y’.
(Suppes 59-60)
So as you can see, to go from the first to the second formula, he simply substitutes ‘f–1(x)’ for cases of ‘x’
(1) f(x) = 5x – 4
(2) f(f–1(x)) = 5f–1(x) – 4.
] The second phase is to apply (II) [Recall that it was: for every x in the range of f
(II) f(f–1(x)) = x.
] So in our formula, anyplace where we see f(f–1(x)) we then place x.
(2) f(f–1(x)) = 5f–1(x) – 4
(3) x = 5f–1(x) – 4
(Suppes 236)
The third phase is to solve this resulting equation for (f–1(x)). [So let us place the formula we need to solve for:
x = 5f–1(x) – 4
We will subtract –5f–1(x) from both sides.
x –5f–1(x) = – 4
We will now subtract x from both sides.
–5f–1(x) =–x – 4
We will now remove the negations by multiplying the terms by negative 1.
5f–1(x) =x + 4
And finally we divide the terms by 5 to finally solve for f–1(x).]
(4)

(Suppes 236)
Suppes then notes a defect with that procedure, namely, that it will “yield an inverse function even though no such inverse may exist” (236). He has us consider:
(5) f(x) = x2 – 1
(Suppes 237)
[The first phase again is to substitute f–1(x) for x.
f(f–1(x)) = f–1(x)2 – 1
The we apply (II)
(II) f(f–1(x)) = x.
to get]
(6) x = f–1(x)2 – 1
[Now let us solve for (f–1(x)). I might get this wrong, but let us start by subtracting f–1(x)2 from both sides.
–f–1(x)2 + x = – 1
Now let us subtract x from both sides.
–f–1(x)2 = –x – 1
We will remove the negations.
f–1(x)2 = x + 1
And we take the square root of both sides to get]
(Suppes 237)
[If we substitute 3 in for x, we get the square root of four, which is two and negative two.]
We thus infer that
f–1(3) = 2 and f–1(3) = –2
and hence
2 = –2
which is absurd.
(Suppes 237)
[Suppes then explains the problem, but I might not follow it well. He says that since the inverse of the function is not a function, that means to one object in the domain it assigns multiple values. So when we had f–1(x) in the equation, it is not a term that we can substitute using universal specification, because that requires the term being substituted to be consistently itself throughout. I think I misunderstand this, so let me quote.]
The mistake here was in inferring (6) from (5). The substitution of ‘f–1(x)’ for ‘x’ is permissible only if ‘f–1(x)’ is a proper term. If f is not a function, the expression ‘f–1(x)’ is not a term, since it does not designate a unique entity.
(Suppes 237)
[Suppes’ next point is very mathematical. He says that mathematicians have a broader meaning for the inverse of a function. I do not follow so well, and I will not give a proper presentation of the ideas. What seems to be going on is the following. A function is a relation whose set is a series of ordered couples. The inverse function would be a set with a series of couples where the couples are the same except the order of each one’s terms is switched. The way that inverses are defined in mathematics seems to be something like the following. The original function will take some objects from the domain, and couple it with another, as if it were a result of an operation. The mathematical inverse is such that were it applied to that function you would get the original term. We saw already how the square of a term complicated our formula, giving us two values for the inverse function, which means it is not really a function. But for mathematical inverses, this does not disqualify it from being an inverse, it seems. So suppose your function is f(x)=x2. This will “output” a series of values, depending on the “input” values. The mathematical inverse needs just to be one that outputs the original series of values. For f(x)=x2 this would be the square root of x. The fact that this function now outputs negated terms along with their non-negated counterparts does not disqualify it. Suppes then discusses the solution they have in mathematics, where apparently they arbitrarily select one value as the ‘principle’ one. This part of the explanation is a too technical for me at the moment. Since this concerns mathematics more than it seems to concern logic, I will not complicate the summary by including it. See pages 237-238 for the details.]
[Suppes will now discuss the relative product of two functions, which is also called the composition of two functions. First recall from
section 10.6 the idea of the relative product of relations...
Relative product of two relations. This operation combines two separate relations by finding ones where the second member of one couple (in the first relation) is the same as the first member of the second couple (in the other relation). From these pairings of couples, you make a new couple that takes the first member of the first couple and the second member of the second couple. Being an aunt is an example, with you and your aunt being the end-terms of separate relations (you being the child of your parent, and your parent being the sibling of your aunt), with your parent being the middle term that gets excluded.
If R and S are binary relations, then by the relative product of R and S (in symbols: R/S) we mean the relation which holds between x and y if and only if there exists a z such that R holds between x and z, and S holds between z and y. Symbolically,
x R/S y ↔ (∃z) (xRz & zSy).
If xPy means that x is a parent of y, and xSy means that x is a sister of y, then x(S/P)y means that there is a z such that x is a sister of z and z is a parent of y, and hence such that x is an aunt of y.
(Suppes 226)
... The basic idea with function composition seems to be that we have two functions. The first function assigns to each member of the domain a unique member of the counterdomain. The second function has for its domain the prior function’s counterdomain, and the second function assigns these objects to yet a new unique member of the second function’s own counterdomain. It could be written f(g(x)) or it can be considered as one whole function like h(x). Suppes will use a notation system where a small circle is used between the two composed functions. Now, suppose we used the relative product notation of the slash to notate this. Suppose we have two functions: (a) f(x) = x + 2 and g(x) = x2. And suppose our composition is of this form: f(g(x)). And for the sake of comparison with relations, let us turn these into ordered couples. We will take x here to be 2. So our first couple is <2, 4>. We then have <4, 6> from function f. Now were we to use the slash formulation, we would keep the structure of <2, 4> / <4, 6> and write it g/f. Suppes says the problem with this is that it is not the right natural order for f(g(x)). So he uses a circle: f ∘ g. Suppes will then say that the composition of functions is associative but not commutative. That it is not commutative would seem to result from the fact that if you change the order of the functions you will get different results and so it is not overall the same function. I am not sure about the associative idea, but perhaps this is for when you have a composition of for example three functions, and were you to compute the value, you could either do the first pair first or the second pair second. However, I do not know how that would work, because I would think you always need to begin with the function that is most nested, as it gives the value for the next function, and so on. Let me quote:]
The relative product of two functions plays an important role in many discussions and is sometimes given a special name: the composition of the functions. Suppose that f and g are functions, and that x, y, and z are entities such that
(7) y = f(z)
and
(8) z = g(x);
then x stands to y in the relation g/f. In other terms, from equations (7) and (8) we see, that
y = f(g(x)).
Thus the relative product, or composition, of two functions is a function h such that (whenever x is in the domain of definition of g, and g(x) is in the domain of definition of f)
h(x) f(g(x)).
This operation of forming the composition of two functions is so extensively used in certain branches of mathematics that various special symbols have been used for it; we shall use a small circle ‘∘’. Thus, (f ∘ g)(x) = f(g(x)). We introduce this special notation instead of using the relative product notation because the order of ‘f’ and ‘g’ in ‘f ∘ g’ is the natural one corre- | sponding to their order in ‘f(g(x))’, whereas this order is reversed in the relative product:
f ∘ g = g/f.
It is clear that composition of functions is associative but not commutative.
(Suppes 238-239)
[Suppes returns now to the problem of finding the inverse. I do not follow this part well. It seems we first should recognize that the inverse is a composition of one function with another such that it produces the same set of ordered couples that the first one produced except with the order of each couple’s members inverted. Were we to think of a term undergoing a transformation through the function and its inverse, we would have that function be assigned to a new one then the new one assigned back to the first.]
The problem of finding the inverse of a function is actually a special case of the problem of finding “the” function g, given the functions f and f ∘ g. In finding the inverse, g is f–1, and
(f ∘ g)(x) = (f ∘f–1)(x) = f (f–1(x)) = x.
(Suppes 239)
[He then says that the function g is not unique. I do not follow these ideas so well. I think he means that g does not assign to x a unique element, but I am not sure. He then says that the problem is to “find at least one function g such that f ∘ g is identical with some given function”. I think the idea is that we have function f. We want to find its inverse, which we will call function g. The next part confuses me, because we now deal with two separate functions, and I do not see how we are trying to find an inverse. Instead, the problem is set up as that we have two functions, f and h, and we want to know, what third function does f need to operate on in order to get h? Suppes will give two techniques for finding such functions. As I do not follow some steps, and also as it seems to be more of a technique for solving mathematical sorts of problems, I will leave this part out of the summary. But for details, see pages 239-240.]
From:
Suppes, Patrick. Introduction to Logic. New York: Van Nostrand Reinhold / Litton Educational, 1957.
.











































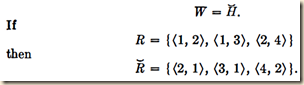




No comments:
Post a Comment