by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Logic & Semantics, Entry Directory]
[Patrick Suppes, entry directory]
[Suppes’ Introduction to Logic, entry directory]
[The following is summary. My commentary is in brackets. Boldface is mine. I apologize in advance for any distracting typos or other errors.]
Summary of
Patrick Suppes
Introduction to Logic
Ch. 10. Relations
§10.5 Ordering Relations
Brief summary:
There are a variety of what are called “ordering relations.” A relation is:
quasi-ordering only if it is both reflexive and transitive;
partial ordering only if is reflexive, antisymmetric, and transitive;
simple ordering only if it is reflexive, antisymmetric, transitive, and connected;
strict partial ordering only if it is asymmetric and transitive;
strict simple ordering only if it is asymmetric, transitive, and connected;
weak ordering only if it is transitive and strongly connected.
Summary
Suppes will define ordering relations, [which are such because in some sense they order the members of the sets]. He distinguishes strong from weak orderings. The stronger sorts, like ≤ and < were discovered first. The other weaker ones are generalizations of stronger ones (Suppes 220).
Orderings do not involve any sorts of relations not already discussed in section 10.3.
A relation is quasi-ordering only if it is both reflexive and transitive. [The “ordering” element here seems to be that it makes every possible pairing of members, but I am not sure.]
A relation R is a quasi-ordering of the set A if and only if R is reflexive and transitive in A. The relation ⊆ of inclusion among sets is an example of a quasi-ordering (of the set of all sets). The relation ≤ is a quasi-ordering of the set of all numbers. The relation of being at least as tall as is a quasi-ordering of the set of all persons. Since all three of these relations have other properties than those of being reflexive and transitive, they are, as we shall see, more than just quasi-orderings. For another example, let
A1 = {1, 2, Robin Hood}
R1 = {⟨1, 1⟩, ⟨2, 2⟩, ⟨Robin Hood, Robin Hood⟩, ⟨1, 2⟩, ⟨2, Robin Hood⟩, ⟨2, 1⟩, ⟨1, Robin Hood⟩}.
Then R1 is a quasi-ordering of A1.
(Suppes 220)
[A relation partially orders a set it seems if it puts the members into pairings in a linear way. The ‘less then or equals to’ relation will make pairings such that a lesser number will always come before a larger number, unless it is the same number paired with itself. So never does a greater number come first. Also, recall the distinction between symmetric, asymmetric, and antisymmetric. It is symmetric of course if for every pairing the relation makes, it can make that pairing in the inverted order. It is asymmetric if in no case does that invertibility hold. And it is antisymmetric if the invertibility holds only whenever the thing is self-related. Recall that Suppes said that ≤ is an example of an antisymmetric relation. ≤ is not symmetric, because although 3 ≤ 3 and 3 ≤ 3, that invertibility does not hold for 2 ≤ 3. It is also not antisymmetric, because although the invertibility does not hold in most cases, it does for 3 ≤ 3. for example. So, it is only symmetric under the condition that both terms are equal to one another. It is thus antisymmetric. ]
A relation R is a partial ordering of the set A if and only if R is reflexive, antisymmetric, and transitive in A. In other words, a partial ordering of A is an antisymmetric quasi-ordering of A. The relations ⊆ and ≤ just mentioned are partial orderings. On the other hand, R1 is not a partial ordering of A1: since it is not antisymmetric in A1: ⟨1, 2⟩ ∈ R1 and ⟨2, 1⟩ ∈ R1, but 1 ≠ 2. Also, the relation of being at least as tall as is not a partial ordering of the set of persons, since two distinct men may have the same height, and thus the relation is not antisymmetric.
(Suppes 221)
[Suppes will then show partial ordering with a Hasse diagram. I am not familiar with this sort of diagram, so it is best to skip to the quotation. My impression is the following. We will see three terms, a, b, and c. There will be an upsloping line going from a to b, and an upsloping line from c to b. But there are no other connections. The fact that if we read the diagram right to left the line between b and c is downsloping seems not matter. What matters is that if we go from one letter to another, the upsloping of that line indicates the directionality of the relation. So this diagram will tell us that the relation holds from a to b, but not from b to a, and it holds from c to b, but not from b to c. It is thus a diagram for partial ordering. Suppes then shows other structures of Hasse diagrams that show partial orderings. One of them is a diamond shape. Let us suppose that the points on the diamond go from a to d, starting with the top one and moving clockwise. This means that we just have these couplings: bRa, cRb, cRd, and dRa. To be reflexive I would think we need things like aRa, but I do not know how that is indicated. But supposing that somehow it is, we might also ask, is antisymmetric? It needs to be symmetric only when a term is self relating. I do not see that indicated in the diagram somehow, but perhaps it is in some way implied in the structure. Is it transitive? I am not sure how. Is it vacuously transitive because the conditional of the formula for transitivity is not fulfilled and thus the whole conditional is true anyway? I am not sure. I will quote as I did not grasp this entirely.]
A partial ordering R of a finite set A may be represented by a Hasse diagram. Small circles represent elements of A and if y may be reached from x by a continually ascending, not necessarily straight line,
(From Suppes 221)
then xRy. For instance, the diagram above represents the partial ordering of a, b, c such that aRb and cRb. R is the set {⟨a, a⟩, ⟨b, b⟩, ⟨c, c⟩, ⟨a, b⟩, ⟨c, b⟩}. Other examples of partial orderings are given by the other diagrams.
(Suppes 221)
[Recall that a relation is connected if it relates any member to any other member.
A relation R is connected in the set A if for every x and y in A, whenever x ≠ y, then xRy or yRx:
R connected in A ↔ (x)(y)(x ∈ A & y ∈ A & x ≠ y → xRy ∨ yRx).
A relation that simply orders a set is one that places them into reflexive, transitive, antisymmetric, and connected relations. So consider ‘less than or equal to’. It is reflexive, since it holds for all numbers in relation to themselves: x≤x, because x=x. It is transitive, because x≤y & y≤z → x≤z. It is antisymmetric, because x≤y but y≰x when x and y are not the same number. However, the pairings are invertible if both x and y are the same number. It is connected, because suppose for example we have the numbers 1, 2, 3, 4. 1≤2, 1≤3, 1≤4. and so on. So the relation connects all of them one way or another. Again, I do not understand the Hasse diagrams. It will place the items in a vertical line. I suppose that the connectivity is implied this way, because we do not see lines going from each one to each other one. In other words, perhaps the idea is that to be further down the vertical chain means to still be related to all those above.]
A relation R is a simple ordering of the set A if and only if R is reflexive, antisymmetric, transitive, and connected in A. In other words, a simple ordering of A is a connected partial ordering of A. The relation ≤ is a simple ordering of the set of all numbers. On the other hand, the relation ⊆ of inclusion is not a simple ordering of the set of all sets, since neither {1} ⊆ {2} nor {2} ⊆ {1}; i.e., since ⊆ is not connected in the set of all sets. None of the above Hasse diagrams represents a simple ordering, since each diagram has at least two elements not connected by an ascending line. In fact, Hasse diagrams of simple orderings are dull. They always look like:
that is, a Hasse diagram of a simple ordering is just a single vertical line.
(Suppes 221)
[The next distinction is between partial ordering and strict partial ordering. I do not grasp the difference so well. Let us walk through the ideas. The first thing we note is that although ⊆ and ≤ are partially ordering relations, and although ⊆ and ≤ are closely related to ⊂ and <, nonetheless ⊂ and < are not partially ordering. I am not certain why, but the two distinguishing features it seems are that ⊂ and < do not allow for reflexivity or antisymmetry, both on account of the fact that the relation does not hold when same term is self-related. But they seem also to have all the other features. Numbers related by < would seem to be transitive and connected for the same reasons that ≤ is. The reasoning for ⊂ not being partially ordering I would think is similar. Recall from section 9.3 that if all the members of one set are included in a second, but not all of the second are included in the first, then we call the first a proper subset of the second, and we symbolize it with ⊂. So as we can see, something cannot be a proper subset of itself, because what would be needed is for one case of itself to have members that the other case of itself does not have. But then it is not the same set anymore. So ⊂ is not reflexive. It is however asymmetric, because the inverted relation holds not even when the term is self-related. And it would seem to be transitive; for, when some first set is wholly contained in a second one, which itself is wholly contained in a third, then the first is also contained in the third. Suppes says that we call relations that are asymmetric and transitive strict partial orderings, and included are < and ⊂.]
The relation ⊂ of proper inclusion and the relation < of less than are closely connected with ⊆ and ≤ respectively, but ⊂ and < are not partial orderings. Since these latter relations are important examples of ordering relations, they suggest the notion of a strict partial ordering. We use the word ‘strict’ because the relation < is sometimes called a strict inequality. Thus a relation R is a strict partial ordering of the set A if and only if R is asymmetric and transitive in A. The relation of being taller than is a strict partial ordering in the set of human beings. It is of some interest to note that the relation of being a husband is a strict partial ordering in the set of human beings. The asymmetric character of the relation is obvious, and the relation is transitive in a vacuous sense, since there are not three individuals x, y, and z such that x is the husband of y and y is the husband of z, for this would require y to be both male and female.
(222)
Suppes then notes that a strict partial ordering is not a more specific type of partial ordering, as if it has one additional qualifying trait. For, strict partial orderings are irreflexive and partial orderings are reflexive. However, Suppes also says that the distinction between them is substantially trivial, as there is always a correspondence between some partial ordering and a strict one, and vice versa; and also, the Hasse diagrams showing such corresponding orderings will be identical (222).
The next distinction is between simple partial orderings and strict simple orderings. [Recall that a relation is simple partial ordering when it is reflexive, antisymmetric, transitive, and connected. And a strict partial ordering is asymmetric and transitive. Now, a strict simple ordering is one that is asymmetric, transitive, and connected. As we can see, it has one feature in addition to those of strict partial orderings, namely, it is connected. Suppes says that < is an example of strict simple ordering, while ≤ is an example of partial ordering. This means that both are transitive. However, ≤ is reflexive (2≤2) and antisymmetric (again, 2≤2), but < is not transitive (2≮2) and asymmetric (in all cases, if x<y, then y≮x).]
The relation between ≤ and < suggested partial orderings and strict partial orderings. It also suggests simple orderings and strict simple orderings. A relation R is a strict simple ordering of the set A if and only if R is asymmetric, transitive, and connected in A. As is to be expected, a strict simple ordering of A is just a connected strict partial ordering of A. The relation < in the set of numbers is a prime example of a strict simple ordering.
(222)
[Recall strong connection: A relation is strongly connected if it holds for any member with any other member and as well with any member and itself.
A relation R is strongly connected in the set A if for every x and y in A, either xRy or yRx:
R strongly connected in A ↔ (x)(y)(x ∈ A & y ∈ A → xRy ∨ yRx).
A weak ordering is one that is both transitive and strongly connected. And recall that a simple ordering is reflexive, antisymmetric, transitive, and connected. And a partial ordering is reflexive, antisymmetric, and transitive. So since simple ordering has all the features of partial ordering, with the inclusion of connected, that means a simple ordering is also a partial ordering. Suppes says that a simple ordering is also a weak ordering. Superficially this is not apparent. A simple ordering has all the features of a weak ordering except being strongly connected. However, a simple ordering is reflexive and connected. And note in the definition of strongly connected above that the relation is strongly connected if it holds for any member with any other member and as well with any member and itself. In other words, if it is reflexive and connected. And recall that a relation is quasi-ordered if it is reflexive and transitive. And again, a weak ordering is transitive and strongly connected. Suppes will show that any weak ordering is a quasi-ordering. I do not follow the reasoning so well, but perhaps the idea is that since strong connectivity involves reflexivity, weak ordering has all the features of quasi-ordering. Let me quote so you can see.]
A relation R is a weak ordering of the set A if and only if R is transitive and strongly connected in A. Since if a relation is reflexive and connected, it is strongly connected, any simple ordering is also a weak ordering, just as any simple ordering is also a partial ordering; but there are weak orderings which are neither partial nor simple orderings-for instance, the relation of being at least as tall as, already mentioned. Also, R1 is a weak ordering of A1. If x = y, then the assumption that xRy or yRx implies that xRx, which leads us to the conclusion that any weak ordering of a set A is also a quasi-ordering of A.
(222)
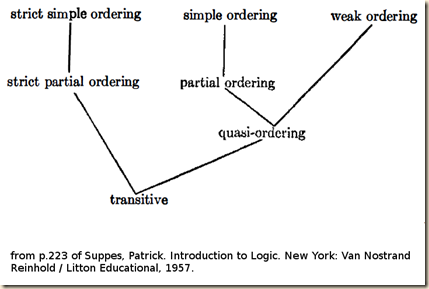
To give a visual representation of these subgrouping relations between the different sorts of orderings, Suppes presents a helpful diagram.
The following diagram makes clear the relations between the various kinds of orderings introduced in this section. When we can pass from one ordering to another by a continuously rising path, this means the second | is a special case of the first. For example, every partial ordering is also a quasi-ordering, but, of course, not every quasi-ordering is a partial ordering. Since all the ordering relations considered in this section are transitive, we make transitive relations the most general case in the diagram.
Sometimes, instead of saying, for instance, that a relation R is a partial ordering of A, it is convenient to say that A is partially ordered by R. Similar terminological remarks apply to the other kinds of ordering.
(Suppes 222-223)
From:
Suppes, Patrick. Introduction to Logic. New York: Van Nostrand Reinhold / Litton Educational, 1957.
.





.jpg)







































No comments:
Post a Comment