by Corry Shores
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Set Theory, entry directory]
[Wikibooks: Set Theory, entry directory]
[My commentary is in brackets.]
Summary of
Wikibooks: Set Theory
Sets
Axioms
Brief summary:
To build up set theory for the purpose of grounding many sorts of mathematics, we need 1) to assume the membership relation along with 2) a number of axioms, namely, the axioms of extensionality (to establish the equality of sets), of empty set (which can be used to build up other sets), of separation (to divide up sets), of pair (to allow sets themselves to be combined), of union (to allow the members of those combined sets to be combined), of power set (to produce from a set yet another set made of all elements of the first set along with all their possible combinations), of infinity (to build up infinite sets on the basis of the empty set and its recurring, nested set containments), of replacement (to allow for a set to be composed by applying a functional/relational operator on the members of some set), and of choice (to allow a set to be made by selecting one member from each of the two-member sets of another set).
Summary
Axioms
Initial definitions
The purpose here is to state the axioms of set theory. Letters will stand for variables that represent “sets in the universe of set theory” [Wikibooks]. We must also assume “the basic property of membership so we can state that x is an element of y. For example, 1 is an element of {0, 1}” [Wikibooks]. At the beginning, we will not use the equality symbol, =, to mean that sets are identical. But after certain axioms, we will be able to do so.
Axioms of Set Theory
[It seems the idea is that we want to select the best axioms for describing set theory and for seeing how other sorts of mathematics are based on it. The most popular set of such axioms are Zermelo-Fraenkel with the Axiom of Choice.]
In order to prove some of the fundamental results of set theory, and to begin to define other branches of mathematics based on it, we need to start with some axioms that we can assume to be true. There are many possibilities for choices of axioms, but the most popular set of axioms is the Zermelo-Fraenkel system, or, more generally, Zermelo-Fraenkel with the Axiom of Choice.
We start by constructing the axiom system known as

[Wikibooks]
[It seems that the following axioms are what make up Z0, and perhaps their order is important. We first need to be able to say when two sets are identical, and we do so by saying that if they have the same members, that is to say, that if they have the same extension, then they are identical sets.]
We’ll need a notion of equality between sets. The following axiom gives that.
[This seems to say that we take into account all possible members for sets A and B. Considering each member, when it is true that they belong in both A and B, then A = B. We might also note that the biconditional is true if both terms are false. Perhaps the idea here is that if we knew all the members of the universe, and we determined that sets A and B both lack exactly the same such members, then they are identical. But I am not sure.]
The next axiom defines the empty set:
We'll define a set that contains nothing:
- Axiom of Empty Set: There is a set X such that for all
 ,
,  .
.
Note that the empty set is written as
or
.
[Wikibooks]
[Let us look at the way it seems to be conceived in this formulation. It seems we are saying that there is a set for which no items whatsoever are included in it, and thus this is the empty set.] [Now, since there is no way to distinguish one empty set from another on the basis of their members (as neither has any to begin with),] “Uniqueness of the empty set follows immediately from the axiom of Extensionality” [Wikibooks]. [Also see Schuller’s proofs for the uniqueness of the empty set.]
[The next axiom seems to want to take some set, then divide it into another set, based on specific properties of the subset’s members. They gave an example previously that might illustrate here: A = {x ∈ R : x2 = 1}. In this example, the idea was that we begin with the set of real numbers, and we select members with a particular property, namely that their square is equal to one. This separates the set of reals into a more exclusive set, in this case, a set containing just one member: {1}.]
Now we need the ability to take a set, and divide up the elements based on whether or not they satisfy some property.
[We learn four other points regarding the axiom of separation. The first is that the separated set is unique, as a result of the axiom of extension. But I am not sure why. I can understand the separated subset being unique within the set from which it was separated, but I would think it could be identical to other sets formed not from that larger set it came from. Perhaps the idea is that were it to be identical with any other set whatsoever, then really they were never two different sets to begin with. But I am not sure. The next point is that the condition cannot be vague, or else it will not precisely define the set. Therefore, we must use mathematical logic to define that condition. The third point is that in fact this is not just one axiom. Rather, there is an axiom for each condition P. For this reason, it is sometimes called the schema of separation. But I do not know why each condition constitutes an axiom in itself, and I also do not know how precisely to distinguish an axiom from a schema. It seems a schema is a formulation or structure of some sort on the basis of which other things of a similar structure can be derived. I am guessing. The last point is that had this axiom been formulated a little differently, it would have fallen victim to Russell’s Paradox. Again, see Schuller for more on how Russell’s paradox conditions the way the axioms are formulated.]
The uniqueness of such a set follows again from the axiom of Extensionality. The condition
must be described precisely using mathematical logic; a vague condition could lead to an ambiguous idea of what the set contains.
Axiom of separation is sometimes called schema of separation, since it comprises infinitely many axioms – one for each condition
. Notice that the restriction
in this axiom helps us to avoid Russell's paradox – in this paradox a “set” of the form
, with
, was used.
[Wikibooks]
And we now give three axioms that allow us to build up new sets from given ones. [It seems the first one is saying that if you have two sets, you can combine them. That would seem to be a union, but there is yet another axiom with that name. Perhaps the difference is the union of pairs contains just their members, but the axiom of pair makes a set whose members are the sets themselves, rather than the combination of the members of those sets. The axiom of union seems to say that if you have a set, then in it is a subset with members of the first set. But I do not understand why it says that the subset’s members are “precisely the elements” of the original set. At least from how it is defined here, I would think that it could be a smaller set. The next axiom which is about power sets seems to say that if you have a set, then you can form another set based on it, which is composed of all the possible subsets made of the sets in the original set.]
The following three axioms are required to generate new sets from given sets.
- Axiom of Pair: If
 and
and  are sets, then there is a set containing exactly
are sets, then there is a set containing exactly  and
and  .
.
- Axiom of Union: If
 is a set, then
is a set, then  is a set. In other words, for any set A, there exists another set whose elements are precisely the elements of the elements of A.
is a set. In other words, for any set A, there exists another set whose elements are precisely the elements of the elements of A.
- Axiom of Power Set: If
 is a set, then there is a set
is a set, then there is a set  so that
so that  each
each  is also in
is also in  .
.
These six axioms, taken together, allow the development of the operations that were discussed in the previous chapter.
[Wikibooks]
Zermelo-Fraenkel
All mathematics agrees on the above six axioms. But we need more axioms in order to “derive certain fundamental results in various branches of mathematics” [Wikibooks]. So we will need to add some, but there is controversy over these additional ones. Together with the above axioms, they are called the Zermelo-Fraenkel axioms (ZF).
The first one that we add is the axiom of infinity, which will allow us to define an infinite set. [Based on what we learned from Schuller, we might say the following about the axiom of infinity. We think of a set containing the empty set. Then we think of that set as well containing the set containing the empty set. Then we further think of that set containing the set containing the set containing the empty set, and so on.]
As we will see, there is no way to define an infinite set given our current axioms, so we require separate axioms for that.
- Axiom of Infinity: An inductive set exists. An inductive set is a set I such that,
 , and
, and  .
.
(Wikibooks)
[The next axiom is the axiom of replacement. Again, drawing from Schuller, we might say that this axiom tells us that a function operating on the members of a set creates another set in its own right. But I am not sure.]
- Axiom of Replacement: If
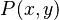 is a property such that for each x, there is a unique y such that
is a property such that for each x, there is a unique y such that 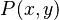 holds, then for every set A there is a set B such that for every
holds, then for every set A there is a set B such that for every 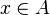 there is a
there is a 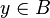 for which
for which 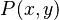 holds.
holds.
Note that like the axiom of separation, the axiom of replacement is often called an axiom schema because there are infinitely many properties
to which such an axiom applies.
[Finally, the axiom of choice first has us consider that we have a set that contains other sets, and these other sets contain pairings of members. The axiom of choice allows us to arbitrarily select one member from each such pair-set to make a new set. Again, my interpretation is based on Schuller’s explanation.]
The Axiom of Choice
The last Axiom in Zermelo-Fraenkel set theory is called the Axiom of Choice. It remains the most controversial axiom among mathematicians, and for that reason, when using ZF with the Axiom of Choice, it is often specified as ZFC.
- Axiom of Choice: For every set S of nonempty disjoint sets, there exists a function f defined on S such that, for each set
 ,
, 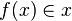 .
.
(Wikibooks)
Source (of text and images):
Wikibooks. “Set Theory/Axioms.” <https://en.wikibooks.org/wiki/Set_Theory/Axioms>
(Accessed 27-03-2016)
.










































 , then
, then 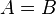
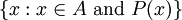 is a set.
is a set.
No comments:
Post a Comment