by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.][Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Set Theory, entry directory]
[Unless otherwise noted, the following is paraphrase and quotation from Schuller, with occassional time codes in brackets referencing the relevant places in the video. Please consult the lectures themselves, since my own presentation is not to be trusted. (Proofreading is incomplete, and I am not trained in this field. So there are many mistakes.) I present it here merely because I will reference parts in future posts. My commentary is in brackets.]
Notes from
Frederic P. Schuller
The Axioms of Axiomatic Set Theory
from Classes 1 and 2 of
“Geometric Anatomy of Theoretical Physics /
Geometrische Anatomie der Theoretischen Physik”
Institute for Quantum Gravity
University of Erlangen-Nürnberg
Brief summary:
We can ground all modern mathematics (and thus all advanced theoretical physics) without making any conceptual assumptions except for the inclusion relation (the epsilon relation or ∈–Relation) in axiomatic set theory. To this concept we add nine axioms which allow us to build up the machinery for the advanced mathematics that theoretical physics uses. To formulate these axioms we need propositional and predicate logic to provide the symbolic language we use. The nine axioms can be abbreviated EE PURP IC F [This overview tries to follow Schuller as closely as possible]:
Basic Existence Axioms
E1: The Axiom on ∈–Relation
∀x ∀y (x∈y) ⊻ ¬(x∈y)
[x∈y is a proposition if and only if x and y are both sets.]
E2: Axiom of Existence of an Empty Set
∃x ∀y : y∉x
There exists a set x such that for all y it is true that y is not an element of x. That is, there exists an empty set, a set that contains no elements.
Construction Axioms
P1: Axiom on Pair Sets
∀x ∀y ∃m ∀u (u∈m ↔ u=x ∨ u=y)
[Let x and y be sets. Then there exists a set that contains as its elements precisely the sets x and y.] [Or: For all x and for all y, there exists a set m, such that for all u, u is an element of m if and only if u is x or u is y.]
U: Axiom on Union Sets
Let x be a set. Then there exists a set u whose elements are precisely the elements of the elements of x.
∀x ∃y ∀c (c ∈ y ↔ ∃z (c ∈ z ∧ z ∈ x))
R: Axiom of Replacement
∃x ∀y ∈ a (∃z A(y, z) → ∃z ∈ x A (y, z)).
Put another way. Let R be a functional relation. Let m be a set. Then the image of m under the functional relation R is again a set.
P2: Axiom on Existence of Power Sets
∀x ∃p ∀y (y ∈ p ↔ ∀z (z∈y → z∈x))
[Put another way. Let m be a set. There exists a set denoted P (m) whose elements are precisely the subsets of m.]
Further Existence/Construction Axioms
I: Axiom of Infinity
∃m (∅∈m ∧ ∀x ∈ m ((x∪{x}) ∈ m)).
There exists a set that contains the empty set and with every of its elements y it also contains the set with the element y (or {y}) as an element.
C: Axiom of Choice
∀X ((∀x ∈ X ∀y ∈ X (x=y ↔ x∩y ≠ ∅)) → ∃z (∀x ∈ X ∃!y y∈ x∩z))
if you have a collection X of pairwise disjoint non-empty sets, then you get a set z which contains one element from each set in the collection. [Schuller, using different formulae: Let x be a set whose elements are non-empty and mutually disjoint, then there exists a set y which contains exactly one element of each element of x.]
Non-Existence Axiom
F: Axiom of Foundation
x≠∅ →∃y (y∈x ∧ y∩x = ∅)
Every nonempty set is disjunct from one of its elements. [Schuller: Every non-empty set x contains an element y that has none of its elements in common with x.]
Summary
Class 1: “Logic of Propositions and Predicates”
For the sake of providing the mathematical foundation for various fields in theoretical physics, Schuller in this class will work toward an account of differential geometry from the most basic concepts possible. This field of mathematics works with space, and space is made of sets of points. So to study these things, we first will need to look at what sets are. But set theory itself cannot be the absolute foundation of this project. For, were we to try to define a set, for example as a collection of elements, we would need already some other concepts (which presumably we cannot assume at this foundational level); for example, how do we define a “collection” and an “element”? The way we will get around this is by constructing set theory on the basis of axioms rather than on such definitions. But in order to formulate these axioms, we first need a language, in this case, of propositional and predicate logic. [Note, while it may seem that Schuller will define the terms or concepts in propositional and predicate logic, he in fact uses a logical operator, the biconditional, which is understood merely in terms of its truth functionality, and what is being biconditionally combined are most basically just mechanically operable symbols.]
What could the first definition be? For a definition you need notions that you already have in order to define a new notion. But if you do not have any notion yet, how would you start? The trick is to start axiomatically, and so we will have to write out axiomatic set theory. But that then raises the question, in what language would you possibly do that? So, actually before we come to set theory, we need another building block down here, and that would be logic. And we will deal with propositional and predicate logic first. That will define our language. Then we will be able to write down the axioms of set theory. (quoting Schuller, 0.08.30 - 0.09.15)
Chapter 1: Axiomatic Set Theory
1.1 Propositional Logic
Def. A proposition p is a variable that can take the values “true” or “false”. No others. [19.30]
We can build new propositions from given ones. We do so by means of logical operators. They come in different forms. The simplest are:
a) unary operators, of which there are four. It takes one proposition p as given, and makes from it a new proposition. This one proposition can have values true or false.
a1) The first is not, ¬. It makes a true value false and a false value true.
b) The second is identity, which we will call ID p. This keeps the same values as p.
3) The third is the tautology operator, ⊤p. It is always true independent of p’s original values.
4) The fourth is the contradiction, ⊥p. Regardless of p’s original value, ⊥p is always false. [23.00]
b) The binary operators. We start with two propositions that we assume as given.
b1) “And,” p∧q. It is a new proposition. In total it is one proposition. It is true only when p and q are true.
There are in fact 16 total such possibilities for binary operators.
b2) “Or,” ∨. [True if at least one disjunct is true]
b3) Exclusive or. [True if either disjunct is true, but false if both or neither.]
b4) Implication arrow →. It takes a proposition and another, and makes a new one out of them. It is false only when the consequent is false and the antecedent true. This means that if the antecedent is false, then the whole implication is true.
b5) Equivalence ↔ [True when both terms are either both true or both false].
[Note, more on the binary operators can be found in many sources.]
Schuller then gives some remarks:
1) We agree on decreasing binding strength in the sequence in this order: ¬, ∧, ∨, →, ↔ .
2) All higher order operators can be built from one single binary operator, namely the NAND operator (negated ‘and’). It is true only when both conjuncts are false. [0.35.20]
1.2 Predicate Logic [0.37.00]
Def.: A predicate is a proposition-valued function of some variable(s). Take one example:
P(x)
Its truth value depends on what x is. Take another example:
P(x, y)
Its truth value depends on what the combination of x and y is.
We can construct new predicates from given ones.
a) We can combine a single predicate with a double to get a predicate for three variables. Q(x,y,z)↔P(x)∧R(y,z)
b) We can convert the predicate P of one variable into a proposition, namely:
∀x: P(x)
The proposition is that formula above. It was constructed form a predicate of one variable: P(x). And we may read it, “For all x, p of x is true”. It is defined to be true if P(x) is true independently of x. [Written on the board: defined to be true, if P(x) ↔ true, independently of x.]
Feel good example:
P(x) is defined as “x is a human being” implies “x has been created.”
[Written on the board as: P(x) ↔ (“x is a human being” → “x has been created.”)]
Then ∀x: P(x) is true.
b2) Existence quantification. It takes a proposition of one variable, and it reads, “there exists an x such that P(x)”.
∃x: P(x)
It is defined in the following way:
∃x: P(x) ↔ ¬(∀x: ¬P(x))
Corollary:
For all x, something is not true is equivalent to it is not true that there exists an x for which it is true.
∀x: ¬P(x) ↔ ∃x: P(x)
If something is not true for any x, then certainly it is not true that there exists one where it is true. [49.30]
Remark:
Quantification for more predicates of more than one variable:
Q(y) ↔ ∀x: P(x,y)
In the above, the x is the “bound variable”. The y, which survived the quantification and which appears again, we call the “free variable”.
We can then quantify again for y.
Remark 2: The order of quantification matters. So for all x, there exists a y such that P(x,y) [or ∀x: ∃x: P(x,y)] is generically different proposition than there exists a y such that for all x, P (x,y) [or ∃x: ∀x: P(x,y).]
1.3 Axiomatic Systems & Theory of Proofs
We need the valid rules for writing a proof.
Def. An axiomatic system is a finite sequence of propositions a1, a2, ..., aN, which are called axioms.
(Note that at this point, we have not defined sets, and therefore we do not really have the numbers that were used as subscripts above. However, instead of these numbers we can use “pre-mathematical scripts”, like hash marks.)
Def. A proof of a proposition p within an axiomatic system a1, a2, ..., aN, is a finite sequence of propositions q1, q2, ..., qM, such that the final qM proposition is the one you want to prove
[Note, there is a cut in the recording here. Perhaps there is also some small measure of conceptual continuity that is lost too, but I am not sure. (1.02.30)]
Remarks:
A proof is a finite sequence of propositions q1 to qM, such that for any j that lies between 1 and the final step, 1 ≤ j ≤ M, that is, for any step of the proof, either of the following condition is true:
(A) qj is a proposition from the list of axioms. This means that an arbitrary step in the proof, we may pick one of the axioms and put it there. [(A) stands for ‘axiomatic’]
or
(T) The jth step of the proof, qj, is a tautology, which is a proposition/statement that is always true independent of the elementary propositions making it up, e.g., p∨¬p. This is always true (you can check a truth table to see this): (p∨¬p)↔⊤ . [(T) stands for ‘tautology’]
or
(M) for the jth step of the proof, qj , there exists for the proof m or n coming before qj, such that the proposition qm and qn implies the jth step, such that this (the prior formulation) is true.
∃ 1 ≤ m,n ≤ j: (qm ∧ qn → qj) is true.
[(M) stands for ‘modus ponens’]
So we could have steps coming before in the proof, and their conjunction implies the jth step is true.
Later Schuller will give one example of this sort of proof scheme, namely, the proof, the uniqueness of the empty set. The other proofs will be abbreviated.
Remark: If p can be proven from an axiomatic system a1, ..., aN, we often write a1, ..., aN ⊢p, and this symbol means “proves”.
Remark: This definition of proof allows to easily recognize a proof. An altogether different matter is to find a proof for a certain proposition.
Remark: Obviously, any tautology, should it occur in the axioms, can be removed from the list of axioms without impairing the power of the axiomatic system. An extreme case of this is: the axiomatic system for propositional logic, which is the empty sequence. For, in propositional logic, all we can prove are tautologies. Thus we have no axioms.
Def. An axiomatic system is consistent if there exists a proposition q which cannot be proven from the axiomatic system: ¬(a1, ..., aN ⊢q) .
The idea behind this definition: Consider an axiomatic system containing contradictory propositions. For instance we have a series of propositions, then we have s, and later on we have not s.
..., s, ...., ¬s, ....
We can conjoin them and imply q.
s∧¬s→q.
Then by the deduction rule (M) clearly:
This is a tautology, because s and not s is always false, and if the assumption (antecedent) is always false, then the whole implication is always true. This means that from any contradiction we can prove any arbitrary proposition. [So this is a bad situation that would indicate that the proof is inconsistent. Now, recall the definition from before: “An axiomatic system is consistent if there exists a proposition q which cannot be proven from the axiomatic system: ¬ (a1, ..., aN ⊢q)” The idea seems to be the following. If it is inconsistent, you can prove all propositions. But if there is at least one that cannot be proven, then it is not inconsistent, and is therefore consistent.]
“So the problem is that any statement can be proven if you have contradictory assumptions, contradictory axioms. Now, it is a sign of not having inconsistency, of not having contradictory axioms, if it is simply not true that every statement can be proven.” [1.22.10]
Theorem: Propositional logic is consistent.
Proof: It suffices to show that there exists a proposition that cannot be proven propositional logic.
Propositional logic has an empty sequence of axioms. So only (T) and (M) must carry any proof.
So we can only add tautologies, and modus ponens only can operate on tautologies. So the only thing we can prove are tautologies. But that means q and ¬q cannot be proven, because it is not a tautology. Thus propositional logic is consistent.
But with other axiomatic systems, proving consistency can be very difficult. Gödel even shows that under certain circumstances, this is impossible to prove. Schuller will give a rough outline of one of Gödel’s theorems.
Theorem: (Gödel)
Any axiomatic system that is powerful enough to encode the elementary arithmetic of natural numbers is either inconsistent or contains a proposition that can neither be proven nor disproven. So it in that case would contain true statements that cannot be proven.
This sent shockwaves through mathematics, because the notion of truth seemed clear. Something is true if it can be proven, based on a system of assumptions. This is the pure truth of mathematics.
Proof: It is complicated.
Basic idea of the proof:
(1) Assign to each (meta-) mathematical statement a number, now called Gödel-number. For example, consider a mathematical statement. Every symbol in the equation gets a number. [Then metamathematically you somehow combine the coding numbers to get one large number for each mathematical statement, I think. See (1.32.00)] Then you have a number for everything, which requires elementary arithmetic computation.
(2) Use a “The barber shaves all people in his village who do not shave themselves”-type argument to identify a proposition that is neither provable nor disprovable. You use some reflexive construction. [Schuller then seems to mention diagonalization (1.34.30). See this entry. Schuller seems to be saying that we use a diagonalizing method to produce a number not in a previous set, then we give that number a Gödel code. “Then you produce a statement that uses the Gödel number of the very same statement. And then you arise at such a contradiction.” I do not follow so well, but I guess the idea is that you begin with a liar-like paradox of self-reference, then you encode it so that it can mathematically refer to its own self in a self-contradictory way. But since this self contradiction is happening all on the level of mathematics, that is problematic, because mathematics is not supposed to do that.]
As we will see next class, everything in set theory is based on the element symbol, which is a predicate of two variables. There is no other predicate of two variables in set theory. Even equality is based on the element symbol. But we never get an explanation of what it means for x to be an element of y. And in fact, given this basic foundation, there is no a priori reason you cannot ask if a set is included in itself. We also learn that the only set you need to construct is the empty set, and all others will be based on it. We will learn the 9 or so axioms that reproduce the set theory upon which all modern mathematics is built.
Class 2: “Axioms of Set Theory”
1.4 The ∈-Relation
Set theory is built on the postulate that there is a fundamental relation (i.e., a predicate of two variables) called ∈ (epsilon).
But we cannot have any preconceived notions about ∈. There will be no definitions of what ∈ is (apart from it being some predicate of two variables) or of what a set is.
We will not make definitions saying something like “a set is ...”. Rather, we will use 9 axioms that speak of ∈ and sets.
These axioms will teach us how to use ∈ and what constitutes a set. So it will only be the interplay between the ∈ and what we call ‘sets’ which defines what a set is and which defines what the ∈ means. Such an approach is necessary if we want to write down mathematics from scratch, without any prior notions or terms, on the basis of which we could define the element relation or set.
Overview of the axioms:
Schuller memorizes them as EE PURP IC F
E, E: Basic existence axioms.
PURP: Construction axioms, which instruct us how to build new sets, once we have given sets.
IC: Further existence axioms, but they can also be classified as construction axioms.
F: (Axiom of foundation) A non-existence axiom that says, “don’t use sets of the following kind.”
[0.06.30]
We will introduce some new relations.
Using the element relation, ∈-relation, we can immediately define further relations. One is x is not an element of y,
x∉y
We see that a relation is a symbol that eats two variables.
∉(x,y) =: x∉y
[Note, I do not know yet what the symbol =: means. Wolfram says this about a similar looking symbol, in their entry for the colon: As a part of the symbol A : = B sometimes used to mean " A is defined as B." ]
But it is tradition to put the symbol between the two variables, because it saves the brackets and comma.
We define this to be equivalent to be not x in y [8.35]:
∉(x,y) =: x∉y : ↔ ¬(x∈y)
And we define a subset relation,
x⊆y
which is defined to be the case if for all a, it is true that a in x implies a in y.
x⊆y :↔ ∀a: (a∈x→a∈y)
And we define x equals y (and so we see the equality sign) is actually defined in terms of the epsilon relation. x equals y means that x is a subset of y and y is a subset of x.
x=y :↔ x⊆y ∧ y⊆x
1.5 Zermelo-Fraenkel Axioms of Set Theory
Axiom E1:
Axiom on the ∈-relation
The first axiom describes the relation between ∈ and sets.
x element y (x∈y) is a proposition (that means it is either true or false) if and only if x and y are both sets.
[11.30]
[Later he gives a formal rendition of this axiom: For all x and for all y, x element y is either/or (exclusive or) true or it is false.
∀x : ∀y : (x∈y) ⊻ ¬(x∈y)
[25.45]
(Note, I am not familiar with his sign for exclusive disjunction, so I typed it with ⊻. It would mean in this case that either x is a member of y or it is not, and it cannot be neither or both. I am not sure how this formulation captures what he says about x∈y being a proposition if and only if x and y are both sets. This new formulation seems to just establish that y is a set.]
We recall from first order predicate logic that we leave it entirely open the nature of the variables that enter such relations as x∈y, which is a predicate of two variables. This first axiom clarifies that x∈y is a proposition if it acts on what we are going to call ‘sets’. This is the first thing we know about sets.
We now give a counter-example showing what is not a set.
Counter-example:
Assume there is an object u, some u, that contains all sets that do not contain themselves as an element . To be precise: we assume there exists a unique u such that for all z, we have z in u if and only if z is not in z; that is, all those sets in u that do not contain themselves.
∃u : ∀z : (z∈u↔z∉z)
[0.14.00]
We assume z is a set, and we assume there is such a u.
Question: is u a set?
Now, consider this part of the formulation: z∉z. We might be bothered, because we normally distinguish a set from the elements of a set. And it may bother us that here we have a set either being an element of itself or not being so. Later we encounter another axiom that will say to ignore such cases. But for right now, in accordance with an above axiom that if we have the ∈-relation x∈y, if x and y are sets, then x∈y is a proposition. Therefore, z∉z is a proposition, because z is a set.
Returning to the question, (is u a set?), we see that it is not. Consider if u were a set. Then one must be able to decide whether u in u (u∈u) is true or false. Why? If u∈u is a proposition, then it must be either true or false.
But
1) assume that u∈u is true
2) assume that u∈u is false
It must be that one of the two options is the case, because u is defined. [Before we continue with the reasoning, let us look again at the formulation at hand:
∃u : ∀z : (z∈u↔z∉z)
The part that reads z∈u would mean that u is a set, because something is included in it. So u would be a set with members z. But the next part of the formulation z∉z says that these members of u do not include themselves. So u is a set of other sets that do not include themselves. We are then wondering, is u itself one of the z that is included in itself.] Let us evaluate the two assumptions.
1) So assume u∈u is true. This means that it is true that u is an element of itself [that is, it fulfills the first part of the formulation z∈u, because u would be a z included in u. So u∈u makes the first side of the biconditional true. But, by making the first part of the biconditional true, that implies the second part is true, which reads z∉z. We are saying that u is such a z, and here that this z (or u) is not included in itself.] So, it immediately follows from the definition of u that u is not in u.
This is a contradiction. If we assume u is in u, it implies u is not in u. So our assumption is false.
2) assume u∈u is false. This is equivalent to saying that u is not in u (or u∉u). [So recall that we are asking if u is an x in the formula
∃u : ∀z : (z∈u↔z∉z)
Since u is not included in u, then it fulfills the second side of the biconditional z∉z. But by affirming the truth of one side of the biconditional we have done the same to the other side, which says that z (which is now taken to be u) is in fact a member of u (or z∈u and thus u∈u). So it follows from the definition of u that u is an element of u, which contradicts our original assumption that it is not. Thus this assumption is also false.
Conclusion: u is not a set. [That is, the set of sets which do not include themselves is not itself a set, because defining it as such leads to a contradiction.]
[0.18.30]
This of course is Russell’s paradox. The ZF axioms help avoid these problems.
Axiom E2:
Axiom of Existence of an Empty Set.
There exists a set that contains no elements.
There exists a set x such that for all y it is true that y is not an element of x.
∃x : ∀y : y∉x
Theorem: There is only one empty set. And because there is only 1, we can give it a name. Call it, ∅.
[00.24.40]
There are two proofs.
Proof: (standard textbook style)
Assume x and x′ are both empty sets. (We will show that any two empty sets are equal and therefore there is only one.) If that is true, then we can write something like: y∈x. But this is false, because x has no members. But since it is false, that means we can make an implication where any consequent is false. So we can write:
(y∈x) → (y∈x′)
But if this is true, that means it is true independently of what y is. But that means we can use the all quantor [I am not sure I get that step. I guess the idea is that it is true regardless of what y is, and therefore it is true for all y.]
∀y : (y∈x) → (y∈x′)
But that just means by definition that x is a subset of x′. [Recall our definition of subset: x⊆y :↔ ∀a: (a∈x→a∈y). This means that if we go with our formulation above, x is a subset of x′, because members of x are members of x′.]
Conversely: we can write,
(y∈x′) → (y∈x)
[y∈x′ is false, so we can make it the antecedent to a conditional with an arbitrary consequent. The whole implication will still be true.] And since it is true independently of y, we can write:
∀y : (y∈x′) → (y∈x)
But this means, x′ is a subset of x. [See the above reasoning.]
x′⊆x
[Now, recall our definition for x=y:
x=y :↔ x⊆y ∧ y⊆x
]
In summary: x=x′
So if you take any two empty sets, they must be the same. So there is only one empty set.
[0.28.30]
Proof: (formal version)
For the formal version, we need to encode our assumptions as axioms (notated a1, a2, etc.). The assumptions are that x and x′ are both empty sets.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
Now we need a string of further propositions (notated q1, q2, etc.). We eventually want to arrive at the statement we want to prove, which is the statement that x=x′.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔
q2 ↔
...
...
qM ↔ x=x′
We will use the three deduction rules (A), (T), and (M) to justify each step.
We first write a tautology: if for all y, y is not an element of x, that implies that for all y, y is an element of x implies y is not an element of x′.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔
...
...
qM ↔ x=x′
Why is this true? We know from the assumptions that this is true: (y∈x → y∈x′). [For, both sides of the implication are false.] Now, since it is true (and since it is the consequent of the larger implication), we know that ∀y : y∉x → ∀y : (y∈x → y∈x′) must be true. [It is a tautology, because no truth assignment can make it false. Let as make these substitutions: p=y∈x, ~p=y∉x, q=y∈x′, ~p=y∉x′. Here is a truth table for what might be the structure of the formulation:
(made with Michael Rieppel’s online truth table generator)
As we can see, there is no truth assignment that makes this proposition false.]
Now we pull the first axiom and we write, q2 is the schema/proposition that for all y, y is not in x.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔ ∀y : y∉x ... [A]
...
...
qM ↔ x=x′
Then for q3, we use modus ponens. We take two prior steps of the proof q1 and q2, and we put an ‘and’ between them. We can then say that this conjunction implies q3 if it is a tautology. [0.34.20] [So we take q1, and we use it to affirm the antecedent in q2, which allows us to affirm the consequent, namely, ∀y : (y∈x → y∈x′), which we then place as q3.]
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔ ∀y : y∉x ... [A]
q3 ↔ ∀y : (y∈x → y∈x′) ... [M]
...
qM ↔ x=x′
But we know from our definitions before that ∀y : (y∈x → y∈x′) is another way to say that x is a subset of x′.
[0.36.50]
For q4, we write a tautology. For all y, y not an element of x′ implies for all y, y in x′ implies y in x.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔ ∀y : y∉x ... [A]
q3 ↔ ∀y : (y∈x → y∈x′) ... [M]
q4 ↔ ∀y : y∉x′ → ∀y : (y∈x′→ y∈x) ... [T]
...
qM ↔ x=x′
[Using the same substitutions as before, we would get the following truth table, which shows it is a tautology.
(made with Michael Rieppel’s online truth table generator)
]
For q5, we pull axiom 2, which was that for all y, y is not in x′.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔ ∀y : y∉x ... [A]
q3 ↔ ∀y : (y∈x → y∈x′) ... [M]
q4 ↔ ∀y : y∉x′ → ∀y : (y∈x′→ y∈x) ... [T]
q5 ↔ ∀y : y∉x′ ... [A]
...
qM ↔ x=x′
Then for q6 we can now conclude q6 is a valid step of the proof, if it has the form for all y, y in x′ implies y in x.
a1 ↔ ∀y : y∉x
a2 ↔ ∀y : y∉x′
q1 ↔ ∀y : y∉x → ∀y : (y∈x → y∈x′) ... [T]
q2 ↔ ∀y : y∉x ... [A]
q3 ↔ ∀y : (y∈x → y∈x′) ... [M]
q4 ↔ ∀y : y∉x′ → ∀y : (y∈x′→ y∈x) ... [T]
q5 ↔ ∀y : y∉x′ ... [A]
q6 ↔ ∀y : (y∈x′ → y∈x) ... [M]
qM ↔ x=x′
[For this step, q6, we take q4, or ∀y : y∉x′ → ∀y : (y∈x′→ y∈x), and we affirm its antecedent with q5, and we thus conclude by modus ponens that ∀y : (y∈x′ → y∈x).] Now, we recall that this is another way to write: x ′⊆x.
[He then says we use modus ponens on q3 and q6 to get the conclusion. But I do not see how either can affirm an antecedent in the other. I also do not see a way to just affirm the antecedent in either one using other steps. The only reasoning I can find for how we get to the conclusion is the definition for the equality of sets. x=y :↔ x⊆y ∧ y⊆x. But for the proof to work, we need modus ponens. I failed to understand this proof, and I invite corrections. At around 0.38.00 he seems to be saying that q6 implying q3 is a tautology, and thus we can write the conclusion (he points to x′⊆x then to x⊆x′ then to the x′ of x=x′. But I do not know what he means there, because I would not know how to make a truth table for all those parts.]
[0.38.45]
Axiom P1:
Axiom on Pair Sets
Let x and y be sets. Then there exists a set that contains as its elements precisely the sets x and y.
What is important is that their combination of sets makes another set.
For all x and for all y, there exists a set m, such that for all u, u is an element of m if and only if u is x or u is y.
∀x : ∀y : ∃m : ∀u : (u∈m ↔ u=x ∨ u=y)
Restated: For any sets, there exists a set such that its elements are precisely those that are either x or y. [This seems to be saying that if you have sets x and y, then you have the set m which is their combination.]
Notation: denote this set m by {x, y}.
[0.43.25]
What the axiom assures us of, is that if x is a set and y is a set, then this whole thing counts as a set.
Worry: Is {x, y} the same as {y, x}?
Yes it is. No worries. This is because, if a comes from {x, y}, then a comes from {y, x}. And if a comes from {y, x}, that means a comes from {x, y}. This means the set {x, y} is a subset of {y, x} and vice versa. So in total they are the same.
[0.45.00]
Remark/Def.: The pair set axiom also guarantees the existence of sets of one element. If we write set x:
{x}
Then we define the set x as the pair set of x with x.
{x} := {x, x}
[0.46.15]
Axiom U:
Axiom on Union Sets
Let x be a set. Then there exists a set u whose elements are precisely the elements of the elements of x.
[Schuller says that he will no longer render the axioms into first order predicate logic statements of the sort we have been making. For that reason, I cannot trust the renditions I try to make. But we should attempt something, and I will base them on other sources. The wiki page for this axiom shows it as.

They translate this as: “Given any set A, there is a set B such that, for any element c, c is a member of B if and only if there is a set D such that c is a member of D and D is a member of A.” Or more simply, “For any set A, there is a set UA which consists of just the elements of that set.” (Wiki) The formula is very complicated. We apparently want to speak of two sets, A and another set with exactly the same members as A. I do not know why we have two other sets mentioned, B and D, rather than just one. At any rate, we learn that members c are in all three sets. The members are in set B if and only if they are in D, which is a set that is in A. To make this formulation look more like the other Schuller has given, perhaps we could write it as:
∀x : ∃y : ∀c : (c ∈ y ↔ ∃z (c ∈ z ∧ z ∈ x))
]
We might be concerned with the definition as Schuller gave it, because we are speaking of union, but we mentioned only one set, x. [Recall he said: “Let x be a set. Then there exists a set u whose elements are precisely the elements of the elements of x.”] He explains that the set x is already the collection of all the sets that will be put into the union.
Notation: The set u is written with a big cup u.
u = ∪x
Ex. Let a, b be sets. [First recall the pair set axiom: “Let x and y be sets. Then there exists a set that contains as its elements precisely the sets x and y.” In the following, he seems to be saying that from set a we can derive {a}, which I guess is the set containing set a, and we do this on the basis of the pair set. Perhaps this is because we consider a to be both members of the pair, but I am not sure.] Take the set with the element {a}, and take the set {b}, and we can put them together into a set: {{a}, {b}}, and we call it x. This is guaranteed by the pair set axiom. We then ask, what is the union of x? ∪x = ? As we said, the union of x is the set that contains precisely the elements of the elements of x. The elements of x are the set with the element a and the set with the element b [that is, the two internal bracketed sets of a and b], so the union of x is the set {a, b}.
[Let us return to the formulation again:
∀x : ∃y : ∀c : (c ∈ y ↔ ∃z (c ∈ z ∧ z ∈ x))
And let us stick with our above a, b example. So the c would be in the example the a and the b, the elements of the sets (these elements are of course themselves sets). The y set I think could be the final union, which was {a, b} in the example. The set z I think would be the internal set containing the set of either a or b. So in {{a}, {b}}, which was made with the axiom of pairing, the {a} and the {b} would be sets z in the formulation. That would make{{a}, {b}} then be set x in the formulation, since a (or c) is contained in set {a} (or set z), and {a} (or set z) is contained in x {or set {{a},{b}}. With that inclusion being true, {a} (or set c) is included in {a, b} (or set y).]
Ex.2: We know that if we start with the set
x = {{a}, {b, c}}
Then we know by the union set axiom that ∪x is a set. And it deserves a name. So we define ∪x as {a, b, c}, and we define it from two element sets. This second example immediately generalizes to a definition.
Def: Let a1, a2, ..., aN be sets. Then define recursively for all N≥3,
{a1, a2, ..., aN } := ∪ {{a1, ..., aN-1 }, {aN }}
Note, Russell’s paradoxical set cannot be such a union. So we can only build a union of as many sets as can fit into a set. If we take all the sets that cannot contain themselves, we cannot collect them in a union.
Axiom R:
Axiom of Replacement
Let R be a functional relation. Let m be a set. Then the image of m under the functional relation R is again a set.
[Note, Schuller will speak of there existing precisely an x. And he uses this symbol: ∃! . But he assigns it for homework to figure out how to understand it. The following I copy from James Aspnes webpage.
3.4.1. Uniqueness
An occasionally useful abbreviation is ∃!x P(x), which stands for “there exists a unique x such that P(x).” This is short for
(∃x P(x)) ∧ (∀x∀y P(x) ∧ P(y) ⇒ x = y).
An example is ∃!x x+1 = 12. To prove this we’d have to show not only that there is some x for which x+1 = 12 (11 comes to mind), but that if we have any two values x and y such that x+1 = 12 and y+1 = 12, then x=y (this is not hard to do). So the exclamation point encodes quite a bit of extra work, which is why we usually hope that ∃x x+1 = 12 is good enough.
(James Aspnes)
]
Def.1 (for functional relation): Relation R is called functional if for every x there exists precisely one y such that R of x and y. Or written more symbolically:
Relation R is called functional if ∀x ∃!y : R (x, y)
This is a function. To every x there is precisely one y. For another x, there is another y. Note that at this state there is no talk about x or y having to be a set.
Def.2 (for image): The image of a set m under a functional relation R consists of all those y for which there is an x∈m such that R (x, y).
[I am not sure from this definition, but the image of set m seems to be all those terms that result when we apply a function to some set of terms.]
We will normally need to evoke a principle based on this axiom called the principle of restricted comprehension.
[1.06.30]
The axiom of replacement implies, but is not implied by, the principle of restricted comprehension.
Principle of restricted comprehension:
Let P be a variable of one variable. And let m be a set. Then, those elements y∈m for which P(y) holds (is true) constitute a set.
Notation: This set is usually denoted the set that contains those y in m for which p of y holds.
{y∈m | P(y)}
We do this all the time. We say, select those elements for which a condition applies. But, this is not consistent.
The Principle of Restricted Comprehension (PRC) is not to be confused with the INCONSISTENT Principle of Universal Comprehension (“P”UC) that Russell had problems with, which is stated, collect all the y for which p of y applies, is a set. But this is not true [Schuller writes (sic)].
{y | P(y)} is a set (sic)
But this is too much, because P of y could be y that is not an element of y.
The difference is that we need to say from the start we name a set m from which they are selected. We already assumed the m, and then the P(y) cannot make it bigger. The m is the restricting part.
Schuller then proves it from the axiom of replacement. [I omit this part, but it can be found at 1.11.45 – 11.17.00]
We will use restricted comprehension to define the complement.
Def: Let u be a subset of m, then m without u is the collection of all those elements of m for which x does not lie in u. More symbolically:
Let u ⊆ m. Then
m\u := {x∈m | x∉u}
We know that {x∈m | x∉u} is a set, due to PRC, that is ultimately due to axiom of replacement.
[Schuller leaves establishing intersection for homework.]
[1.19.15]
[At this point we might want a formula for the axiom of replacement. Wolfram says the following:
Axiom of Replacement. One of the Zermelo-Fraenkel axioms which asserts the existence for any set a of a set x such that, for any y of a, if there exists a z satisfying A (y, z), then such z exists in x,
∃x ∀y ∈ a (∃z A(y, z) → ∃z ∈ x A (y, z)).
It seems like this can be understood that we have a set a which includes all the terms we will be dealing with. Within this set we have a set x, which contains those terms z that result from the functional relation A(y, z). But probably I misread it.]
Axiom P2:
Axiom of Existence of Power Sets
The power set is the collection of all subsets of a set. Historically, in naïve set theory, the PUC was thought to be needed in order to define for any set m, this object, the power set, marked with the curly P [typed here in boldface], P(m), and traditionally and inconsistently, using the PUC to collect all the subsets of m.
P(m) := {y | y⊆m}
But we lack the restriction, so we are not going to do it this way. There is no other way to postulate that the power set exists.
[1.26.10]
Instead:
Axiom on Existence of Power Sets
Let m be a set. There exists a set denoted P(m) whose elements are precisely the subsets of m.
[1.27.00]
Ex: Let m be the set with elements a, b, which themselves are sets. Then the set, the power set of m, is the collection of all subsets. The empty set is an element. Then there are the one-elements subsets. Then there is the entire set. These are all the subsets of m. And they are all collected in the power set of m. More symbolically:
m = {a, b}
P(m) = {∅, {a}, {b}, {a, b}}
[1.28.00]
Is the result is a set? To say it is, we need an extra axiom dedicated to the existence of power sets [for various reasons the others do not work. See 1.28.10].
[We will try to make a formula for the axiom on the existence of power sets. Wikipedia writes this:
In the formal language of Zermelo-Fraenkel axioms, the axiom reads:
∀A ∃P ∀B [B ∈ P ↔ ∀C (C ∈ B → C ∈ A)]
where P stands for the Power set of A,
. In English, this says: Given any set A, there is a set
such that, given any set B, B is a member of
if and only if every element of B is also an element of A. More succinctly: for every set
, there is a set
consisting precisely of the subsets of
.
(Wiki)
So using Schuller’s sort of notation, this might be something like:
∀x ∃p ∀y : (y ∈ p ↔ ∀z (z∈y → z∈x))
It seems here that the original set whose power set we are finding is set x. And set x has members z. When we turn members z into the power set members, by making each one a set in itself and by combing these members z into grouped sets, they then make sets y, which are the members of the power set p. Let us use his example again:
m = {a, b}
P(m) = {∅, {a}, {b}, {a, b}}
And let us compare it to the formulation. Perhaps it is like the following. Here, set m is like set x in the formulation. It is the original set whose power set we are finding. Then, its members a, b are like the z items in the formula. They themselves as individuals can be made into sets, and they can be grouped into other sets. All these possible settings are the terms ∅, {a}, {b}, {a, b}, which are the y terms in the formula. Then, the set of all these y terms is the power set p, which in this example, is {∅, {a}, {b}, {a, b}}.]
Axiom I:
Axiom of Infinity
There exists a set that contains the empty set and with every of its elements y it also contains the set with the element y (or {y}) as an element.
[1.30.40]
Remark: One such set is, informally speaking, the set with the elements, empty set, the set with the element empty set, and with that, the set that contains as an element the set with the empty set as an element, as so on.
∅, {∅}, {{∅}}, {{{∅}}}, ...
We then assign the natural numbers for each of these in the series. There are other sets that are guaranteed by the axiom of infinity, but this is one of those sets.
Corollary: The set of non-negative integers, ℕ, is a set, according to axiomatic set theory.
Remark: As a set, the real numbers, ℝ, can be understood as the power set of the integers.
As a set, ℝ = P(ℕ)
If you take the power set of the reals, and you get a bigger set, and so on until getting to the universe of sets.
[1.34.10]
So the only set we explicitly demanded was the empty set, and on its basis we arrived at the reals.
[Let us try to formulate it. This is from the wiki page:
In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:
∃I (∅ ∈ I ∧ ∀x ∈ I ((x∪{x}) ∈ I)).
In words, there is a set I (the set which is postulated to be infinite), such that the empty set is in I and such that whenever any x is a member of I, the set formed by taking the union of x with its singleton {x} is also a member of I. Such a set is sometimes called an inductive set.
(wiki)
Let us rewrite it more in lines with Schuller’s notations.
∃m (∅∈m ∧ ∀x ∈ m ((x∪{x}) ∈ m)).
So here we have an infinite set m. It contains the empty set. And, for any member of m (perhaps the empty set included), the union of that member with the set containing that member is also in m. But this then becomes a member x, for which the same procedure applies, and this creates another member, which is a set containing a set containing a set, and so on infinitely.]
In total, it will turn out, once all the axioms are there, that essentially every set that we will ever consider in standard mathematics, at least in mathematics built on these axioms, will be ultimately, basically constructed from only the empty set by these construction axioms we wrote down. So set theory is very simple: it is just the empty set. (Schuller 1.35.30)
[Although it is one video lecture, the class itself ends there and the video cuts to the next class where the axiom discussion resumes.]
Axiom C:
Axiom of Choice
Let x be a set whose elements are non-empty and mutually disjoint (that means if you take the intersection of any two elements of the set x, then this intersection will be the empty set), then there exists a set y which contains exactly one element of each element of x.
[1.38.20]
So intuitively speaking, you look at the elements of x, which are all sets, and from each of these sets you pick one element, and you collect them all into the set y. And the axiom of choice guarantees you that there exists such a set that contains exactly one element of each element of x.
Remark: Sometimes people call set y a dark set. Given any set x, there is no clear prescription how you pick an element of each of the elements of x.
Intuition. If you said x consists of pairs of shoes...
x = {{left shoe 1, right shoe 1}, {left shoe 2, right shoe 2}, ... }
You can have an algorithm: always pick the left shoe.
y = {left shoe 1, left shoe 2, ...}
And for this, you do not need the axiom of choice.
[1.40.30]
But if instead you were to consider a set of socks:
x = {{sock 1 (left), sock 1 (right)}, {sock 2 (left), sock 2 (right)} ... }
Note that left and right only tell us they are in a pair. They are indistinguishable as to which is which. So we cannot apply an algorithm like before. We need instead appeal to the axiom of choice to build set y.
y= {sock 1, sock 2, ...}
[1.41.50]
Remark: The axiom of choice is independent of the other 8 axioms. That means we could have set theory with or without the axiom of choice. But standard mathematics uses it.
Remark: There are a number of theorems that can only be proven with the axiom of choice; for example, the proof that every vector space has a basis needs the Axiom of Choice, and the proof that there exists a complete system of representatives of an equivalence relation also requires this axiom.
[1.44.50]
[At this point we should try to create a formulation for the axiom of choice. This is from William Weiss’ An Introduction to Set Theory:
The Axiom of Choice
∀X ((∀x ∈ X ∀y ∈ X (x=y ↔ x∩y ≠ ∅)) → ∃z (∀x ∈ X ∃!y y∈ x∩z))
In human language, the Axiom of Choice says that if you have a collection X of pairwise disjoint non-empty sets, then you get a set z which contains one element from each set in the collection.
(Weiss 28)
So let us look at this formulation. We primarily have an implication. We begin by thinking of a set X. It has members x, y, and z. Let us skip to the end. Here we are speaking of a set z. In the intersection of these sets x and z is a unique y. So the intersection of sets x and z is a set y with just one member. Or perhaps we should say, their intersections are just sets y. In other words, whenever you intersect a set x with a set z, you get a set y, but there can be many such intersections and many such y’s.
So let us think of the socks example.
X = {{sock 1 (left), sock 1 (right)}, {sock 2 (left), sock 2 (right)} ... }
The axiom of choice allowed us to produce from this the following set:
z = {sock 1, sock 2, ...}
So as we can see, the X set is the one that contains a number of other sets, each having sock pairings. I think that the sets x would be the sets {sock 1 (left), sock 1 (right)}, {sock 2 (left), sock 2 (right)}, and so on, and they are contained in the larger set X, which is why there are also the extra braces around all these sets of pairs. The unique y’s, then, would be the members of set z, like sock 1, sock 2, and so on. So what is the intersection of sets x and sets z? Let us compare them:
x are {sock 1 (left), sock 1 (right)}, {sock 2 (left), sock 2 (right)}, and so on.
z is {sock 1, sock 2, ...}
When we intersect them, we just have the members of z. And we see that each member of this intersection is a unique member y from each x set pairing.
The other side of the implication is harder for me to interpret.
∀X ((∀x ∈ X ∀y ∈ X (x=y ↔ x∩y ≠ ∅)) → ∃z (∀x ∈ X ∃!y y∈ x∩z))
Now I am confused, even with Weiss’s explanation. I do not understand why we are considering x and y being equal. I can imagine z and y being equal. But x I would think has more contents than y. Weiss says that “if you have a collection X of pairwise disjoint non-empty sets ...”. I cannot discern how the antecedent of the formulation can be interpreted as saying this. Probably it is because my interpretation of the consequent is wrong, and probably I am mistaken for other reasons too. But apparently what he says is how we are really supposed to read it. It could also be that the x and y are like the two members of each pairing mentioned above. But then I do not understand this part from the consequent, ∃!y y∈ x∩z. If x and y were the two members of each pairing, then if you intersect the x parts of the pairings with the final selection set of z, I would think that you would not have any y’s in it (assuming the x’s and the y’s are thought as different). So I have failed to interpret this formula, and I invite assistance. The intuitive explanation Schuller gives, however, is obvious.]
Axiom F:
Axiom of Foundation
Every non-empty set x contains an element y that has none of its elements in common with x.
It is a non-existence axiom. It excludes certain situations.
Immediate implication: There is no set that contains itself as an element: x∈x for no set x.
[1.48.45]
If you do not have this, then every set needs to be built from the empty set (see axiom of infinity).
[Let us find a formula for the axiom of foundation. Wolfram has it as:
x≠∅ →∃y (y∈x ∧ y∩x = ∅)
More descriptively, “every nonempty set is disjunct from one of its elements.”
(Wolfram)
So in the formula, we begin by considering set x. If set x is a nonempty set, then other things follow. What follows is that it will have a member that when intersecting with x will produce a nonempty set. In other words, set x will have at least one subset whose members are not the same as the members of x. It seems this means that the set x does not include itself as a set. I am not sure, but perhaps this also implies the following. Say we have the set specified as {1, 2}. Perhaps according to this axiom, the set cannot also at the same time be specified both as {1, 2} and {1, 2, {1, 2}}, but I am not sure.]
Images, Ideas, Quotes from:
Frederic P. Schuller. Class Video Lectures 1 and 2 [Taken apparently from actual classes 1, 2, and 3]. “Logic of Propositions and Predicates” and “Axioms of Set Theory.” From his course, “Geometric Anatomy of Theoretical Physics / Geometrische Anatomie der Theoretischen Physik” at the Institute for Quantum Gravity of the University of Erlangen-Nürnberg. Available at youtube at:
Class 1: “Logic of Propositions and Predicates”
https://youtu.be/aEJpQ3d1ltA
Class 2: “Axioms of Set Theory”
https://youtu.be/Cw5GkdgLgPo
Course Lecture Playlist on Youtube:
https://www.youtube.com/playlist? list=PLPH7f_7ZlzxTi6kS4vCmv4ZKm9u8g5yic
And Schuller’s page:
https://www.gravity.physik.fau.de/members /people/schuller.shtml
Or if otherwise indicated:
Weiss, Willaim A. R. An Introduction to Set Theory. [Class notes soon to be published as a book]
<http://www.math.toronto.edu/weiss/set_theory.pdf
Michael Rieppel’s online truth table generator
http://mrieppel.net/prog/truthtable.html
James Aspnes mathematical logic wiki:
http://www.cs.yale.edu/homes/aspnes/p inewiki/MathematicalLogic.html
Wiki pages:
https://en.wikipedia.org/wiki/Axiom_of_power_set
https://en.wikipedia.org/wiki/Axiom_of_infinity
https://en.wikipedia.org/wiki/Axiom_of_pairing
Wolfram pages:
http://mathworld.wolfram.com/Zermelo- FraenkelAxioms.html
http://mathworld.wolfram.com/AxiomofChoice.html
http://mathworld.wolfram.com/AxiomofFoundation.html</ a>
.







































































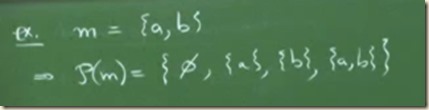







I'd love to borrow/refer to this from my blog because it helps flesh out some of the work I've been doing.
ReplyDeleteThanks! I am not a logician, and I did this before doing a lot of other logic work on the blog. So I would not recommend trusting my summaries over the original lecture material itself. I tried to follow the lecture as closely and faithfully as I could, but I doubt my explanations are adequate. Instead I think it is best to just use Schuller's lecture itself. But if you would like to save time taking screenshots or writing out formulas or whatever else, you can use what I have here. Just please let me know what your own blog is so I can check it out! -Corry
Delete