summary by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Entry Directory for this Article]
[The following is summary. My own comments and citations are placed in double brackets. All boldface and underlying are mine.]
Mikhail G. Katz and David Sherry
“Leibniz’s Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond”
4. Cum Prodiisset
4.5 Mathematical Implementation of Status Transitus
Brief Summary:
In Cum Prodiisset Leibniz discusses his Law of Continuity, and he provides some examples. Katz and Sherry will examine some of the mathematical procedures involved in these examples. What we find is that the same formulations and procedures are used regardless of whether we are dealing with finite or infinite values. This is because the law of continuity postulates that what holds for the finite holds for the infinite (and infinitesimal), [because there is a continuous transition from one to the other.]
Summary
In section 4.2 and 4.4, Katz and Sherry (KS) discuss three applications of Leibniz’ law of continuity and infinitesimals in his Cum Prodiisset. Now they will examine them more mathematically.
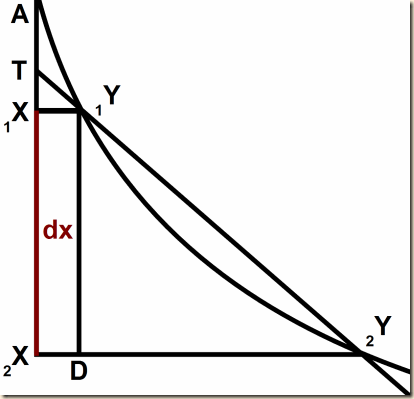
Leibniz distinguishes assignable finite quantity d(x) from infinitesimal value dx.
The assignable quantity (d)x passes via infinitesimal dx on its way to absolute 0. Then the infinitesimal dx is the terminus, or the status transitus. Zero is merely the shadow of the infinitesimal. This particular status transitus is the foundation rock of the Leibnizian definition of the differential quotient.
[KS 581]
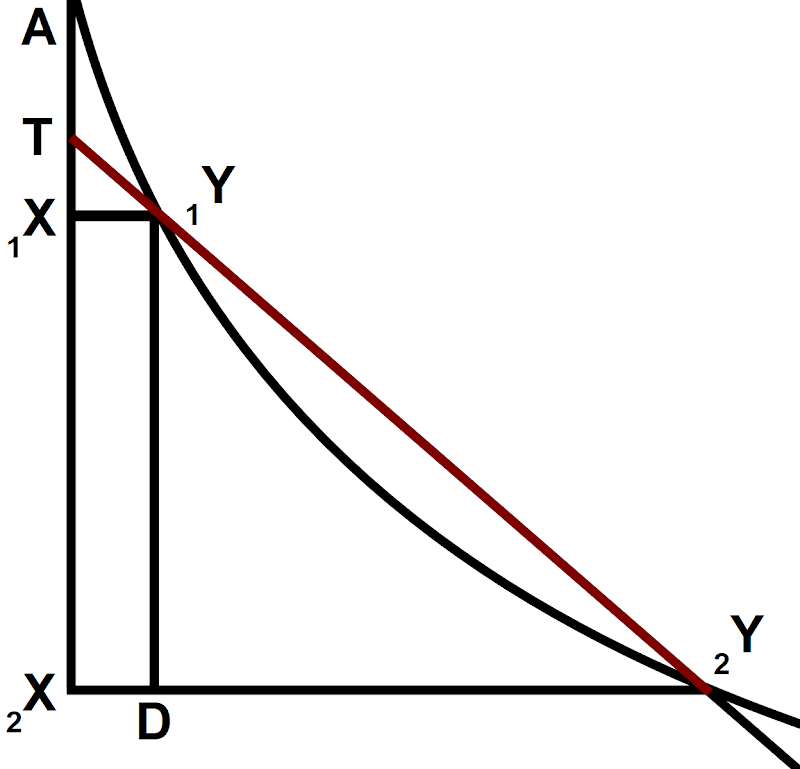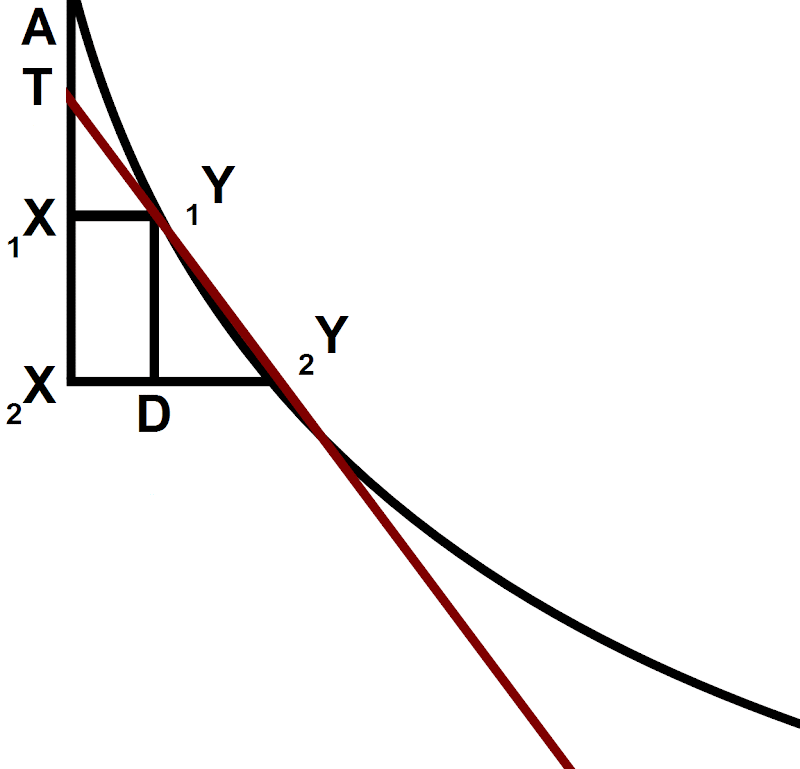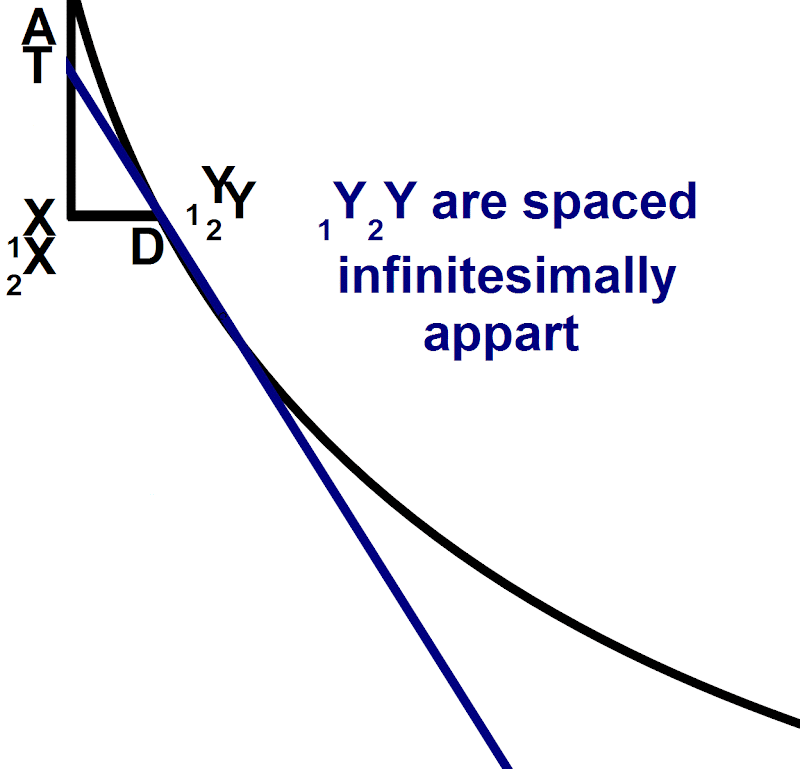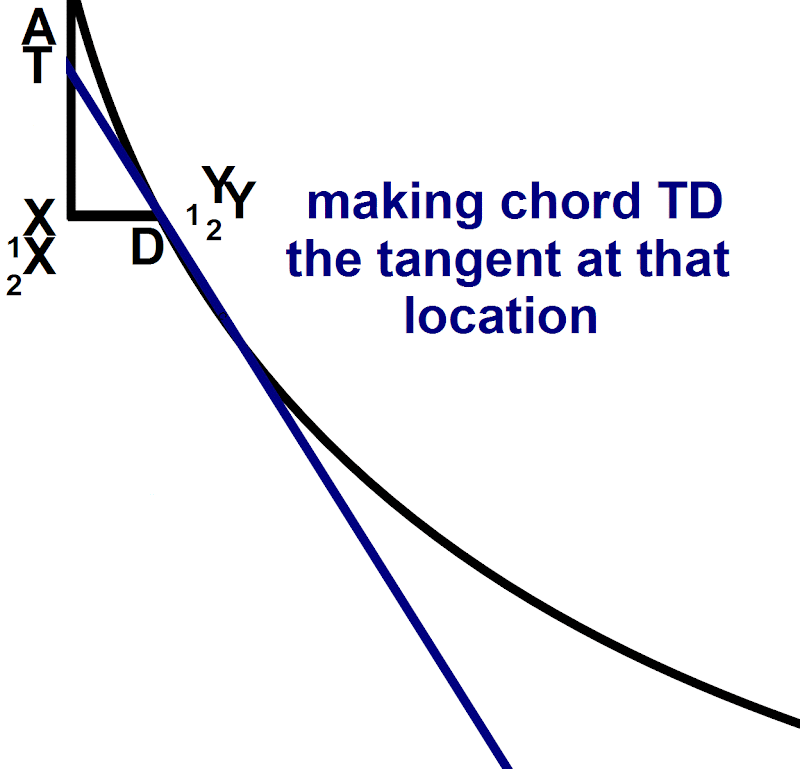
[Recall Leibniz’ example of finding the tangent to a parabola. He writes:
“let 1X2X, the difference between A1X and A2X, be called dx;”
“and similarly, let D2Y, the difference between 1X1Y and 2X2Y, be called dy.” (Leibniz 151)
Then, we shrink dx and dy down to find the tangent.
(Animated diagram by Corry Shores, using OpenOffice Draw and Unfreez)
Here Leibniz does not notate a difference between dx and d(x), but we would think of the finitely large line as being d(x) and the infinitesimally small one as dx.
KS also refer to Z as being the shadow of the infinitesimal. In the appendix they explain the shadow as being a real number assigned to hyperreal infinitesimals. It is the next closest value, only infinitesimally different. In these cases below, the shadow is like rounding the infinitesimal value to the nearest real number.]]
Let’s recall the first example Katz and Sherry examine:
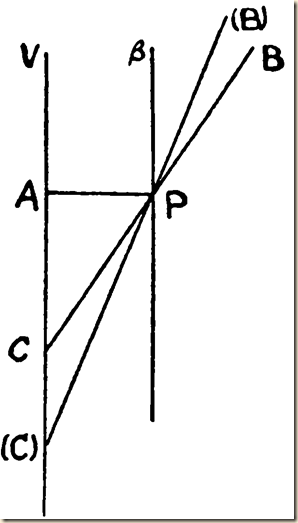
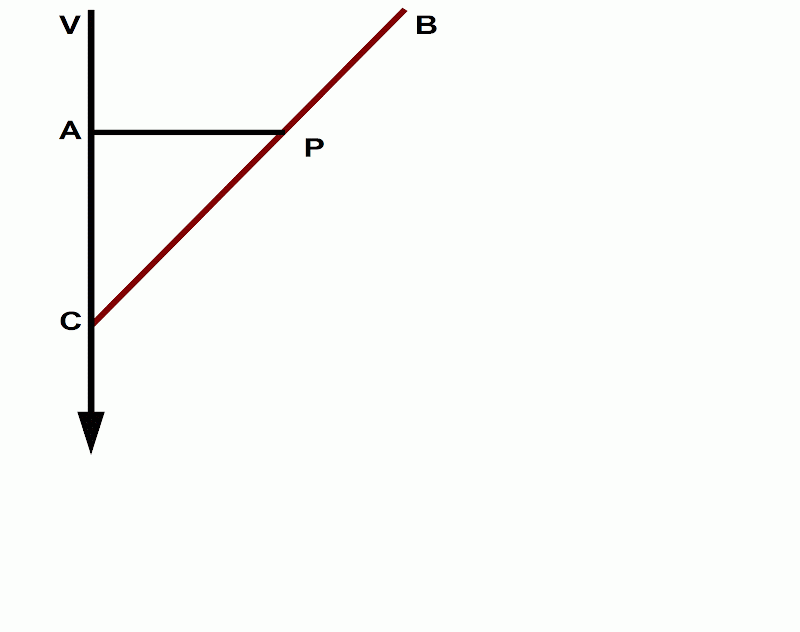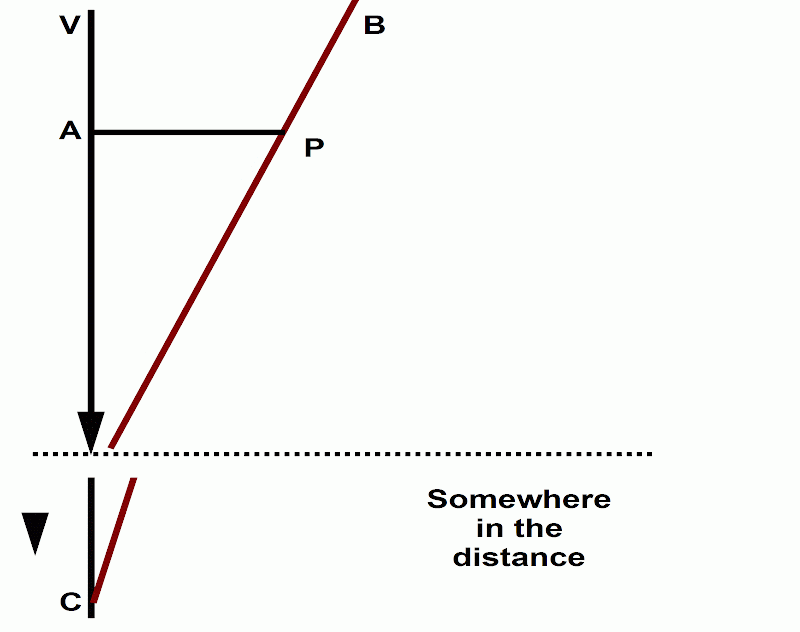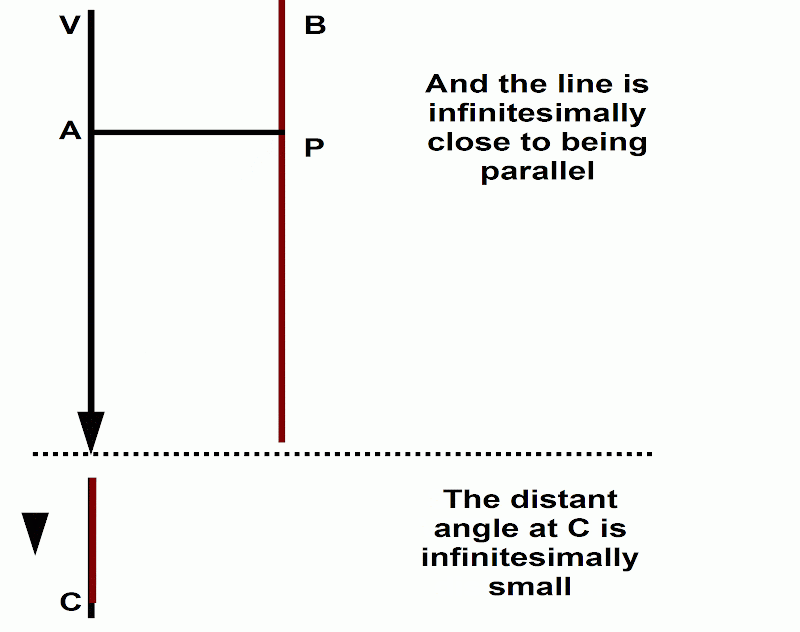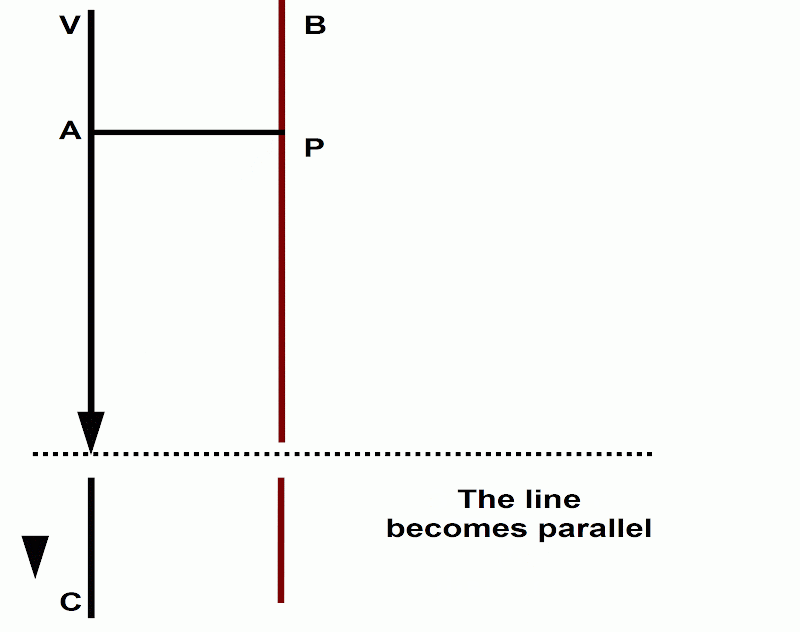
(1) In the context of a discussion of parallel lines, he writes: when the straight line BP ultimately becomes parallel to the straight line VA, even then it converges toward it or makes an angle with it, only that the angle is then infinitely small (Child 1920, p. 148).
[[KS579]]
[Image from Leibniz/Child 148]
[We animated it thus:
(Animated diagram by Corry Shores, using OpenOffice Draw and Unfreez)
]
In KS’s rendition, they have us think of this diagram on its side with the moving line intercepting the x axis. In their formulation, H is the x-intercept value.
Example (1) of parallel lines can be elaborated as follows. Let’s follow Leibniz in building the line through the point (0,1) parallel to the x-axis in the plane. Line LH with y-intercept 1 and x-intercept H is given by y = x / H .
[KS 581]
[Referring back to Leibniz’ diagram, the y-intercept here is like point P, which remains the same, all while the x-intercept, equivalent to point C, moves to greater distances.]
We will move the x-intercept to infinity. [KS later refer to the ‘finite portion of LH.’ Perhaps one way to picture this is to think that the lines meet way off into infinity, but they ‘drag’ the finite part of the line all the way up such that it is only infinitesimally away from being y = 1. Yet, somewhere the lines must meet, which means it cannot stay at y = 1 everywhere. So does that mean that in the infinite part, it is no longer infinitely close to being parallel? I am not sure, but I think it is always infinitely close to being parallel, but just not always being infinitely close to y = 1. So far off into infinity, it will maybe be infinitely close to being parallel to y = 0.5, and so on diminishing. For every y position of the line in its infinite part, there would be an infinite stretch both ways, making every position be nearly parallel to the line.]
Now let H be infinite. The resulting line LH has negative infinitesimal slope, meets the x-axis at an infinite point, and forms an infinitesimal angle with the x-axis at the point where they meet. We will denote by st(x) the assignable (i.e., real) shadow of a finite x. [KS 581]
[They now will formulate for finite values for the x and y locations included in Line H.]
Then every finite point (x,y) ∈ LH satisfies
[by substituting the formula for y. Now, because we are supposing H to be infinite, that means you have a finite value divided by an infinite one, which means it is nearly zero, which means that the y value is very close to 1, and thus:]
Hence the finite portion of LH is infinitely close to the line y = 1. The line y = 1 is parallel to the x-axis, and is merely the shadow of the inassignable LH. Thus, the parallel line is constructed by varying the oblique line depending on a parameter. Such variation comprises the status transitus LH defined by an infinite value of H.
[KS 582]
Now recall example 3:
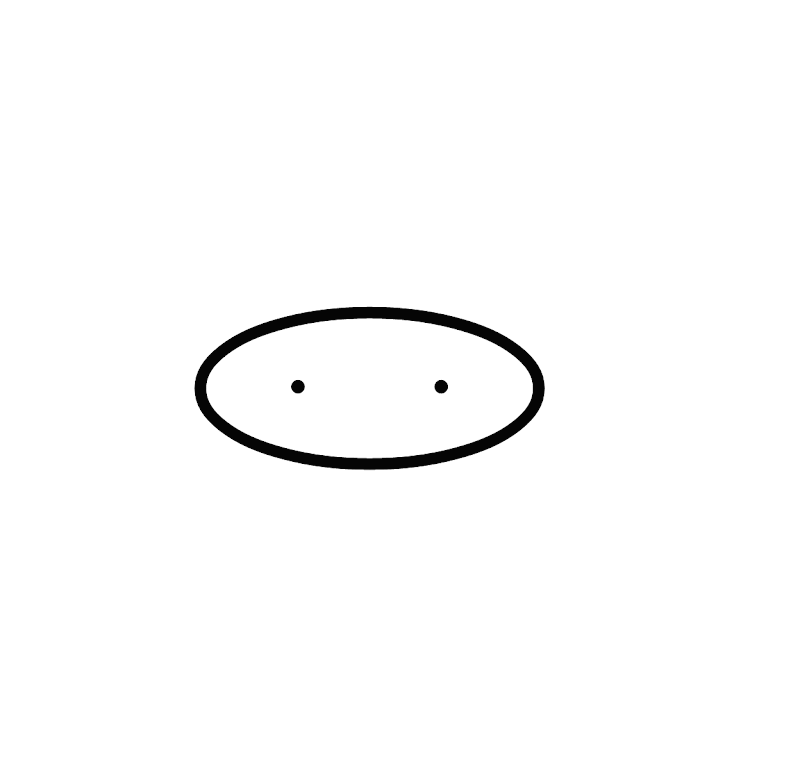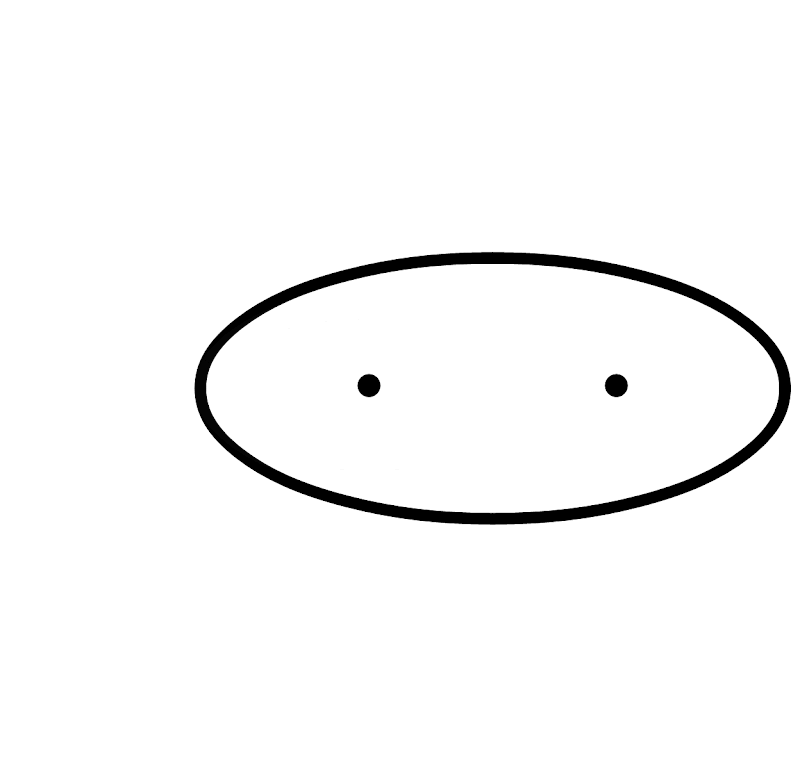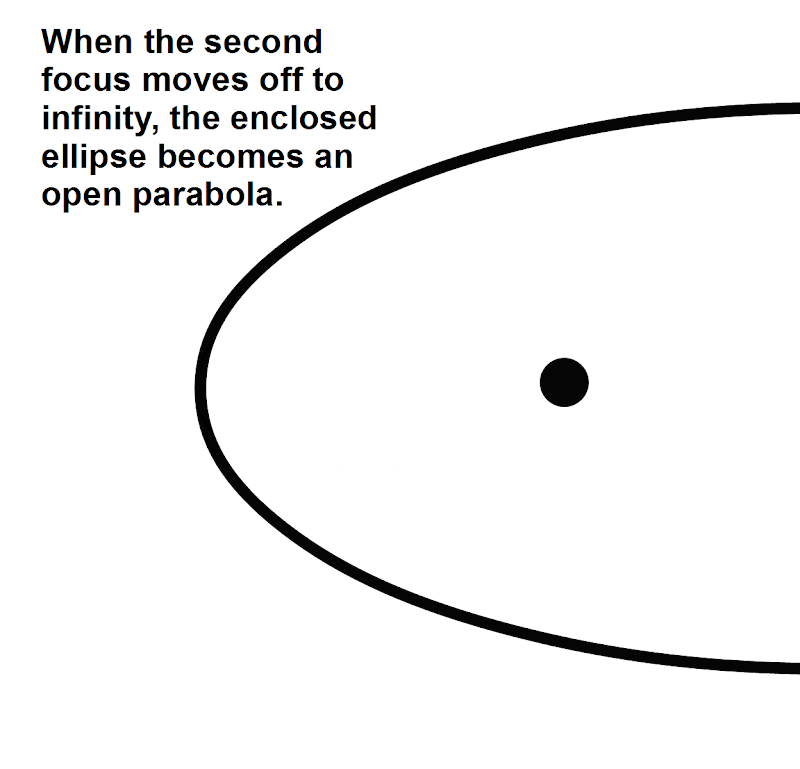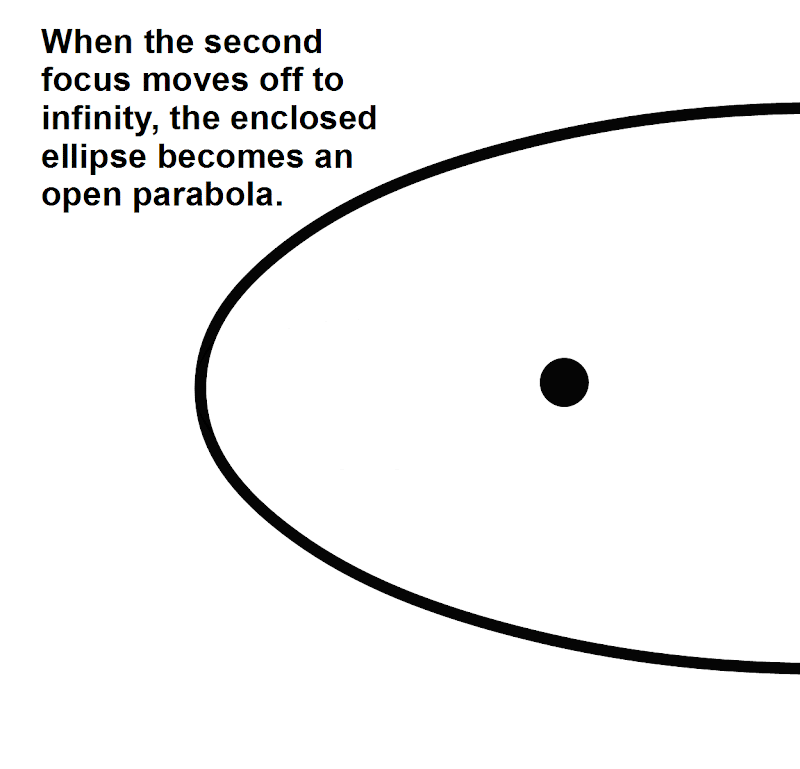
(3) Finally, a conception of a parabola expressed by means of an ellipse with an infinitely removed focal point is articulated in the following terms: a parabola is the ultimate form of an ellipse, in which the second focus is at an infinite distance from the given focus nearest to the given vertex (Child 1920, p. 148).
[KS 579]
[[Recall from our prior discussion that by moving one focus of the ellipse infinitely away from the other, the ellipse transforms into a parabola.
(Animated diagram by Corry Shores, using OpenOffice Draw and Unfreez)
]
KS will provide a formulation to illustrate this better.
To implement example (3), let’s follow Leibniz in deforming an ellipse, via a status transitus, into a parabola. The ellipse with vertex (apex) at (0,-1) and with foci at the origin and at (0,H) is given by
[They then square both sides and expand the values:]
Then they kept the radical on the left side, moving the rest over:
Then they square both sides, and reduce to get:
[We notice that even though H is an infinite number, they still apply operations on the figures that normally apply to finite numbers. But whether or not that is mathematically admissible is uncertain, hence it the ‘postulate’ of the law of continuity that we can treat them in like manner.]
The calculation (4.1) through (4.4) depends on the following habits of general reasoning (to echo Child’s translation) with assignable quantities, which are generalized to apply to inassignable quantities (such as the terminus/status transitus) in accordance with the law of continuity:
• squaring undoes a radical;
• the binomial formula;
• terms in an equation can be transferred to the other side; etc.
General reasoning of this type is familiar in the realm of ordinary finite real numbers, but why does it remain valid when applied to the realm of infinite or infinitesimal numbers? The validity of transfering such general reasoning originally instituted in the finite realm, to the realm of the infinite is postulated by Leibniz’s law of continuity.
[KS 582]
[Because the same general reasoning is used for finite and infinite, that might give a ‘between’ status or ambiguous status to the status transitus. Notice that we are still using a formulation for an ellipse. And yet, the resulting figure is in transit to being a parabola. Off in infinity, it might be still elliptical. But it draws out the finite part such that only parabolic parts remain within the realm of assignable values.]
We therefore apply Leibniz’s law of continuity to Eq. (4.4) for an infinite H. The resulting entity is still an ellipse of sorts, to the extent that it satisfies all of the Eqs. (4.1) to (4.4). However, this entity is no longer finite. It represents a Leibnizian status transitus between ellipse and parabola. This status transitus has foci at the | origin and at an infinitely distant point (0, H).
[KS 582|583, boldface mine]
[[Recall that we left off before with:
It seems in the following that KS will assign real numbers so to find the “real shadow” of this figure, that is, the finite assignable values it is infinitely close to.]]
Assuming x and y are finite, we set x0 = st(x) and y0 = st(y), to obtain a real shadow of this entity:
then simplifying:
Thus, the finite portion of the status transitus (4.4) is infinitely close to its shadow (4.5), namely the real parabola y ¼ x2 4 1 (in Leibniz’s terminology as translated by Child, ‘‘it is really true’’ that this parabola has no focus at infinity—see Sect. 4.4). This is the kind of payoff Leibniz is seeking with his law of continuity.
[KS 583]
Bibliography:
Katz, M.; Sherry, D. Leibniz's Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond. Erkenntnis 78 (2013), no. 3, 571-625. See http://dx.doi.org/10.1007/s10670-012-9370-y, http://www.ams.org/mathscinet-getitem?mr=3053644, and http://arxiv.org/abs/1205.0174
The above bibliography material taken from the following source, a page by Mikhail Katz, which links to many other recent publications on infinitesimals.











































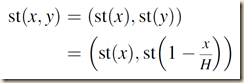
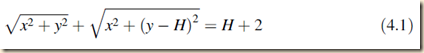
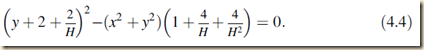
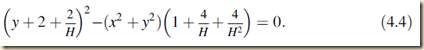

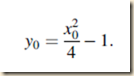
No comments:
Post a Comment