summary by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Entry Directory for this Article]
Mikhail G. Katz and David Sherry
“Leibniz’s Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond”
1. Introduction
Brief Summary:
Many calculus historians deny a historical continuity from Leibniz’ concept of infinitesimals to Robinson’s. Part of the reasoning behind their conclusion is that Berkeley successfully proved the flaws of this concept, and Robinson built his notion of the infinitesimal using modern logical tools that were unavailable to Leibniz. The authors will show that Berkeley’s critique does not hold so strongly, because Leibniz’s infinitesimal is rigorous even to today’s standards, and thus there may in fact be a historical continuity from Leibniz to Robinson.
Summary
The calculus Leibniz invented was based on infinitesimal (infinitely small) quantities. This concept of the infinitesimal was seen as being not mathematically rigorous. However, in the 20th century, Abraham Robinson invented non-standard analysis, which provides a consistent theory of infinitesimals. But since Robinson’s non-standard analysis makes use of modern logic, many commentators say that there is no historical continuity from Leibniz’ to Robinson’s infinitesimals. (572)
Robinson himself suggests a link to Leibniz via Hilbert, as all three regard infinitesimals as not real entities. (572) For Leibniz, infinitesimals are mental fictions. Nonetheless, this does not prevent them from being meaningful:
Leibniz’s was a remarkably modern insight that mathematical expressions need not have a referent, empirical or otherwise, in order to be meaningful. (Katz and Sherry [henceforth KS, or ‘the authors’] 572)
KS will argue primarily two things.
1) “Leibniz’ system for the calculus was free of contradiction, and incorporated versatile heuristic principles such as the law of continuity and the transcendental law of homogeneity” [see Fig 1, reproduced below] (572d). And
2) they will “undermine the view that Berkeley’s objections to the | infinitesimal calculus were so decisive that an entirely different approach to infinitesimals was required.” (572|573)
Jesseph (in his Berkeley’s philosophy of mathematics. Science and its Conceptual Foundations) argues that this early concept of the infinitesimal was “a conceptual dead-end, and a consistent theory of infinitesimals required a fresh start.” (KS 573) The authors, however, will argue that “Leibniz’s defense of the infinitesimal calculus—both philosophical and mathematical—guided his successors toward an infinitesimal analysis that is rigorous by today’s standards.” (573) To do this, they will show that Berkeley’s critiques “stem from philosophical presuppositions which are neither necessary nor desirable from Leibniz’s perspective.” (573)
Bibliography:
Katz, M.; Sherry, D. Leibniz's Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond. Erkenntnis 78 (2013), no. 3, 571-625. See http://dx.doi.org/10.1007/s10670-012-9370-y, http://www.ams.org/mathscinet-getitem?mr=3053644, and http://arxiv.org/abs/1205.0174
The above bibliography material taken from the following source, a page by Mikhail Katz, which links to many other recent publications on infinitesimals.










































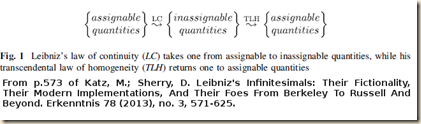
No comments:
Post a Comment