by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Mathematics, Calculus, Geometry, Entry Directory]
[“On the Equilibrium of Planes”, Entry Directory]
Archimedes
On the Equilibrium of Planes
or
The Centres of Gravity of Planes,
Book I
Proposition 12
[The following is quotation]
Proposition 12
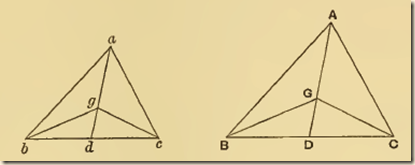
P12. Given two similar triangles abc, ABC, and d, D the middle points of bc, BC respectively, then, if the centre of gravity of abc lie on ad, that of ABC will lie on AD.
Let g be the point on ad which is the centre of gravity of abc.
ad : ag = AD : AG,
and join gb, gc, GB, GC.
Then, since the triangles are similar, and bd, BD are the halves of bc, BC respectively,
ab : bd = AB : BD,
and the angles abd, ABD are equal.
Therefore the triangles abd, ABD are similar, and
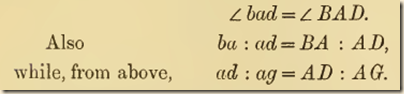
Therefore ba : ag = BA : AG, while the angles bag, BAG are equal.
Hence the triangles bag, BAG are similar, and
And, since the angles abd, ABD are equal, it follows that
In exactly the same manner we prove that
(Heath 197)
Therefore g, G are similarly situated with respect to the
triangles respectively; whence [Prop. 11] G is the centre of
gravity of ABC.
(Heath 198)
From:
Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at
https://archive.org/details/worksofarchimede00arch











































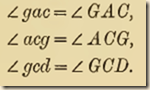
No comments:
Post a Comment