Archimedes’ “On the Equilibrium of Planes”, Prop 11

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

 

[Central Entry Directory]

[Mathematics, Calculus, Geometry, Entry Directory]

[Archimedes Entry Directory]

[“On the Equilibrium of Planes”, Entry Directory]

 

Archimedes

On the Equilibrium of Planes

or

The Centres of Gravity of Planes,

Book I

Proposition 11

[The following is quotation]

 

Proposition 11

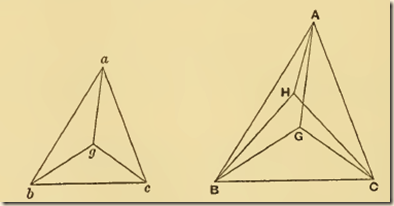
P11. If abc, ABC he two similar triangles, and g, G two points in them similarly situated with respect to them respectively, then, if g be the centre of gravity of the triangle abc, G must be the centre of gravity of the triangle ABC.

Suppose ab : bc : ca = AB : BC : CA.

The proposition is proved by an obvious reductio ad absurdum. For, if G be not the centre of gravity of the triangle ABC, suppose H to be its centre of gravity.

Post. 5 requires that g, H shall be similarly situated with respect to the triangles respectively; and this leads at once to the absurdity that the angles HAB, GAB are equal.

(Heath 196)

 

From:

Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at

https://archive.org/details/worksofarchimede00arch