by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[John Nolt, entry directory]
[Nolt, Logics, entry directory]
[The following is summary. All boldface in quotations are in the original unless otherwise noted. Bracketed commentary is my own. As proofreading is incomplete, you will find typos and other districting errors. I apologize in advance.]
Summary of
John Nolt
Logics
Part 5: Nonclassical Logics
Chapter 15: Mildly Nonclassical Logics
15.2 Multivalued Logics
Brief summary:
There are a number of reasons to be dissatisfied with the bivalence of classical logic, that is, with the limitation to just two values, true (T) and false (F). Among these reasons are: 1) some sentences are unintelligible and would thus seem to be neither T nor F, 2) some sentences have terms that fail to refer to an object, which might make us want to say they are neither T nor F, 3) semantic paradoxes, such as the liar’s paradox, would seem to have neither a T nor a F value, 4) there are metaphysical issues that could compel us to consider certain situations as being neither T nor F, as for example when making statements now about an unknowable future, 5) certain practical concerns, as for example in computer database creation, where designating certain formulas as neither T nor F is more useful, and 6) the vagueness of situations can make clear-cut propositions about their real status difficult on account of ambiguities, and hence we would not want such statements to be entirely T or F. Thus we have cause for devising logics with three or more values. Three such multivalued semantics are Bochvar’s, Kleene’s, and Łukasiewicz’s. In all three, a third value, namely indeterminate or ‘I’, is added, but how propositions containing indeterminate values are evaluated varies in each system.
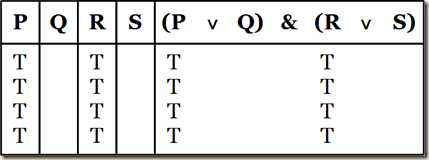
Truth Tables for Bochvar’s Three-Valued Semantics

(Nolt 408)
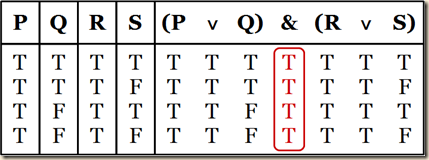
Truth Tables for Kleene’s Three-Valued Semantics
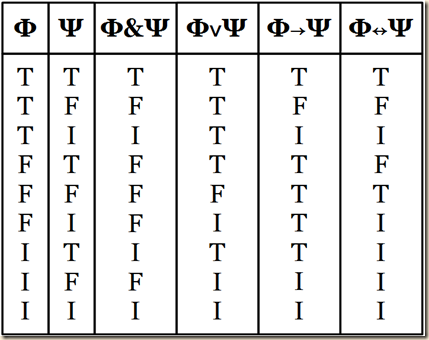
(Nolt 412)
Truth Tables for Łukasiewicz’s Three-Valued Semantics

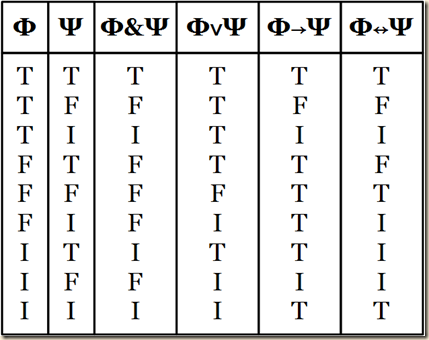
(Nolt 413)
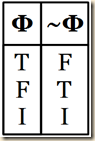
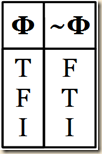
Each will make certain classical tautologies valid or invalid, depending on how they evaluate in each semantic. And each one in some way may make certain counter-intuitive tautologies in classical logic become invalid, and certain intuitive classical tautologies become invalid. In each semantics, an operator for ‘it is true that’, symbolized T, may be used for establishing tautologies, since it converts values to just T or F. (Without this operator, classical tautologies in these three-valued semantics can be valued as indeterminate. Thus not all valuations would make it true, and hence they would no longer be tautologous). Its truth table is the following:

(Nolt 411)
Summary
So far in this book (and as announced in section 3.1), we have only considered the two truth values, T and F, and we also assumed “that each statement had exactly one of these truth values in every possible situation” (Nolt 406). Nolt now says that “there are reasons not to be satisfied with it” (406). He gives as one sort of case grammatically well formed sentences that “seem to have no intelligible meaning” (406). He offers as an example, “Development digests incredulity” (406). It is not clear what it means. Suppose we simply conclude that it is false. But that means “Development does not digest incredulity” would have to be true. But since it is not more intelligible that the non-negated form, we seem to have the same reason to say that it also should be false. [Nolt’s next ideas seem to be the following. Since the sentences unintelligibility makes it impossible to determine its truth value, we can say that it is a sentence but also that it is one whose value is neither true nor false. Or, we can go further and say that it is not even a sentence and thus truth and falsity (or its lack of them both) is not even a relevant issue. Let me quote:]
We might, then, decide to rule them both out of court; they both, we might conclude, are neither true nor false. Against this conclusion, some have objected that since neither sentence is really intelligible, neither makes a statement, and where no statement is made there is nothing that can be either true or false. The question of truth or falsity simply does not arise. On this view, unintelligible sentences do not challenge the principle of bivalence because that principle applies only to statements.
(406)
[So one situation where bivalence is problematic is with sentences that are unintelligible.] Another situation where bivalence is problematic are cases of reference failure [where the sentence is intelligible but also where certain terms in it do not refer to something, and thus the conditions for determining its truth value are lacking] (Nolt 406). Nolt offers as an example the following sentence: “The Easter Bunny is not a vegetarian”. We might be inclined to deem the sentence as not true, because the Easter Bunny does not exist (406). If we deem it not true, then we would conclude it is false, in a bivalent system. [So now, “The Easter Bunny is a vegetarian” is false, and thus in a bivalent system, “The Easter Bunny is a not a vegetarian” would be true.] But then, Nolt asks, would it be true that the Easter Bunny is a carnivore? As we can see, when a subject that is being predicated does not refer to some object, it would seem that the sentence can be neither true nor false.
The problem, of course, is that since the term ‘The Easter Bunny’ does not pick out an object of which we may predicate either vegetarianism or nonvegetarianism, it seems misleading to think of these sentences as either true or false. We might reasonably conclude, then, that because of the reference failure they are neither. Notice that here it is less plausible to argue that no statement has been made. We understand perfectly well what it means to say that the Easter Bunny is a vegetarian. But what is asserted seems not to be either true or false.
(406)
Another case that challenges bivalence are the semantic paradoxes, and in fact they present “even stronger arguments against the principle of bivalence” (407). He has us consider a sentence called “S” which says:
Sentence S is false.
(407)
Nolt says that with this sentence,
we can actually offer a metalinguistic proof that it is neither true nor false. For suppose for reductio that it is true. Then what it says (that it is false) is correct, and so it is false. It is, then, on this supposition both true and false, which contradicts the principle of bivalence. Suppose, on the other hand, that it is false. Then, since it says of itself that it is false, it is true. Hence once again it is both true and false, in contradiction to the principle of bivalence. Hence, from the principle of bivalence itself, we derive by reductio both the conclusion that this sentence is not true and the conclusion that it is not false. It is, then, certainly not bivalent.
(407)
[Nolt will now have us consider another sort of logical situation that challenges bivalence. For this, we should first recall the model of time that we discussed in section 13.2.1. Here, time was nondeterministic, but statements about the future could still be true in the present, if in fact they are going to be true in the future. Another view argues that were this so, it is not really an nondeterministic system. To be such, contingent statements about the future should be neither true nor false until their value is determined at the relevant future moment. This view was put forth by Jan Łukasiewicz. Were one to take up this position, one could thus object to bivalence for metaphysical reasons.]
One might also reject bivalence on metaphysical grounds. Jan Łukasiewicz, who constructed the first multivalued semantics early in the twentieth century, held that contingent statements about the future do not become true until made true by events. Suppose, for example, that a year from now you decide to write a novel. Still it is not true now that a year from now you will decide to write a novel; the most that is true now is that it is possible that you will and possible that you won't. Only when you actually do decide a year hence does it become true that a year earlier you were going to decide to write a novel a year hence. Obviously, Łukasiewicz’s conception of time is different from that presented in Section 13.2, where we modeled a nondeterministic time in which contingent statements about the future may be true at present. Łukasiewicz assumed that the present truth of contingent statements about the future implies determinism. In any case, the idea that the truth of a contingent statement does not “happen” until a specific moment in time, whether right or not, is of logical interest. It implies that many statements about the future are neither true nor false now so that there is some third semantic status, which Łukasiewicz called ‘possible’ or ‘indeterminate’, in addition to truth and falsity.
(407, boldface mine)
[The reasons for rejecting bivalence so far are unintelligible sentences, reference failure, semantic paradoxes, and metaphysical issues like the indeterminacy of presently made statements about the unknowable future.] The next reason Nolt gives for rejecting bivalence is that particular statements would for certain practical reasons be best considered as having an unknown truth value in computer databases. [The idea seems to be that the database will function better, or that the programming can be more efficient or effective, were certain statements considered neither true nor false, even if in actual reality they are one of the two.]
There may also be more mundane, practical grounds for rejecting bivalence. The designers of a computer database of propositions, for example, might want to list some propositions as true, some as false, and others as unknown. There is, of course, no metaphysical basis for the third value in this case. The propositions listed as unknown may all in fact be true or false. But in practice the inferential routines used with the database may work best if they embody a non-bivalent logic.
(407)
The final motivation for rejecting bivalence that Nolt offers are cases of vagueness, where truth is perhaps better understood as having different degrees. Nolt gives the example of the sentence “This is a car” in reference to a midsize sedan. This is entirely true. But if we said, “This is a car” in reference to an eighteen-wheeler, then it would be entirely false. Yet, what if we said this in reference to a van?
Many people feel that such assertions are “sort of true, but not exactly true.” Since, like ‘car’, virtually all words are somewhat vague, for virtually all statements there are borderline situations in which we are hesitant to say that the statement is either true or false. But the notion that truth comes in degrees leads beyond consideration of a mere third alternative to truth and falsity into the realm of infinite valued and fuzzy logics ( see Section 16.1).
[So we have the following reasons to consider an alternative to bivalent logic:
1) unintelligible sentences,
2) reference failure,
3) semantic paradoxes,
4) metaphysical issues (like the indeterminacy of presently made statements about the unknowable future)
5) practical concerns (as for example in computer database creation)
6) vagueness
] On account of these issues, we might want to consider that perhaps there exists, or at least that it would be useful to incorporate, a third truth value in addition to truth and falsity (Nolt 408). Nolt for now will posit just one such value, the indeterminate, notated as “I” (Nolt 408). But as we might imagine, we will need to revise our standard truth tables to accommodate the properties of this value. When we assign truth values to sentences, we can now assign T, F, or I. Yet, there is not just one way to assign values. We can at least say that when formulas that are “governed by the operators” and also that have components that are all either true or false, then they will take their usual truth values on the whole (408). But we still need to determine what to do when complex sentences have at least one component with the value I. Nolt says there are two general policies for these cases (408), [namely, that even one internal instance of I should make the whole sentence I, or instead such a sentence (with one instance of I) could have the value T or F, depending on how the semantics is constructed.]
Two general policies suggest themselves:
1. Indeterminacy of the part should infect the whole so that, if a complex formula has an indeterminate component, then the formula as a whole should be indeterminate.
2. If the truth value of the whole is determined on a classical truth table by the truth or falsity of some components, even if other components are indeterminate, then the whole formula should have the value so determined.
(Nolt 408)
Nolt illustrates the difference in how these policies would work by having us consider a disjunction ‘P∨Q’, where ‘P’ has the value T and ‘Q’ has the value I. We now wonder, what is the value of the entire disjunction? The first policy would say that it is I, because part of it is I. However, the second policy would note that even though one term is indeterminate, it still fulfills the requirements for a true disjunction in the classical truth table, because at least one disjunct is true (Nolt 408).
Nolt says it is “not obvious which of these policies is preferable,” and in fact “one may be preferable for some applications, the other for others” (Nolt 408). For this reason, Nolt will discuss both policies, and at the end of the section, he will consider yet a third policy (408).
In line with the first policy, Russian logician D.A. Bochvar, in the late 1930’s “proposed a three-valued semantics for propositional logic” where “the indeterminacy of a part infects the whole” (Nolt 408). Such a semantics is shown in these truth tables [taken from Nolt 408]:


(Nolt 408)
Nolt has us recall how in classical logic where there are only 2 values, there are 2n valuations, which would be 2n horizontal lines in the truth tables, for sentences containing n sentence letters (409). [So the first table above for negation, in a bivalent logic, would only have 2 horizontal rows, and the set of tables below it would have 4]. But since here we have three values, there are 3n valuations, and thus in the second set of tables above, there are 9 rows (409).
Nolt then shows how this additional complexity factors into the valuation rules in Bochvar’s logic. Here Nolt just gives the rules for negation and conjunction.
v(~Φ) = T iff v(Φ) = F
v(~Φ) = F iff v(Φ) = T
v(~Φ) = I iff v(Φ) = I
v(Φ&Ψ) = T iff v(Φ) = T and v(Φ) = T
v(Φ&Ψ) = F iff either v(Φ) = F and v(Ψ) = T, or v(Φ) = T and v(Ψ) = F, or v(Φ) = F and v(Ψ) = F.
v(Φ&Ψ) = I iff either v(Φ) = I or v(Ψ) = I, or both.
(Nolt 409)
Nolt then notes some of the “striking features” of this sort of logic. 1) all classically tautologous formulas are not tautologous in Bochvar’s semantics. We consider for example the tautology ‘P→P’. [Here, whether P is true or false, the formula will be true regardless.] But in Bochvar’s semantics, if P is I, then the formula is I. That means it is no longer true on all evaluations and is thus not tautologous. Nolt adds however that we can at least say of the classical tautologies that in Bochvar’s logic they are never false (Nolt 409).
If we wanted the classical tautologies to remain distinguished as such in Bochvar’s semantics, then we could define a tautology as “any formula which is not false on any line of its truth table – that is, which is either true or indeterminate on all lines” (409). [Nolt introduces a term here, designated. A truth value is designated if it counts towards a formula being tautologous.]
it comes down to a question of which truth values we shall accept as designated – that is, which values count toward tautologousness. If a statement must be true on all lines of its truth table to count as a tautology, then T is the only designated value. If a statement need merely be either true or indeterminate on all valuations, then both T and I are designated values. For Bochvar, only T was designated.
(409, boldface his)
Nolt turns now to the notion of validity, which also involves different options for how to define it. When there are just two values, T and F, then it does not matter which of the following definitions we use, as they will both suffice to identify the valid formulas.
a sequent is valid iff:
1) there is no valuation on which its premises are all true and its conclusion is untrue.
2) there is no valuation on which its premises are all true and its conclusion is false.
(409)
As Nolt explains,
Given bivalence, untruth and falsity are the same thing. In a multivalued logic, however, the difference between the two definitions is substantial, for there may | be valuations on which the premises are true and the conclusion is indeterminate.
(409-410, boldface mine)
[We should here consult Nolt’s definition of counterexample from earlier in the book: “A possible situation in which an argument’s premises are true and its conclusion is not true is called a counterexample to the argument. We may define validity more briefly simply by saying that a valid argument is one without a counterexample” (6, boldface his). Notice the wording of “its conclusion is not true). Thus using this definition, we would have a counterexample if the premises are true and the conclusion is indeterminate.] Nolt asks if we should consider instances where the premises are true and the conclusion indeterminate as counterexamples, and he replies:
If we think so, we will adopt the first definition of validity. If we think not, we will adopt the second. Bochvar adopted the first, and it is the one we shall use here. Indeed, we stipulate now that we shall for the purposes of this section (and particularly the exercise at the end) retain the wording of all the definitions of semantic concepts presented in Chapter 3.
(410)
Nolt then notes how Bochvar’s semantics can invalidate certain sequents “that at least some logicians have regarded as suspect” (410). He offers for example the “paradoxes of material implication” [but he does not explain why one might object to these arguments]:
Q ⊢ P → Q
~P ⊢ P → Q
[Nolt does not make the truth tables, so the ones I provide in the following may be incorrect.


As we can see, there are no horizontal lines where the premise is true but the conclusion not true. Now let us examine these sequents using Bochvar’s semantics.


Here we can see that there is a line in each where the premise is true but the conclusion is not true. Thus in this semantics they are not valid arguments.]
Q ⊢ P → Q
~P ⊢ P → Q
though valid in classical logic, are on Bochvar's semantics invalid. In the first case, the counterexample is the valuation on which ‘Q’ is true and ‘P’ indeterminate, which makes the premise true and the conclusion indeterminate (hence untrue). In the second, the counterexample is the valuation on which ‘P’ is false and ‘Q’ indeterminate.
(Nolt 410)
[Nolt then turns to a metatheorem, which covers cases like these. The metatheorem says that a sequent is invalid if it introduces a sentence letter not found in the argument. The proof seems to do the following. We consider a sequence of premises that is consistent, and a conclusion that contains a sentence letter not found in the premises. We next assume that there is some valuation that makes all premises true. Next, we consider another valuation. Like the first, it makes all the premises true. But in addition, it makes all the sentence letters of the conclusion not found in the premises have the value I. This of course will do nothing to change the fact that all the premises are true. It will only make the conclusion I, since even one instance of an I value will “contaminate” the formula or formulas of the conclusion. Thus we would have a valuation that makes the premises true and the conclusion not true. Hence furthermore, when there is a sentence letter in the conclusion not found in the premises, the argument will be invalid in Bochvar’s semantics.]
METATHEOREM: Let Φ1, ..., Φn ⊢ Ψ be a sequent of ordinary propositional logic (as defined by the formation rules of Chapter 2). Then on Bochvar's semantics, if {Φ1, ..., Φn} is consistent and Ψ contains a sentence letter not found in Φ1, ..., Φn then that sequent is invalid.
PROOF: Suppose that {Φ1, ..., Φn} is consistent and Ψ contains a sentence letter not found in Φ1, ..., Φn Since {Φ1, ..., Φn} is consistent, there is some Bochvar valuation v of Φ1, ..., Φn that makes each of these formulas true. But now consider the valuation v′, which is just like v except that in addition it assigns the value I to each of the sentence letters that appear in Ψ but not in Φ1, ..., Φn. v′ makes Φ1, ..., Φn true but Ψ indeterminate, and so v′ is a counterexample, which proves the sequent invalid.
Therefore, if {Φ1, ..., Φn} is consistent and Ψ contains a sentence letter not found in Φ1, ..., Φn, then that sequent is invalid. QED
(Nolt 410)
Nolt then notes a complication. In the metatheorem he specified that the formulas must be those of “ordinary propositional logic” (410). He explains, “The reason for this qualification is that Bochvar added a novel operator to his logic, and the metatheorem does not apply to formulas containing this novel operator” (Nolt 410).
The operator means something like, “it is true that”, and Nolt will symbolize it as ‘T’, following Susan Haack (citing: Philosophy of Logics. Cambridge: Cambridge University Press, 1978, p. 207.) T is a monadic operator like negation. We need first to fashion a formation rule to allow for its inclusion in our language:
If Φ is a formula, so is TΦ.
(Nolt 411)
And Nolt shows the truth table for this as:

(Nolt 411)
We notice, then, that only if a formula Φ is true then is it true that Φ. And thus “if Φ is false or indeterminate, then it is not true that Φ” (411).
[So as we can see from the table, whenever a formula has the T operator, its value can only be either T or F, and thus it is bivalent. So by using the T operator, we can now formulate tautologies in Bochvar’s semantics. (It seems, however, that the formulation expressing the law of excluded middle is not tautologous).]
This “truth operator” gives Bochvar’s logic a new twist, for any formula of which it is the main operator is bivalent. And though, as we saw above, Bochvar’s logic contains no tautologies among the formulas of ordinary propositional logic, it does have tautologies. These, however, are all formulas containing the truth operator. Here are some examples:
TP → TP
TP ∨ ~TP
T(P ∨ ~P) ∨ (~TP & ~T~P)
Notice, by contrast, that ‘TP ∨ T~P’ is not tautologous, for it is false when ‘P’ is indeterminate.
(Nolt 411)
Nolt explains that it was Bochvar’s hope that his T operator would resolve the semantic paradoxes [like the liar paradox] (Nolt 411). Above we called the following sentence S:
Sentence S is false.
(Nolt 411)
We had reason to think that it was neither true nor false. With Bochvar’s semantics, we can designate it as I, which means that TS would be F. [I am not certain, but it seems that this avoids the paradox for the following reason. As we know, we cannot simply designate S as true or false, because this leads to a contradiction. I do not know however what it means if we simply say that S is I, without also adding the T operator. I am just guessing, but perhaps the problem is the following. We are now saying that S is I, but S says of itself that it is false. Since what it says of itself is not what it is (as it says it is false but it was designated as I), that makes S false. But we said at first it was I, hence the contradiction. At any rate, the idea is that TS eliminates the problem, when S is I, because it makes TS simply be false in a non-problematic way. There is no paradox for TS, because TS means, ‘it is true that S is false’. The truth table tells us that when S is I, then TS is false. This means that ‘it is not true that S is false’ is true. Here there is no contradiction, because in fact it is not true that S is false, as it is I and not false. But I am just guessing at the reasoning here, so please consult the quoted text that follows after the next summarization.]
But, there is still a problem with this semantic paradox. Suppose we fashion the formula U:
Sentence U is untrue.
(411)
It cannot be true, because then it says of itself that it is untrue, which is a contradiction. [Let us first consider the difference between untrue and false in this three-valued system. To be false means to be neither true nor I. To be untrue means to be either false or I.] [The next step here is to suppose that it is either false or indeterminate. I am not sure if we also add the T operator. First let us consider it without that operator. Suppose we say that this sentence is false. That means it is also not-true and thus untrue. However, it says of itself that it is untrue, and so it would be true as well (because what it says is what is the case). So if we say it is false, it leads to a contradiction. Suppose instead its value is I. That means again it is untrue and thus (given what is says) is also true. Hence if we designate U as I, then we obtain a contradiction. Let us further consider the T operator. Suppose U is true. The formula TU, which means, ‘It is true that Sentence U is untrue’, would be true according to the truth table for T. But it says of itself that it is untrue, hence a contradiction. Suppose now that U is false. That makes TU, which means, ‘It is true that Sentence U is untrue’ be false according to the truth tables. But that would mean ‘It is not true that sentence U is untrue’ is true. And if U is not untrue, it would have to be either true or I. But we first designated U as false, so we have a contradiction. So suppose instead we designate U as I. That means, TU, which again would read ‘It is true that sentence U is untrue’ is false, according to the truth tables. But that means ‘It is not true that sentence U is untrue’ is true. And if U is not untrue, it cannot be I or false and thus must be true. However, we originally designated U as I and thus as not being true. (I had trouble following the reasoning in this section, so please consult the quotation to follow):]
Bochvar hoped that his new semantics would solve the problem of semantic paradox. Consider, for example, the semantically paradoxical sentence that we have called S:
Sentence S is false.
We argued above that S is neither true nor false. But if we adopt Bochvar's semantics, there is a third option: It might have the value I. Suppose, then, that it does. In that case, using the sentence letter ‘S’ to represent sentence S, though the formula ‘S’ has the value I, the formula ‘TS’ has the value F, for it is in fact not true that sentence S is false.
This three-valued approach seems neatly to dissolve the paradox. Unfortunately, however, a new paradox emerges to take its place. Let U be the sentence:
Sentence U is untrue.
As before, suppose for reductio that this sentence is true. Then what it says is correct, and so it is untrue. Hence it is both true and untrue – a contradiction. Therefore it is not true. It follows, on Bochvar’s semantics, that it has one of the | values F or I. But in either case it is untrue, and so what it says is correct; hence it is true. Once again we have a contradiction – despite the third value.
Bochvar’s semantics does not, therefore, provide a general solution to semantic paradoxes – nor does any other three-valued or multivalued semantics. If semantic paradox is the problem, multivalued semantics is not the solution.
(Nolt 411-412)
Nolt next turns to the second policy, where indeterminacy in a formula’s parts does not necessarily affect the whole, so long as the other parts still suffice to produce a T or F valuation under the normal rules. [So it seems that under this policy, an indeterminate value that is part of a composite formula will cause the whole formula to be indeterminate, unless the conditions for truth or falsity are sufficiently met by the other terms. So consider conjunction, which was defined on p.50 as T if both conjuncts are T, and it is F if either or both conjuncts is not true. But in these new policy tables, it seems that the rule would be that it is false iff either or both conjuncts is false (and not just untrue). In the new truth tables, we see that the conjunction’s value is true only when both conjuncts are true, and it is only false when either conjunct is false. But it is indeterminate when one is true and the other indeterminate. For, here it fulfills neither qualification. It cannot be true, because not both conjuncts are true. And it cannot be false, because neither of the conjuncts are false. It is also indeterminate when both conjuncts are indeterminate, for the same reason. Disjunctions under this new policy are true so long as at least one disjunct is true, and false only when both are false. It is indeterminate when one disjunct is false and the other indeterminate, or when both are indeterminate. Thus the criteria seems to be that a disjunct is true only when both disjuncts are true; it is false only when both are false, and it is indeterminate either when one is false and the other indeterminate or when both are indeterminate. Next is the conditional. It is false only when the antecedent is true but the consequent false. What determines whether it is true or indeterminate seems to be something like the following. If the consequent is indeterminate and the antecedent is not false, then it is indeterminate, and true otherwise. (The thinking might be that the “indeterminate” could potentially mean false, and so any situation where it is ambiguous where potentially the antecedent is true and the consequent is false means that the whole conditional is indeterminate.) Finally, consider the biconditional. This is true only if both terms are true, and it is only false if one is true and the other false. It is indeterminate if either one or both are indeterminate.]


(Nolt 412)
Nolt writes that the “three-valued propositional semantics expressed by these tables was first proposed by S. C . Kleene”, and that we can use the T operator, “which has the same truth table as before” (Nolt 412). Like with Bochvar’s semantics, Kleene’s three-valued semantics also makes all classically tautologous formulations non-tautologous, because for any of them there we can assign all the formula’s component letters as I, thereby making all formulas not true, even if they are necessarily true in classical bivalent logic.
On Kleene’s semantics, as on Bochvar’s, classically tautologous formulas are nontautologous. For, as on Bochvar’s semantics, any statement of ordinary propositional logic all of whose atomic components have the truth value I has itself the truth value I; hence, for any formula, there is always a valuation (namely, the valuation that assigns I to all of its sentence letters) on which that formula is not true.
(412)
One important difference between Kleene’s and Bochvar’s semantics is that Kleene’s “makes most of the classical inference patterns, including paradoxes of material implication, valid” (412). However, some of the classical valid inferences are invalid in Kleene’s semantics. “In particular, inferences to what are classically tautologies from irrelevant premises still fail. The sequent ‘P ⊢ Q→Q’, for example, though classically valid, is invalid on Kleene’s semantics, for the valuation on which ‘P’ is true and ‘Q’ indeterminate is a counterexample” (Nolt 412).
Łukasiewicz’s semantics makes the conditional and the biconditional true when both terms are indeterminate.
Kleene’s semantics assigns the classical values T and F to more complex formulas than Bochvar’s semantics does. Łukasiewicz, who was the first to explore three-valued logic, proposed a semantics that goes even further in this direction. Łukasiewicz’s semantics is like Kleene’s, except that where Kleene makes the conditional and biconditional indeterminate when both their components are indeterminate, Łukasiewicz makes them true. Łukasiewicz’s semantics is thus expressed by the following truth tables: |

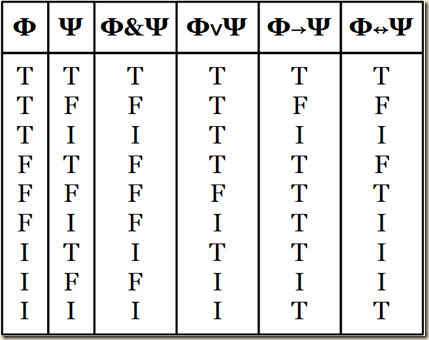
(Nolt 412-413)
And as in the other semantics, we can add the T operator to Łukasiewicz’s system (413).
Nolt then discusses which classical tautologies are made valid by Łukasiewicz’s semantics and which are not. Some examples of classical tautologies that are made true are:
P → P
P → (P ∨ Q)
(P & Q) → P
P ↔ ~~P
(Nolt 413)
[If we look at the truth tables for Łukasiewicz’s semantics, we see that all of these would be true regardless if the terms are T, F, or I.] However, the law of excluded middle and the law of noncontradiction are not tautologous.
P ∨ ~P
~(P & ~P)
(Nolt 413)
[If we look at the truth tables for Łukasiewicz’s semantics, we see that] when we assign P as I, in the first one we have an indeterminate value, and the same for the second. And thus they are not always true and hence are not tautologous. Nolt says that certain classical tautologies could become false in Łukasiewicz’s semantics, as for example:
~(P ↔ ~P)
(Nolt 413)
Łukasiewicz’s semantics makes invalid certain sequents in which there is an inference of classical tautologies from unrelated premises. “For example, ‘P ⊢ Q ∨ ~Q’ is invalid since its premise is true while its conclusion is indeterminate in the case in which ‘P’ has the value T and ‘Q’ the value I. Anomalously, however, ‘P ⊢ Q → Q’ remains valid” (413).
There are other cases in Łukasiewicz’s semantics that are potentially problematic, because they invalidate certain logical equivalences [that we intuitively would want to keep]:
Moreover, Łukasiewicz’s semantics dispenses with the classical logical equivalences between ~(Φ & ~Ψ) or ~Φ ∨ Ψ and Φ → Ψ, precisely because of this case. For although Φ → Ψ is true when both Φ and Ψ are indeterminate, both ~(Φ & ~Ψ) and ~Φ ∨ Ψ are indeterminate in that case. Some logicians find these features inelegant.
(Nolt 413)
Nolt says that more than three values are possible, even infinitely many. He gives an example for four-valued logic: “Some of the early semantics for modal logic, for example, used four values: contingently true, contingently false, necessarily true, and necessarily false, with the first two as designated values” (Nolt 413). But he says there are too many such variants to mention here (413).
Nolt says that we can also construct multivalued predicate logics, which often involves making some choices regarding the way atomic formulas are to be evaluated.
One can also, of course, create multivalued predicate logics. This generally requires some adjustment of the definition of a valuation and of the valuation rules for atomic formulas. We might, for example, as in free logics, allow names to lack referents. Then either all or some of the formulas containing these names could be stipulated to have the truth value I. Or we could attempt to dichotomize atomic | formulas into those that are meaningful and those that are meaningless, assigning the latter the value I. Or, if we are doing tense logic, we might design our models so that atomic statements about the future always receive the value I. But again, we shall not bother with the details of these variations.
(413-414)
From:
Nolt, John. Logics. Belmont, CA: Wadsworth, 1997.
.


.jpeg)