[Search Blog Here. Index-tags are found on the bottom of the left column.]
[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]
Summary of
David W. Agler
Symbolic Logic: Syntax, Semantics, and Proof
Ch.7: Predicate Logic Trees
7.3 Logical Properties
Brief summary:
Truth trees can determine logical properties of singular propositions, sets of propositions, and arguments in the language of predicate logic (RL). To test a proposition to see if it is a contradiction, we see if it makes a closed tree. If and only if it does is it a contradiction. To test a proposition to see if it is a tautology, we make a tree for its negation. If and only if it makes a closed tree is the original proposition a tautology. If it fails both these tests, it is a contingency. To check for the consistency of sets of propositions, we see if their tree has at least one open branch. If so, they are consistent. If instead the tree is closed, then they are inconsistent. To test for the validity of an argument, we negate the conclusion and make a tree for the full set of sentences. If they determine a closed tree, the original argument was valid. If it determines a tree with at least one completed open branch, it is invalid.
Summary
7.3 Logical Properties
7.3 Logical Properties
We will now learn how to use truth trees to determine if propositions, sets of propositions, or arguments have one or another logical property. [Recall from section 4.2.2 in our discussion of truth trees for the language of propositional logic (PL) the following terms. Branch: “A branch includes all the propositions obtained by starting from the bottom of the tree and reading upward through the tree” (109). Fully decomposed branch: “A branch is fully decomposed when all propositions in the branch that can be decomposed have been decomposed” (110). Partially decomposed branch: “A branch is partially decomposed when there is at least one proposition in the branch that has not been decomposed” (110). Closed branch: “A closed branch contains a proposition ‘P’ and its literal negation ‘¬P.’ A closed branch is represented by an ‘X’ ” (111). Open branch: “An open branch is a branch that is not closed, that is, a branch that does not contain a proposition ‘P’ and its literal negation ‘¬P’ ” (111). Completed open branch: “A completed open branch is a fully decomposed branch that is not closed. That is, it is a fully decomposed branch that does not contain a proposition and its literal negation. An open branch is denoted by writing an ‘0’ at the bottom of the tree” (112). Completed open tree: “A tree is a completed open tree if and only if it has at least one completed open branch. That is, a tree is a completed open tree if and only if it contains at least one fully decomposed branch that is not closed. A completed open tree is a tree where there is at least one branch that has an ‘0’ under it” (113). Closed tree: “A tree is closed when all of the tree’s branches are closed. A closed tree will have an ‘X’ under every branch” (114).] In order to do this, Agler will first redefine what a completed open branch is in RL, and he will explain how “analyzing trees in RL is different from analyzing trees in PL” (Agler 294). Agler defines completed open branch, closed tree, and closed branch in the following ways for RL.
To illustrate what makes a completed open branch, Agler first shows one that looks like it could be an example but in fact is not.Completed open branch: A branch is a completed open branch if and only if (1) all complex propositions that can be decomposed into atomic propositions or negated atomic propositions are decomposed; (2) for all universally quantified propositions ‘(∀x)P’ occurring in the branch, there is a substitution instance ‘P(a/x)’ for each constant that occurs in that branch; and (3) the branch is not a closed branch.Closed tree: A tree is a closed tree if and only if all branches close.Closed branch: A branch is a closed branch if and only if there is a proposition and its literal negation (e.g., ‘P’ and ‘¬P’).(Agler 294)
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃x)(Px∧¬Qx)✔ | P |
| 3 | Pa→Qa✔ | 1∀D |
| 4 | Pb∧¬Qb✔ | 2∃D |
| 5 | Pb | 4∧D |
| 6 | ¬Qb / \ / \ | 4∧D |
| 7 | ¬Pa Qa | 3→D |
(Agler 294)
The reason we have not followed the procedure is because we did not fulfill this part of the definition of a completed open branch.
For all universally quantified propositions ‘(∀x)P’ occurring in the branch, there is a substitution instance ‘P(a/x)’ for each constant that occurs in that branch.(294d)
We still need to decompose line one with respect to constant ‘b’, which we use higher in the branch.
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃x)(Px∧¬Qx)✔ | P |
| 3 | Pa→Qa✔ | 1∀D |
| 4 | Pb∧¬Qb✔ | 2∃D |
| 5 | Pb | 4∧D |
| 6 | ¬Qb / \ / \ | 4∧D |
| 7 | ¬Pa Qa | 3→D |
| 8 | Pb→Qb Pb→Qb / \ / \ | 1∀D |
| 9 | ¬Pb Qb ¬Pb Qb X X X X | 8→D |
(Agler 295, with justification added to line 8, perhaps incorrectly)
As we can see, when we follow the procedure properly, we find that these formulas produce a closed rather than an open tree (Agler 295).
Agler then has us consider the following propositions.
(∀x)(¬Px→¬Rx), (∀x)(Rx→Px)(Agler 295)
Let us first set them up.
| 1 | (∀x)(¬Px→¬Rx) | P |
| 2 | (∀x)(Rx→Px) | P |
Recall the strategic decomposition rules from section 7.2. We should first decompose negated quantified and existential expressions. But as we can see, we have none here. So we should use universal decomposition. Since we do not have any constants in the tree so far, we arbitrarily pick ‘a’.
| 1 | (∀x)(¬Px→¬Rx) | P |
| 2 | (∀x)(Rx→Px) | P |
| 3 | ¬Pa→¬Ra | 1∀D |
[At this point we have a choice. We could universally decompose line 2, or we could use conditional decomposition on line 3. Agler will decompose line 2. Perhaps this is because universal decomposition is a stacking rule, and we should do stacking before branching rules.]
| 1 | (∀x)(¬Px→¬Rx) | P |
| 2 | (∀x)(Rx→Px) | P |
| 3 | ¬Pa→¬Ra | 1∀D |
| 4 | Ra→Pa | 2∀D |
Now we can decompose the conditionals, one at a time.
| 1 | (∀x)(¬Px→¬Rx) | P |
| 2 | (∀x)(Rx→Px) | P |
| 3 | ¬Pa→¬Ra✔ | 1∀D |
| 4 | Ra→Pa✔ / \ | 2∀D |
| 5 | ¬¬Pa ¬Ra / \ / \ | 3→D |
| 6 | ¬Ra Pa ¬Ra Pa O O O O | 4→D |
(Agler 295)
[Recall these definitions from before: “Closed branch: A branch is a closed branch if and only if there is a proposition and its literal negation (e.g., ‘P’ and ‘¬P’);” “Completed open branch: A branch is a completed open branch if and only if (1) all complex propositions that can be decomposed into atomic propositions or negated atomic propositions are decomposed; (2) for all universally quantified propositions ‘(∀x)P’ occurring in the branch, there is a substitution instance ‘P(a/x)’ for each constant that occurs in that branch; and (3) the branch is not a closed branch” (Agler 294). As we can see, we have fulfilled the requirements for a completed open branch.] We only have one constant, ‘a’. So our universal decompositions have made all substitutions for constants in the branches. Thus even though we have not checked off our universally quantified formulas, we have completed the tree, and since all the branches are open, it is a completed open tree (Agler 296a).
7.3.1 Semantic Analysis of Predicate Truth Trees
[In PL, we performed semantic analysis by taking into consideration the truth or falsity of propositions. But in RL, the matter is not so simple. We will need to specify the domain of discourse and an interpretation function to determine the truth and falsity of formulas.]
In PL, the basic unit of representation is the proposition, which is assigned a truth value (true or false). In RL, the truth or falsity of a predicate well-formed formula (wff, pronounced ‘woof’) is relative to an interpretation in a model (i.e., relative to a specification of the domain of discourse and an interpretation function). Using the notion of an interpretation, semantic properties can be defined for RL propositions, sets of propositions, and arguments as follows:Tautology: A proposition ‘P’ is a tautology in RL if and only if ‘P’ is true on every interpretation.Contradiction: A proposition ‘P’ is a contradiction in RL if and only if ‘P’ is false on every interpretation.Contingency: A proposition ‘P’ is a contingency in RL if and only if ‘P’ is neither a contradiction nor a tautology.Equivalence Propositions: ‘P’ and ‘Q’ are equivalent in RL if and only if there is no interpretation where the valuation of ‘P’ is different from the valuation of ‘Q.’Consistency: A set of propositions ‘{A, B, C, ..., Z}’ is consistent in RL if and only if there is at least one interpretation such that all of the propositions in the set are true.Validity: An argument ‘P, Q, R, ..., Y⊢Z’ is valid in RL if and only if there is no interpretation such that all of the premises ‘A,’ ‘B,’ ‘C,’ ..., ‘Y’ are true and the conclusion ‘Z’ is false.(Agler 296)
To see if a proposition, a set of propositions, or an argument has any of these properties, we can construct a model and test it. Agler has us consider these propositions:
(∀x)Px(∃x)Rx(Agler 296)
Suppose we wanted to know if they are consistent. [Recall the definition for consistency. “Consistency: A set of propositions ‘{A, B, C, ..., Z}’ is consistent in RL if and only if there is at least one interpretation such that all of the propositions in the set are true.”] This means we need to find at least one interpretation that makes both formulas true. [If we make the domain be all positive integers, and we furthermore make the predicate P mean “is greater than 0” and R “is even”, then we have found a domain and interpretation function that makes both propositions true. For, all positive integers are greater than zero, and there is at least one (in fact infinitely many) that are even.]
to show that ‘{(∀x)Px, (∃x)Rx}’ is consistent in RL involves showing that there is at least one interpretation in a model where v(∀x)Px = T and v(∃x)Rx = T. Here is an example of such a model:D = positive integersP = {x | x is greater than 0}R = {x | x is even}(Agler 296)
We will see now how to use truth trees to determine the logical properties we are interested in. Just like in PL, a completed open branch in RL means that we have a truth-value assignment that makes every proposition in the stack true. “Thus, the presence of a completed open branch tells us that we can construct a model such that every proposition in the stack is true” (Agler 297). Agler has us consider these formulas.
| 1 | (∃x)Px | P |
| 2 | Pa | P |
Here we just have the existentially quantified formula in line one to decompose. Since we already used the constant ‘a’, we need now to pick another one.
| 1 | (∃x)Px | P |
| 2 | Pa | P |
| 3 | Pb | 1∃D |
[Again recall what qualifies as a completed open branch: “Completed open branch: A branch is a completed open branch if and only if (1) all complex propositions that can be decomposed into atomic propositions or negated atomic propositions are decomposed; (2) for all universally quantified propositions ‘(∀x)P’ occurring in the branch, there is a substitution instance ‘P(a/x)’ for each constant that occurs in that branch; and (3) the branch is not a closed branch.”] This branch is then completed open.
| 1 | (∃x)Px | P |
| 2 | Pa | P |
| 3 | Pb O | 1∃D |
(Agler 297)
And since it is completed open, that means there is some interpretation that will make all the propositions in that branch true. That furthermore means we can “construct an interpretation in a model that would show ‘(∃x)Px,’ ‘Pa,’ and ‘Pb’ as being consistent” (Agler 297). [In our branch, we just have two object, ‘a’ and ‘b’.] For the purpose of showing that the propositions are consistent,
we would stipulate a domain of discourse involving two objects, letting ‘a’ stand for an object and ‘b’ stand for an object, and assign the one-place predicate ‘P’ an extension.D: {John, Fred}Px: x is a person {John, Fred}a: Johnb: Fred(Agler 297)
So we see that the interpretational function would assign x to either John or Fred. This means that Pa and Pb are true, because both ‘a’ and ‘b’ are people. That furthermore means that (∃x)Px is true, because there is at least one item in the domain which takes the predicate P.
Agler has us consider now these propositions.
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px | P |
[Let us recall the rules for decomposition. “1. Use no more rules than needed. 2. Decompose negated quantified expressions and existentially quantified expressions first. 3. Use rules that close branches. 4. Use stacking rules before branching rules. 5. When decomposing universally quantified propositions, use constants that already occur in the branch. 6. Decompose more complex propositions before simpler propositions” (Agler 291). We might first be inclined to decompose line 1, since it is a stacking rule, which should come first (rule 4). However, we know already that implied in rule 5 is the idea that we should decompose existentially quantified formulas first, because that will minimize the number of decompositions we will have to do. (Were we to start with the existentially quantified sentence, then we would generate an additional constant that would need to later be placed into the universal decomposition.) So this means we should decompose the existential quantifiers in line 2. In order to do that, we should first decompose the main operator, using disjunction decomposition.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
(Agler 298)
[We now have a choice of three things to decompose. Since we still have existentially quantified formula, we should do those still before the universally quantified one. At this point, it seems arbitrary which branch we decompose first. Both would take stacking rules. So let us begin with the left branch.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
[Now on this left branch, in order to complete it, we still need to decompose the universally quantified expression of line 1. We have only one constant on this branch, ‘a’.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
| 5 | Pa | | 1∀D |
[We have done everything we need to do to complete this branch. Since there are no contradictions, it is a completed open branch.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
| 5 | Pa | O | 1∀D |
[Now let us decompose the other branch. This time we begin with negated existential decomposition.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
| 5 | Pa | O | | 1∀D |
| 6 | (∀x)¬Px | 3¬∃D |
[We now have two universally quantified formulas to decompose, one in line 1 and one in line 6. It is arbitrary which comes first.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
| 5 | Pa | O | | 1∀D |
| 6 | (∀x)¬Px | 3¬∃D |
| 7 | ¬Pa | 6∀D |
| 8 | Pa | 1∀D |
[As we can see, we have a formula and its negation in lines 7 and 8, which means the branch closes.]
| 1 | (∀x)Px | P |
| 2 | (∃x)Px∨¬(∃x)Px / \ | P |
| 3 | (∃x)Px ¬(∃x)Px | 2∨D |
| 4 | Pa | | 3∃D |
| 5 | Pa | O | | 1∀D |
| 6 | (∀x)¬Px | 3¬∃D |
| 7 | ¬Pa | 6∀D |
| 8 | Pa O | 1∀D |
(Agler 298)
[Note. I am not sure why we do not place a checkmark for line 2 or for line 3.] The fact that the right branch is closed means that “there is no interpretation for which ‘¬(∃x) Px’ and ‘(∀x)Px’ are true” (298). [See lines 1 and 3.] But the right branch is completed open. So we can construct an interpretation in a model making all propositions in the right branch true. [To make lines 1 and 2 true, we just need to say that there exists at least one thing in the domain that fulfuils some property.] Agler offers this model:
D: {1}Px: x is a number(Agler 298)
Agler then has us consider a more complicated proposition.
| 1 | (∃x)(∃y)[(Ox∧Ey)∧Gxy] | P |
[Since the leftmost existential quantifier is the main operator, we will begin by decomposing it first.]
| 1 | (∃x)(∃y)[(Ox∧Ey)∧Gxy]✔ | P |
| 2 | (∃y)[(Oa∧Ey)∧Gay] | 1∃D |
[For the same reason, we now decompose the existential quantifier in line 2.]
| 1 | (∃x)(∃y)[(Ox∧Ey)∧Gxy]✔ | P |
| 2 | (∃y)[(Oa∧Ey)∧Gay]✔ | 1∃D |
| 3 | (Oa∧Eb)∧Gab | 2∃D |
[Now that the quantifiers have been eliminated, we will decompose the rest using the other rules of decomposition. Here we just have a series of conjunction decompositions to do.]
| 1 | (∃x)(∃y)[(Ox∧Ey)∧Gxy]✔ | P |
| 2 | (∃y)[(Oa∧Ey)∧Gay]✔ | 1∃D |
| 3 | (Oa∧Eb)∧Gab✔ | 2∃D |
| 4 | Oa∧Eb✔ | 3∧D |
| 5 | Gab | 3∧D |
| 6 | Oa | 4∧D |
| 7 | Eb | 4∧D |
| 1 | (∃x)(∃y)[(Ox∧Ey)∧Gxy]✔ | P |
| 2 | (∃y)[(Oa∧Ey)∧Gay]✔ | 1∃D |
| 3 | (Oa∧Eb)∧Gab✔ | 2∃D |
| 4 | Oa∧Eb✔ | 3∧D |
| 5 | Gab | 3∧D |
| 6 | Oa | 4∧D |
| 7 | Eb O | 4∧D |
(Agler 298)
Since it is an open completed branch,
there is an interpretation for which the propositions ‘Gab,’ ‘Oa,’ and ‘Eb’ are true, and thus ‘(∃x)(∃y) [(Ox∧Ey)∧Gxy]’ is true. Again, a model can be constructed to reflect this fact:D: {1, 2, 3}Ox: x is an odd numberEx: x is an even numberGxy: x is greater than ya: 3b: 2‘Gab’ is true since it is true that 3 is greater than 2. ‘Oa’ is true since three is an odd number. Lastly, ‘Eb’ is true since 2 is an even number. Thus, the predicate wff ‘(∃x)(∃y)[(Ox∧Ey)∧Gxy],’ which says that there exists an odd number greater than | some existent even number, is also true. In short, the truth tree, along with the model, demonstrates that the set ‘{(∃x)(∃y)[(Ox∧Ey)∧Gxy]}’ is not a contradiction in RL.(Agler 298-299)
From this point on, Agler will no longer be formulating models to show ways that completed open branches have models that make the propositions true. Instead we focus on ways to use the trees themselves to determine logical properties (Agler 299).
7.3.2 Consistency and Inconsistency
Consistency and inconsistency are properties that sets of propositions can hold.
Consistency: A set of propositions ‘{P, Q, R, ..., Z}’ is shown by the truth-tree method to be consistent if and only if a tree of the stack ‘P,’ ‘Q,’ ‘R,’ . . ., ‘Z’ is an open tree; that is, there is at least one completed open branch.
Inconsistency: A set of propositions ‘{P, Q, R, ..., Z}’ is shown by the truth-tree method to be inconsistent if and only if a tree of the stack of ‘P,’ ‘Q,’ ‘R,’ . . ., ‘Z’ is a closed tree; that is, all branches close.
(Agler 299)
Agler first will show us a tree for inconsistent propositions.
(∀x)(Px→Rx), ¬(∀x)(¬Rx→¬Px)(Agler 299)
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px) | P |
[Since line 2 is a negated quantified expression, we should start with it.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px) | 2¬∀D |
[And we should do the existentially quantified expressions before the universally quantified ones.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
[This leaves us with the universally quantified expression and the negated conditional. Both of these are stacking, so it would seem arbitrary which to do next. We will just do the universally quantified one first. Or perhaps there is a reason we need to do quantifications first, but I am not sure.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
| 5 | Pa→Ra | 1∀D |
[Now we again have two choices, namely, to decompose the conditional in line 5 or the negated conditional in line 4. Since the negation conditional decomposition is stacking, we do that next.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
| 5 | Pa→Ra✔ | 1∀D |
| 6 | ¬Ra | 4¬→D |
| 7 | ¬¬Pa | 4¬→D |
[This gives us a double negation that we should decompose.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
| 5 | Pa→Ra✔ | 1∀D |
| 6 | ¬Ra | 4¬→D |
| 7 | ¬¬Pa✔ | 4¬→D |
| 8 | Pa | 7¬¬D |
(based on Agler 299, with checkmark – perhaps mistakenly – added to line 7)
[This leaves us with just one proposition to decompose, namely, the conditional in line 5.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
| 5 | Pa→Ra✔ | 1∀D |
| 6 | ¬Ra | 4¬→D |
| 7 | ¬¬Pa✔ | 4¬→D |
| 8 | Pa / \ | 7¬¬D |
| 9 | ¬Pa Ra | 5→D |
(based on Agler 299, with checkmark – perhaps mistakenly – added to line 7)
[As we can see, in the left branch, line 9 contradicts line 8, and in the right branch, line 9 contradicts line 6. Thus both are closed.]
| 1 | (∀x)(Px→Rx) | P |
| 2 | ¬(∀x)(¬Rx→¬Px)✔ | P |
| 3 | (∃x)¬(¬Rx→¬Px)✔ | 2¬∀D |
| 4 | ¬(¬Ra→¬Pa) | 3∃D |
| 5 | Pa→Ra✔ | 1∀D |
| 6 | ¬Ra | 4¬→D |
| 7 | ¬¬Pa✔ | 4¬→D |
| 8 | Pa / \ | 7¬¬D |
| 9 | ¬Pa Ra | 5→D |
(Agler 299, with checkmark – perhaps mistakenly – added to line 7)
Thus this tree shows the original propositions to be inconsistent (Agler 299).
Agler then has us consider these propositions.
| 1 | (∀x)(Px)→(∀y)(Ry) | P |
| 2 | ¬(∀y)Ry | P |
| 3 | (∃x)¬Px | P |
[According to our strategic rules, we should do row 2 or 3 first. Perhaps it is arbitrary, so we will start with 2.]
| 1 | (∀x)(Px)→(∀y)(Ry) | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px | P |
| 4 | (∃y)¬Ry | 2¬∀D |
[Next we should do the existentially quantified expressions in lines 3 and 4. Since it seems arbitrary which one, we will begin with 4 and then do 3.]
| 1 | (∀x)(Px)→(∀y)(Ry) | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb | 3∃D |
[This leaves us with line 1 to decompose. Perhaps we could decompose each universal quantifier within the conditional. Agler will first decompose the conditional, presumably because it is the main operator. I have the impression that Agler’s methodologies deal with each formula’s main operators primarily.]
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px (∀y)Ry | 1→D |
[We can work now on the left branch. First we use negated universal decomposition.]
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px✔ (∀y)Ry | 1→D |
| 8 | (∃x)¬Px | | 7¬∀D |
[Then we use existential decomposition on line 8. Since we already used constants ‘a’ and ‘b’, we will here use ‘c’.]
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px✔ (∀y)Ry | 1→D |
| 8 | (∃x)¬Px✔ | | 7¬∀D |
| 9 | ¬Pc | | 8∃D |
[We have nothing left to decompose along this branch. There is no contradiction, so it is a completed open branch.]
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px✔ (∀y)Ry | 1→D |
| 8 | (∃x)¬Px✔ | | 7¬∀D |
| 9 | ¬Pc | O | | 8∃D |
[At this point perhaps we can stop, because by finding at least one completed open branch, we have determined that the propositions are consistent. But we will continue with the right branch. We have two constants along the right branch, namely, ‘a’ and ‘b’.
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px✔ (∀y)Ry | 1→D |
| 8 | (∃x)¬Px✔ | | 7¬∀D |
| 9 | ¬Pc | O | | 8∃D |
| 10 | Ra | 7∀D |
| 11 | Rb | 7∀D |
[As we can see, line 10 contradicts line 5, so it is a closed branch.]
| 1 | (∀x)(Px)→(∀y)(Ry)✔ | P |
| 2 | ¬(∀y)Ry✔ | P |
| 3 | (∃x)¬Px✔ | P |
| 4 | (∃y)¬Ry✔ | 2¬∀D |
| 5 | ¬Ra | 4∃D |
| 6 | ¬Pb / \ | 3∃D |
| 7 | ¬(∀x)Px✔ (∀y)Ry | 1→D |
| 8 | (∃x)¬Px✔ | | 7¬∀D |
| 9 | ¬Pc | O | | 8∃D |
| 10 | Ra | 7∀D |
| 11 | Rb X | 7∀D |
(Agler 300)
Agler then has us consider these propositions.
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy) | P |
| 2 | ¬(∀y)(∀x)(Rxy) | P |
| 3 | (Rab∧Rba)∧Pab | P |
[Agler begins with line 3. Perhaps this is because it has constants, but I am not sure, because line 2 has a negated quantified expression that could also come first. Let us decompose line three until we obtain atomic propositions.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy) | P |
| 2 | ¬(∀y)(∀x)(Rxy) | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
[At this point we have two choices, namely, lines 1 and 2. Agler will do l ine 1 first.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy) | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy) | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
[Now we have two negated quantifiers to decompose, in lines 8 and 2.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy) | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy) | 2¬∀D |
[As main operators, we now have a choice of two existential quantifiers and a universal one. So we begin with the existential one in line 10.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy) | 2¬∀D |
| 12 | ¬(∃y)(Pcy) | 10∃D |
[This now gives us a negated quantifier, which we should decompose next.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy) | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy) | 12¬∃D |
[Our options now are the universal quantifier in line 9, the existential quantifier in line 10, and the universal quantifier in line 13. As far as I recall, we are supposed to do the existential ones first. But for one reason or another, Agler will do the universal in line 13. Perhaps it is arbitrary or advantageous for some reason. It already has the constant ‘c’ at the x place. And we have three constants to substitute in for y, namely, ‘a’, ‘b’, and ‘c’.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy) | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
[Our options are now the universal in line 9 and the existential in line 11. We should do the existential first. Even though we have not used constant ‘d’ yet, Agler for one reason or another goes to ‘e’, but it makes no difference.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe) | 11∃D |
[Since that gives us a negated quantifier, we should do that next.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe)✔ | 11∃D |
| 18 | (∃x)¬(Rxe) | 17¬∀D |
[Now we have an existential quantifier that we should decompose next.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy) | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe)✔ | 11∃D |
| 18 | (∃x)¬(Rxe)✔ | 17¬∀D |
| 19 | ¬Rfe | 18∃D |
[This leaves us with the universal quantifier in line 9. I am not sure why, but Agler does not decompose it using the constant ‘c’. I will not add it, but we might imagine an extra decomposition perhaps at line 22 where we substitute ‘c’ in for the y.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy)✔ | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe)✔ | 11∃D |
| 18 | (∃x)¬(Rxe)✔ | 17¬∀D |
| 19 | ¬Rfe | 18∃D |
| 20 | ¬(∃x)(Rxa) | 9∀D |
| 21 | ¬(∃x)(Rxb) | 9∀D |
| 22 | ¬(∃x)(Rxe) | 9∀D |
| 23 | ¬(∃x)(Rxf) | 9∀D |
[We now can use decompose all these negated existential quantifiers. Again, we might also imagine one for the constant ‘c’, if in fact we were to add it.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy)✔ | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe)✔ | 11∃D |
| 18 | (∃x)¬(Rxe)✔ | 17¬∀D |
| 19 | ¬Rfe | 18∃D |
| 20 | ¬(∃x)(Rxa)✔ | 9∀D |
| 21 | ¬(∃x)(Rxb)✔ | 9∀D |
| 22 | ¬(∃x)(Rxe)✔ | 9∀D |
| 23 | ¬(∃x)(Rxf)✔ | 9∀D |
| 24 | (∀x)¬(Rxa) | 20¬∃D |
| 25 | (∀x)¬(Rxb) | 21¬∃D |
| 26 | (∀x)¬(Rxe) | 22¬∃D |
| 27 | (∀x)¬(Rxf) | 23¬∃D |
[At this point, we will not need to decompose all the remaining universal quantifiers. If we can find one that raises a contradiction, we just need to decompose that one. We see that we have Rab in line 6, so we can decompose line 25 to contradict it.]
| 1 | ¬(∀x)(∃y)(Pxy)∧(∀y)¬(∃x)(Rxy)✔ | P |
| 2 | ¬(∀y)(∀x)(Rxy)✔ | P |
| 3 | (Rab∧Rba)∧Pab ✔ | P |
| 4 | Rab∧Rba✔ | 3∧D |
| 5 | Pab | 3∧D |
| 6 | Rab | 4∧D |
| 7 | Rba | 4∧D |
| 8 | ¬(∀x)(∃y)(Pxy)✔ | 1∧D |
| 9 | (∀y)¬(∃x)(Rxy)✔ | 1∧D |
| 10 | (∃x)¬(∃y)(Pxy)✔ | 8¬∀D |
| 11 | (∃y)¬(∀x)(Rxy)✔ | 2¬∀D |
| 12 | ¬(∃y)(Pcy)✔ | 10∃D |
| 13 | (∀y)¬(Pcy)✔ | 12¬∃D |
| 14 | ¬Pca | 13∀D |
| 15 | ¬Pcb | 13∀D |
| 16 | ¬Pcc | 13∀D |
| 17 | ¬(∀x)(Rxe)✔ | 11∃D |
| 18 | (∃x)¬(Rxe)✔ | 17¬∀D |
| 19 | ¬Rfe | 18∃D |
| 20 | ¬(∃x)(Rxa)✔ | 9∀D |
| 21 | ¬(∃x)(Rxb)✔ | 9∀D |
| 22 | ¬(∃x)(Rxe)✔ | 9∀D |
| 23 | ¬(∃x)(Rxf)✔ | 9∀D |
| 24 | (∀x)¬(Rxa) | 20¬∃D |
| 25 | (∀x)¬(Rxb) | 21¬∃D |
| 26 | (∀x)¬(Rxe) | 22¬∃D |
| 27 | (∀x)¬(Rxf) | 23¬∃D |
| 28 | ¬Rab | 25∀D |
(Agler 301-302)
7.3.3 Tautology, Contradiction, and Contingency
We now will see how to use truth trees to determine if a singular predicate proposition is a tautology, a contradiction, or a contingency. Agler defines them in this way.
Tautology: A proposition ‘P’ is shown by the truth-tree method to be a tautology if and only if the tree ‘¬P’ determines a closed tree; that is, all branches close.Contradiction: A proposition ‘P’ is shown by the truth-tree method to be a contradiction if and only if the tree ‘P’ determines a closed tree; that is, all branches close.Contingency: A proposition ‘P’ is shown by the truth-tree method to be a contingency if and only if ‘P’ is neither a tautology nor a contradiction; that is, the tree of ‘P’ does not determine a closed tree, and the tree of ‘¬P’ does not determine a closed tree.(Agler 305)
[Recall from section 4.6.3 the procedure for determining a sentence as either tautology, contradiction, or contingency in PL.
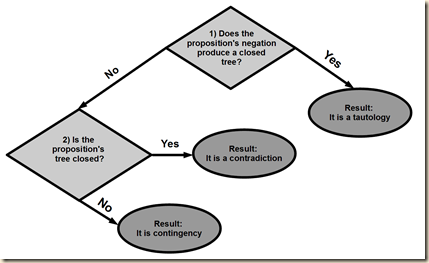
“To summarize, the truth-tree method can be used to determine whether a proposition ‘P’ is a tautology, contradiction, or contingency. In testing ‘P’ to see if it is a tautology, begin the tree with ‘¬P.’ If the tree closes, you know that it is a tautology. If the tree is open, then ‘P’ is either a contradiction or a contingency. Similarly, in testing ‘P’ to see if it is a contradiction, begin the tree with ‘P.’ If the tree closes, you know that it is a contradiction. If the tree is open, then ‘P’ is either a tautology or a contingency. Lastly, if the truth-tree test shows that ‘P’ is neither a contradiction nor a tautology, then ‘P’ is a contingency” (Agler 147). Perhaps another way would be first to test if it is a contingency by seeing if it makes a closed tree. If the tree is closed, then it is a contradiction. If it is not, then we do another test. We negate the proposition and see if it makes a closed tree. If it does, then it is a tautology. If it does not, then it is a contingency.] We will now look at a proposition and see if it is a contradiction, which we do by seeing if all the branches close.
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)] | p |
[There is just this one proposition, and as I understand, we always work with main operators, so we do existential decomposition.]
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | p |
| 2 | ¬(∀y)[Pa→(Qa∨¬Ry)] | 1∃D |
[Our next only option would be the negated universal quantifier.]
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | p |
| 2 | ¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 1∃D |
| 3 | (∃y)¬[Pa→(Qa∨¬Ry)] | 2¬∀D |
[This leaves us with the existential quantifier.]
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | p |
| 2 | ¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 1∃D |
| 3 | (∃y)¬[Pa→(Qa∨¬Ry)]✔ | 2¬∀D |
| 4 | ¬[Pa→(Qa∨¬Rb)] | 3∃D |
[We now can decompose the negated conditional.]
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | p |
| 2 | ¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 1∃D |
| 3 | (∃y)¬[Pa→(Qa∨¬Ry)]✔ | 2¬∀D |
| 4 | ¬[Pa→(Qa∨¬Rb)]✔ | 3∃D |
| 5 | Pa | 4¬→D |
| 6 | ¬(Qa∨¬Rb) | 4¬→D |
[And now we have a negated conjunction to decompose.]
| 1 | (∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | p |
| 2 | ¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 1∃D |
| 3 | (∃y)¬[Pa→(Qa∨¬Ry)]✔ | 2¬∀D |
| 4 | ¬[Pa→(Qa∨¬Rb)]✔ | 3∃D |
| 5 | Pa | 4¬→D |
| 6 | ¬(Qa∨¬Rb)✔ | 4¬→D |
| 7 | ¬Qa | 6¬∨D |
| 8 | ¬¬Rb | 6¬∨D |
(Agler 306, with corrections from handout 6)
[Note, the double negation is not further decomposed, and there is not an O noting an open branch.] Since there is at least one completed open branch, the formula is not a contradiction.
We next test if it is a tautology by seeing if its negation makes a tree with all its branches closing.
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)] | P |
[We next decompose the negated quantifier.]
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)] | 1¬∃D |
[The next main operator is the universal quantifier.]
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)] | 2∀D |
[We should now remove the double negation.]
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
[Next we have the main operator, the universal quantifier.]
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
| 5 | Pa→(Qa∨¬Ra) | 4∀D |
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
| 5 | Pa→(Qa∨¬Ra) / \ | 4∀D |
| 6 | ¬Pa Qa∨¬Ra | 5→D |
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
| 5 | Pa→(Qa∨¬Ra) / \ | 4∀D |
| 6 | ¬Pa Qa∨¬Ra O | 5→D |
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
| 5 | Pa→(Qa∨¬Ra) / \ | 4∀D |
| 6 | ¬Pa Qa∨¬Ra✔ O / \ | 5→D |
| 7 | Qa ¬Ra | 6∨D |
| 1 | ¬(∃x)¬(∀y)[Px→(Qx∨¬Ry)]✔ | P |
| 2 | (∀x)¬¬(∀y)[Px→(Qx∨¬Ry)]✔ | 1¬∃D |
| 3 | ¬¬(∀y)[Pa→(Qa∨¬Ry)]✔ | 2∀D |
| 4 | (∀y)[Pa→(Qa∨¬Ry)] | 3¬¬D |
| 5 | Pa→(Qa∨¬Ra) / \ | 4∀D |
| 6 | ¬Pa Qa∨¬Ra✔ O / \ | 5→D |
| 7 | Qa ¬Ra O O | 6∨D |
(Agler 306)
Since the above tree is not closed, the original form is not a tautology. Since it is neither a contradiction nor a tautology, it is therefore a contingency. Agler will perform these tests for the following proposition.
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx) | P |
[Our main operator is the conjunction, so we decompose that.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx) | 1∧D |
[We now have the choice of the universally and existentially quantified formulas. We should normally do the existential one first.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx)✔ | 1∧D |
| 4 | Pa∧¬Qa | 3∃D |
[We can now decompose this conjunction.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx)✔ | 1∧D |
| 4 | Pa∧¬Qa✔ | 3∃D |
| 5 | Pa | 4∧D |
| 6 | ¬Qa | 4∧D |
[This leaves us with the universal quantifier in line 2.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx)✔ | 1∧D |
| 4 | Pa∧¬Qa✔ | 3∃D |
| 5 | Pa | 4∧D |
| 6 | ¬Qa | 4∧D |
| 7 | Pa→Qa | 2∀D |
[And we decompose now this conditional.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx)✔ | 1∧D |
| 4 | Pa∧¬Qa✔ | 3∃D |
| 5 | Pa | 4∧D |
| 6 | ¬Qa | 4∧D |
| 7 | Pa→Qa✔ / \ | 2∀D |
| 8 | ¬Pa Qa | 7→D |
(based on Agler 307, with checkmark added – perhaps mistakenly – to line 7)
[As we can see, the formulas in line 8 contradict earlier lines 5 and 6.]
| 1 | (∀x)(Px→Qx)∧(∃x)(Px∧¬Qx)✔ | P |
| 2 | (∀x)(Px→Qx) | 1∧D |
| 3 | (∃x)(Px∧¬Qx)✔ | 1∧D |
| 4 | Pa∧¬Qa✔ | 3∃D |
| 5 | Pa | 4∧D |
| 6 | ¬Qa | 4∧D |
| 7 | Pa→Qa✔ / \ | 2∀D |
| 8 | ¬Pa Qa X X | 7→D |
(Agler 307, with checkmark added – perhaps mistakenly – to line 7)
As we can see, all the branches close, which means the original proposition is a contradiction (Agler 307).
We next want to test the following formula to see if it is a tautology.
(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)(Agler 307)
To do so, we first negate it, and then we see if it creates a closed tree.
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)] | P |
[We here just have the option of decomposing the negated conjunction.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px) ¬(∀y)(Qy∨¬Qy) | 1¬∧D |
(based on Agler 307. Here and in the following, a loose left bracket is removed from the right branch of line 2]
[We now have two negated quantifiers, which we can dually decompose in the next line.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px)✔ ¬(∀y)(Qy∨¬Qy✔ | 1¬∧D |
| 3 | (∃x)¬(Px→Px) (∃y)¬(Qy∨¬Qy) | 2¬∀D |
[We now have two existential quantifiers that we can dually decompose.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px)✔ ¬(∀y)(Qy∨¬Qy✔ | 1¬∧D |
| 3 | (∃x)¬(Px→Px)✔ (∃y)¬(Qy∨¬Qy)✔ | 2¬∀D |
| 4 | ¬(Pa→Pa) ¬(Qa∨¬Qa) | 3∃D |
[We now have a negated conditional and a negated disjunction. They are on different branches. We begin with the left one.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px)✔ ¬(∀y)(Qy∨¬Qy✔ | 1¬∧D |
| 3 | (∃x)¬(Px→Px)✔ (∃y)¬(Qy∨¬Qy)✔ | 2¬∀D |
| 4 | ¬(Pa→Pa) ¬(Qa∨¬Qa) | 3∃D |
| 5 | Pa | | 4¬→D |
| 6 | ¬Pa | | 4¬→D |
[This creates a contradiction, so we mark the branch as closed. We then decompose the right branch. It will produce a double negation that we will also decompose.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px)✔ ¬(∀y)(Qy∨¬Qy✔ | 1¬∧D |
| 3 | (∃x)¬(Px→Px)✔ (∃y)¬(Qy∨¬Qy)✔ | 2¬∀D |
| 4 | ¬(Pa→Pa) ¬(Qa∨¬Qa) | 3∃D |
| 5 | Pa | | 4¬→D |
| 6 | ¬Pa | X | | 4¬→D |
| 7 | ¬Qa | 4¬∨D |
| 8 | ¬¬Qa | 4¬∨D |
| 9 | Qa | 8¬¬D |
[We can again see the contradiction, so we mark it as closed too.]
| 1 | ¬[(∀x)(Px→Px)∧(∀y)(Qy∨¬Qy)]✔ / \ | P |
| 2 | ¬(∀x)(Px→Px)✔ ¬(∀y)(Qy∨¬Qy✔ | 1¬∧D |
| 3 | (∃x)¬(Px→Px)✔ (∃y)¬(Qy∨¬Qy)✔ | 2¬∀D |
| 4 | ¬(Pa→Pa) ¬(Qa∨¬Qa) | 3∃D |
| 5 | Pa | | 4¬→D |
| 6 | ¬Pa | X | | 4¬→D |
| 7 | ¬Qa | 4¬∨D |
| 8 | ¬¬Qa | 4¬∨D |
| 9 | Qa X | 8¬¬D |
(Agler 307)
So since the original formula’s negation creates a closed tree, it is a tautology (Agler 307).
7.3.4 Logical Equivalence
We next will test to see if pairs of propositions in RL are logically equivalent. Agler defines equivalence in this way.
Equivalence: A pair of propositions ‘P’ and ‘Q’ is shown by the truth-tree method to be equivalent if and only if the tree of the stack of ‘¬(P↔Q)’ determines a closed tree; that is, all branches for ‘¬(P↔Q)’ close.(Agler 310)
Agler begins with the example of the pair of expressions:
(∀x)Px¬(∃x)Px(Agler 310)
We next need to place them into a negated biconditional and test to see if it creates a closed tree, in which case it will be equivalent.
| 1 | ¬[(∀x)Px↔¬(∃x)Px] | P |
[We next decompose the negated biconditional.]
| 1 | ¬[(∀x)Px↔¬(∃x)Px]✔ / \ | P |
| 2 | (∀x)Px ¬(∀x)Px | 1¬↔D |
| 3 | ¬¬(∃x)Px ¬(∃x)Px | 1¬↔D |
[Now, since we only need to find one open branch to determine that the tree is not closed, we might only need to do the left branch for example. So let us first do the double negation.]
| 1 | ¬[(∀x)Px↔¬(∃x)Px]✔ / \ | P |
| 2 | (∀x)Px ¬(∀x)Px | 1¬↔D |
| 3 | ¬¬(∃x)Px✔ ¬(∃x)Px | 1¬↔D |
| 4 | (∃x)Px | 3¬¬D |
[With the choice of the universally and existentially quantified formulas, we should do the existential one first.]
| 1 | ¬[(∀x)Px↔¬(∃x)Px]✔ / \ | P |
| 2 | (∀x)Px ¬(∀x)Px | 1¬↔D |
| 3 | ¬¬(∃x)Px✔ ¬(∃x)Px | 1¬↔D |
| 4 | (∃x)Px✔ | 3¬¬D |
| 5 | Pa | 4∃D |
[Now we can do the universal.]
| 1 | ¬[(∀x)Px↔¬(∃x)Px]✔ / \ | P |
| 2 | (∀x)Px ¬(∀x)Px | 1¬↔D |
| 3 | ¬¬(∃x)Px✔ ¬(∃x)Px | 1¬↔D |
| 4 | (∃x)Px✔ | 3¬¬D |
| 5 | Pa | 4∃D |
| 6 | Pa | 2∀D |
[We have nothing left to decompose, since we have already done all the constants in the branch for the universal quantifier. Thus this is an open branch.]
| 1 | ¬[(∀x)Px↔¬(∃x)Px]✔ / \ | P |
| 2 | (∀x)Px ¬(∀x)Px | 1¬↔D |
| 3 | ¬¬(∃x)Px✔ ¬(∃x)Px | 1¬↔D |
| 4 | (∃x)Px✔ | 3¬¬D |
| 5 | Pa | 4∃D |
| 6 | Pa O | 2∀D |
[One completed open branch is enough to determine that it is not a closed tree. So] the original are thus not equivalent.
Agler then gives a more complicated example.
(∀x)¬(Px∨Gx)(∀y)(¬Py∧¬Gy)(Agler 310)
[So first we set them up as a negated biconditional.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]} | P |
[Now we decompose the biconditional.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx) (∀y)(¬Px∧¬Gx) | 1¬↔D |
[We will continue work on the left branch. We should first decompose the negated quantifier in line 3.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx) | | 3¬∀D |
[This gives us an existential quantifier, which should come next.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga) | | 4∃D |
[We now have the universally quantified expression and the negated conjunction. At this point I am not sure if it matters which we do next. Agler does the negated conjunction.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa ¬¬Ga | | 5¬∧D |
[We should next decompose these double negations.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
[What is left in this branch is the universally quantified expression in line 2.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga) ¬(Pa∨Ga) | | 2∀D |
[This new proposition we can decompose into ¬Pa and ¬Ga. Agler will decompose just the first part for the first branch and stop, because it creates a contradiction. For the second branch, he will decompose both parts, because it is not until we get to the second part of the decomposition that we find a contradiction. We then mark the self-contradiction branches with an X to note that it is closed.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga) ¬(Pa∨Ga) | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
[This leaves the right branch. We should decompose the negated quantifier first.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga)✔ ¬(Pa∨Ga)✔ | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
| 11 | (∃x)¬¬(Px∨Gx) | 2¬∀D |
[This we can existentially decompose (and skip the double negation decomposition).]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga)✔ ¬(Pa∨Ga)✔ | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
| 11 | (∃x)¬¬(Px∨Gx)✔ | 2¬∀D |
| 12 | Pa∨Ga | 11∃D |
[We will now decompose this expression.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga)✔ ¬(Pa∨Ga)✔ | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
| 11 | (∃x)¬¬(Px∨Gx)✔ | 2¬∀D |
| 12 | Pa∨Ga✔ / \ | 11∃D |
| 13 | Pa Ga | 12∨D |
[Now we can decompose the universally quantified expression from line 3.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga)✔ ¬(Pa∨Ga)✔ | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
| 11 | (∃x)¬¬(Px∨Gx)✔ | 2¬∀D |
| 12 | Pa∨Ga✔ / \ | 11∃D |
| 13 | Pa Ga | 12∨D |
| 14 | ¬Pa∧¬Ga ¬Pa∧¬Ga | 3∀D |
[In order to find contradictions, we only need to decompose one part of line 14 for each branch.]
| 1 | ¬{[(∀x)¬(Px∨Gx)]↔[(∀y)(¬Py∧¬Gy)]}✔ / \ | P |
| 2 | (∀x)¬(Px∨Gx) ¬(∀x)¬(Px∨Gx) | 1¬↔D |
| 3 | ¬(∀y)(¬Px∧¬Gx)✔ (∀y)(¬Px∧¬Gx) | 1¬↔D |
| 4 | (∃y)¬(¬Px∧¬Gx)✔ | | 3¬∀D |
| 5 | ¬(¬Pa∧¬Ga)✔ | / \ | | 4∃D |
| 6 | ¬¬Pa✔ ¬¬Ga✔ | | 5¬∧D |
| 7 | Pa Ga | | 6¬¬D |
| 8 | ¬(Pa∨Ga)✔ ¬(Pa∨Ga)✔ | | 2∀D |
| 9 | ¬Pa ¬Pa | | 8¬∨D |
| 10 | X ¬Ga | X | | 8¬∨D |
| 11 | (∃x)¬¬(Px∨Gx)✔ | 2¬∀D |
| 12 | Pa∨Ga✔ / \ | 11∃D |
| 13 | Pa Ga | 12∨D |
| 14 | ¬Pa∧¬Ga ¬Pa∧¬Ga | 3∀D |
| 15 | ¬Pa ¬Ga X X | 14∧D |
(Agler 310-311)
So since this is a closed tree, that means the original two propositions are equivalent (Agler 311).
7.3.5 Validity
We will now test to see if arguments are valid. Agler defines validity and invalidity this way.
Validity: An argument ‘P, Q, R, ..., Y ⊢ Z’ is shown by the truth-tree method to be valid in RL if and only if the stack ‘P,’ ‘Q,’ ‘R,’ ..., ‘Y,’ ‘¬Z’ determines a closed tree.Invalidity: An argument ‘P, Q, R, ..., Y ⊢ Z’ is shown by the truth-tree method to be invalid in RL if and only if the stack ‘P,’ ‘Q,’ ‘R,’ ..., ‘Y,’ ‘¬Z’ has at least one completed open branch. (Agler 314)
Agler first shows how we do this with a simple argument, namely:
(∀x)Px, Pa ⊢ Pa
(Agler 314)
| 1 | (∀x)Px | P |
| 2 | ¬Pa | P |
(Agler 314, with the ‘x’ changed to an ‘a’ in line 2)
There is really only one option now for decomposition, namely, line 1.
| 1 | (∀x)Px | P |
| 2 | ¬Pa | P |
| 3 | Pa X | 1∀D |
(Agler 314)
Because this tree is closed, that means there is no way that the premises can be true and the conclusion false. [For, we showed that there is no possible interpretation to make the premises true and the negation of the conclusion true.] Thus this argument is valid.
Agler then gives a more complicated example.
(∀x)(Px→Qx), (∃y)(Py) ⊢ (∃x)(Px→Qx)(Agler 314)
Let us set it up.
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py) | P |
| 3 | ¬(∃x)(Px→Qx) | P |
[Of our options, we should do either the second or the third line. The second one is simpler, so perhaps that is why we begin with it.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx) | P |
| 4 | Pa | 2∃D |
[Now we can decompose the negated quantifier.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx)✔ | P |
| 4 | Pa | 2∃D |
| 5 | (∀x)¬(Px→Qx) | 3¬∃D |
[Since we now have two universal quantifiers, it is perhaps arbitrary which to do next. We begin with the first one.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx)✔ | P |
| 4 | Pa | 2∃D |
| 5 | (∀x)¬(Px→Qx) | 3¬∃D |
| 6 | Pa→Qa | 1∀D |
[And we will now do the other universal quantifier, perhaps because it is a stacking rule but our other option is a branching one.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx)✔ | P |
| 4 | Pa | 2∃D |
| 5 | (∀x)¬(Px→Qx) | 3¬∃D |
| 6 | Pa→Qa | 1∀D |
| 7 | ¬(Pa→Qa) | 5∀D |
[We would decompose line 7 with a stacking rule, so let us do that one next.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx)✔ | P |
| 4 | Pa | 2∃D |
| 5 | (∀x)¬(Px→Qx) | 3¬∃D |
| 6 | Pa→Qa | 1∀D |
| 7 | ¬(Pa→Qa)✔ | 5∀D |
| 8 | Pa | 7¬→D |
| 9 | ¬Qa | 7¬→D |
[And finally we can decompose the remaining conditional, which will give us two closed branches and thus a closed tree.]
| 1 | (∀x)(Px→Qx) | P |
| 2 | (∃y)(Py)✔ | P |
| 3 | ¬(∃x)(Px→Qx)✔ | P |
| 4 | Pa | 2∃D |
| 5 | (∀x)¬(Px→Qx) | 3¬∃D |
| 6 | Pa→Qa | 1∀D |
| 7 | ¬(Pa→Qa)✔ | 5∀D |
| 8 | Pa | 7¬→D |
| 9 | ¬Qa / \ | 7¬→D |
| 10 | ¬Pa Qa X X | 6→D |
(Agler 314-315)
So because the tree is closed, the argument is valid.
Agler then has us consider this argument.
Pa∧Qb, (∀x)(∀y)[Px→(Qy→Rx)] ⊢ Ra(Agler 315)
To test for its validity, we need to see if the following propositions are consistent.
{Pa∧Qb, (∀x)(∀y)[Px→(Qy→Rx)], ¬Ra}(Agler 315)
[Let us set it up.]
| 1 | Pa∧Qb | P |
| 2 | (∀x)(∀y)[Px→(Qy→Rx)] | P |
| 3 | ¬Ra | P |
[We have two options. I am not sure if it is arbitrary or not, but we begin first with line 1.]
| 1 | Pa∧Qb✔ | P |
| 2 | (∀x)(∀y)[Px→(Qy→Rx)] | P |
| 3 | ¬Ra | P |
| 4 | Pa | 1∧D |
| 5 | Qb | 1∧D |
[As we can see, we now have two constants in the branch so far. Our next option is to decompose the main operator of line 2, which is the first universal quantifier. And we will need to do it for the two constants.]
| 1 | Pa∧Qb✔ | P |
| 2 | (∀x)(∀y)[Px→(Qy→Rx)] | P |
| 3 | ¬Ra | P |
| 4 | Pa | 1∧D |
| 5 | Qb | 1∧D |
| 6 | (∀y)[Pa→(Qy→Ra)] | 2∀D |
| 7 | (∀y)[Pb→(Qy→Rb)] | 2∀D |
[Now we have the two universal quantifiers. We will again have to do each one for both constants.]
| 1 | Pa∧Qb✔ | P |
| 2 | (∀x)(∀y)[Px→(Qy→Rx)] | P |
| 3 | ¬Ra | P |
| 4 | Pa | 1∧D |
| 5 | Qb | 1∧D |
| 6 | (∀y)[Pa→(Qy→Ra)] | 2∀D |
| 7 | (∀y)[Pb→(Qy→Rb)] | 2∀D |
| 8 | Pa→(Qa→Ra) | 6∀D |
| 9 | Pa→(Qb→Ra) | 6∀D |
| 10 | Pb→(Qa→Rb) | 7∀D |
| 11 | Pb→(Qb→Rb) | 7∀D |
[Now we have four options that are each nested conditionals. We will want to close off branches. If we do either lines 8 or 9, we will have ¬Pa, which will give us a closed branch. The question then is, which of these two is better. If we later decompose the internal conditional of line 8, then we will get ¬Qa, which does not close the branch, and Ra, which does. However, if we do the one from line 9, then we will ¬Qb, which closes a branch, and Ra, which also does. So we do 9 and eventually close all branches.]
| 1 | Pa∧Qb✔ | P |
| 2 | (∀x)(∀y)[Px→(Qy→Rx)] | P |
| 3 | ¬Ra | P |
| 4 | Pa | 1∧D |
| 5 | Qb | 1∧D |
| 6 | (∀y)[Pa→(Qy→Ra)] | 2∀D |
| 7 | (∀y)[Pb→(Qy→Rb)] | 2∀D |
| 8 | Pa→(Qa→Ra) | 6∀D |
| 9 | Pa→(Qb→Ra)✔ | 6∀D |
| 10 | Pb→(Qa→Rb) | 7∀D |
| 11 | Pb→(Qb→Rb) / \ | 7∀D |
| 12 | ¬Pa Qb→Ra✔ X / \ | 9→D |
| 13 | ¬Qb Ra X X | 12→D |
(Agler 315)
Since all branches close, that means the set of propositions
Pa∧Qb, (∀x)(∀y)[Px→(Qy→Rx)], ¬Rais inconsistent. That furthermore means that the argument
(Agler 316)
Pa∧Qb, (∀x)(∀y)[Px→(Qy→Rx)] ⊢ Ra
is valid.
Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.
Some changes to the book quotations may have been made, as based on: http://markdfisher.com/wp-content/uploads/2014/02/PHIL_012_ONLINE_SYLLABUS_SP14-3-1.pdf .
.
No comments:
Post a Comment