Suppes (9.8) Introduction to Logic, “Venn Diagrams”, summary

by Corry Shores

[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Patrick Suppes, entry directory]
[Suppes’ Introduction to Logic, entry directory]

[The following is summary. My commentary is in brackets. Boldface is mine. I apologize in advance for any distracting typos.]

 

Summary of

 

Patrick Suppes

 

Introduction to Logic

 

Ch. 9 Sets

 

§9.8 Venn Diagrams

 

 

Brief summary:
We may depict sets and their relations and properties using Venn diagrams. A rectangle signifies the domain of individuals. Inside it we draw circles to represent sets. These circles may overlap to designate intersections. We can shade regions to mean there are no members there. An x-shaped cross signifies that a particular region has at least one member. However, if an x-shaped cross is linked by a line to another cross, that means at least one of the crosses’ connected regions is non-empty (and thus some, but not all, of the linked cross regions can be empty, despite them having a cross marking). When statements about the set-relations are logically consistent, then a crossed region that is also shaded as empty is really empty, because the shading dominates the crossing. However, if the statements are inconsistent, then this inconsistency might be apparent in a dually shaded and crossed region that should still retain its member despite the shading. Syllogistic inferences can be tested by constructing a diagram for the premises, and then we see if the conclusion is compatible with what is depicted.

 

 

Summary

 

 

To better grasp the relations between sets, it can help to depict them using diagrams.

one draws a rectangle to represent the domain of individuals, and then draws circles, or other figures, inside the rectangle – thinking of the points inside the various figures as corresponding to the members of the sets being represented by the figures.
(195)

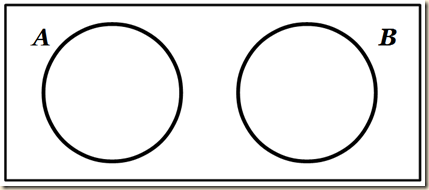
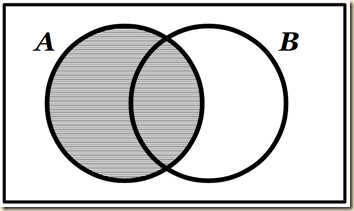
Suppes has us consider that we have two mutually exclusive sets, A and B [see section 9.5. He notated it there as: A ∩ B = Λ]. We could depict the situation in the following way.

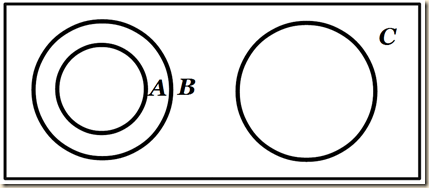
Suppose now that A ⊆ B. Then our diagram could look like this.

We can also say for this situation that “All A are B” (196).

 

Now suppose that we have sets A, B, and C. Here, “A ⊆ B (all A are B) and B ∩ C = Λ, (i.e., no B are C)” (196).

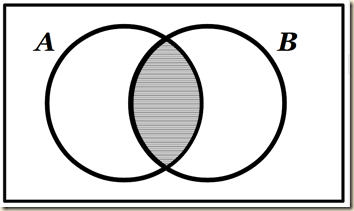
[The diagram makes something visually obvious that symbolically may be less so. From A ⊆ B (all A are B) and B ∩ C = Λ, (i.e., no B are C) we can deduce that nothing in A is in C. But when we see the diagram, we do not even need to think too much about it. The image says it all.] From this diagram we can clearly see that A ∩ C = Λ or “no A are C” (196).

 

Suppes will use horizontal shading [or we might say, horizontal hatch markings] to represent an empty set (197). So below would be the diagram for A ∩ B = Λ.

[Recall again the prior diagram for A ⊆ B.

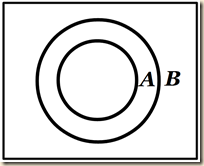
We see that all of A is enclosed by B. This also means that no part of A is found outside of B, which is also obvious in the image. Now that we have this additional visual indicator for the empty set, we can instead show some of A lying outside of B, but shade that exterior part to indicate that there are no members of A lying outside of B. Thus in a different way we can represent the same set relation A ⊆ B.] The diagram below would represent the situation where A ⊆ B; “for to say that A is a subset of B means that no part of A lies outside B” (197).

Suppes then notes another way that the diagrams make certain properties of the sets more immediately obvious. For example, consider two parts of a situation: A ∩ B = Λ and A ⊆ B. From this it might not be apparent that A is the empty set, but by combining the prior two diagrams, we can see that it is [for, A is entirely shaded as empty] (197).

 

Another visual indicator for a different property are linked crosses for non-emptiness. So suppose that some A are B, or symbolically, that: A ∩ B ≠ Λ. We would depict this by making an x-shaped cross-mark in the common region between A and B to indicate that it is not empty.

[We will now have another idea that we will need to represent. Let us make an example first to illustrate. (Forgive me, however, if I confuse things too much.) So let us consider we have garments that can have three types of patterns or any of their combinations: (a) upslope blue lines, (b) vertical red lines, and (c) downslope green lines. To see what their combinations would look like, we might add their imagery to the diagram. But this is just to serve as a visual reminder of how things of one sort can be combined or not combined with things of other sorts. We should not here confuse these markings with emptiness (which we instead are indicating with horizontal black lines).

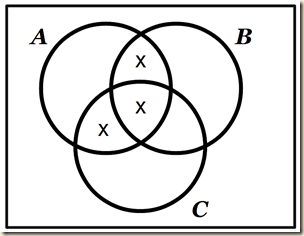
We still need to use the conventions of x-crosses and linking. Now suppose our graph looked like this:

Again, here the hatch marks do not indicate anything about membership. They just remind us of the garment patterns. So this chart I think is saying that we know there is at least one garment that is both A and B, at least one that is both A and C, and at least one that is in combination A, B, and C. Since there is no empty set indication in the other regions, I am supposing this means that there could be members of other sorts, but we do not say either way. I am not sure however. But we do here say that there are in fact members in the marked regions. Now, suppose we have a box of garments we have not opened. We are told that there is at least one garment in it. There might be more. Let us just suppose there are numerous ones. Of these that we are speaking of (of the ones that should be represented with an x-cross), we know that all of them have red stripes in combination with other stripes (there maybe are ones other than these combination ones, but I am not sure). Yet we do not know everything about these ones in question. So it could be that all of them are both red and blue. It could be that all of them are both red and green. It could be that all of them are red green and blue. Or it could be some variety of these types. But as you notice, it would be misleading to use the diagram above for this new situation. That diagram asserted that in fact there were at least one of each combination. But now, we only know that at least one of the three is there, although the others may be there too. So for this we introduce a new marking. We will connect the x-crosses with a line. And whenever x-crosses are connected with lines, that means that among all those in that connected group, at least one of them is there.

In other words, we know that there are members in at least one of the sets, but we do not specify which ones.] Now suppose we wanted to depict A ∩ (B ∪ C) ≠ Λ. [This says the following. Suppose there are three sets, A, B, and C. First consider if we unite B and C, and thus now we are thinking about all the members of B and C in total, regardless of whether or not those members are found inside or outside the other set in this pair. Now, consider all those from set A that are found in that combination of B and C. The claim then is that there is at least one member of A that is also in B or C . Thus] we interpret this as “some A are either B or C” (198).

But what if we omit the lines connecting the x-crosses?

This [as we noted in our comments above] means that there is a member of the intersection of A and B, in exclusion of C. This can be notated:

(A ∩ B) ~ C ≠ Λ

[meaning, the set of members that are in the intersection of A and B but that are not in C is non-empty; or, there is at least one member in the part of the diagram where A and B overlap but without overlapping with C (see the top ‘x’ region)] It also tells us that there is a member in the intersection of A and C, in exclusion of B. This can be written:

(A ∩ C) ~ B ≠ Λ

[meaning, the set of members that are in the intersection of A and C that are not in the group B is non-empty; or, there is at least one member in the part of the diagram where A and C overlap but without overlapping with B (see the bottom ‘x’ region).] And lastly it also means that there is a member in the intersection of A, B, and C.

A ∩ (B ∩  C) ≠ Λ

[meaning, the set of members that are in A’s intersection with the intersection of B and C is non-empty; or, there is at least one member in the part of the diagram where A, B, and C overlap (see the middle ‘x’ region).] (198)

 

Suppes then diagrams the following situation:

A ∪ B ≠ Λ        (Something is either A or B)
A ∪ ~C ≠ Λ     (Something is either A or not C)
(Suppes 198)

 

We will now examine a situation where shading will dominate an x-cross. Consider this situation:

A ∩ C ≠ Λ     (Some A are C)
C ⊆ B               (All C are B)

We would diagram it like this:

C ⊆ B tells us to shade in all those parts of C that are not in B. But A ∩  C ≠ Λ tells us to put x-crosses in the parts where A and C overlap. Now, since the shading coincides with one of the x-crosses, it dominates that cross, and we can conclude that there are no members of that intersection (199). [I am not sure about this conclusion, but perhaps he is saying that we can remove the other x-cross and the connecting line.

]

 

Suppes then explains that there is an instance where we would not want to say that the shading dominates the crossing, namely, when the conditions are inconsistent. Consider this situation:

A ⊆ C
A ∩ C = Λ  
A ∩ B ≠ Λ 

A ⊆ C tells us to shade in all parts of A that are not in C. But A ∩  C = Λ  tells us to shade in all the parts that both A and C share. So now all of A is shaded, including all places where it intersects with B. So when it says A ∩ B ≠ Λ, we have a contradiction. It tells us to put linked crosses in the regions where A and B intersect. This means at least one of them should have a member, and thus it should not be that both are shaded. But as we can see, they are in fact both shaded.

When every cross in a linkage of crosses is “covered” by shading we must conclude that the diagram is inconsistent rather than that the linked regions are completely empty, for a linkage of crosses means that at least one of the regions linked is non-empty. We may in fact use these circumstances to investigate by use of Venn diagrams the consistency of a set of conditions imposed on sets.
(200)

 

We will now see how we can use the diagrams to visually determine when syllogistic inferences are valid. So consider this syllogism:

(1) No B are C
(2) All A are B
(3) Therefore no Aare C
(Suppes 200)

“No B are C” tells us to shade in all the parts where B and C overlap. And “All A are B” tells us to shade in all the parts of A which do not overlap with B. We then check if  (theref0re) “no Aare C”. As we can see from there diagram, the two premises caused us to shade in the areas where A and C overlap (201). Suppes ends by making a few useful notes regarding the use of Venn diagrams for assessing the validity of syllogisms.

All other valid syllogisms may be tested in the same way, but there is no need to restrict the use of Venn diagrams to testing the validity of those arguments which have the classical syllogistic form. Venn diagrams may be used to represent any argument which does not involve more than three sets. Moreover, by a careful use of ellipses in place of circles relations among four sets can be represented diagrammatically, but relations among five or more sets can often not be represented by any simple diagrammatic device.
(201)

 

 

 

 

Suppes, Patrick. Introduction to Logic. New York: Van Nostrand Reinhold / Litton Educational, 1957.

 

 

 

.