by Corry Shores
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Set Theory, entry directory]
[Wikibooks: Set Theory, entry directory]
[My commentary is in brackets.]
Summary of
Wikibooks: Set Theory
Sets
Subsets, power sets, set operations
Brief summary:
The members of a set are in total and in every possible combination subsets of the set of which they are a part. A ⊆ B means that A is a subset of B. If B has members not in its subset A, then A is a proper subset: A ⊂ B. If we list every possible combination of a set’s items into subset grouping, we have given that set’s power set, denoted with a script ‘P’. The union of two sets is the set of all their combined members, denoted by ∪ . The intersection of two sets is the set of all items they have in common, denoted with ∩ . The relative complement of one set in relation to a second one is all the members in the first that are not in the second, denoted with \ . The absolute complement are all the members in the universe that are not in some particular set, denoted with U\ .
Summary
Subsets
[The idea with subsets seems to be that whether or not we had in mind to group the terms within a set into smaller sets, they can already be said to form such groups. So the mutual inclusion of items in a set is automatically their internal subgrouping into subsets of that set. At any rate,] if all the members of one set are found in another set, then the first is a subset of the second, and we use this symbol: ⊆ . There are two things to keep in mind about subsets. One is that the empty set is a subset of all other sets [but from what has been said here, I really do not know why.] The second is that every set is a member of itself [I am not sure why here either, but notationally speaking I can imagine adding another set of curly braces around whatever is enclosed by the main ones.] [We can imagine one set having the same exact same contents as another, and then, given what we just said about self-inclusion, we can say that the one set is a subset of the other. However, we might also want to reserve a concept for subsets that are not identical to the sets of which they are a part. These we call proper subsets, and we use this symbol: ⊂ .]
A set S is a subset of set A if every member of S is a member of A. We use the horseshoe notation to indicate subsets. The expression
says that {1, 2} is a subset of {1, 2, 3}. The empty set is a subset of every set. Every set is a subset of itself. A proper subset of A is a subset of A that is not identical with A. The expression
says that {1, 2} is a proper subset of {1, 2, 3}.
[Wikibooks]
Powersets
[The next concept, powersets, seems to build from the idea that the members of a set are by default already forming their own subsets. In fact, they form every possible combination. If we listed them all explicitly, we would have the powerset of a set.]
A power set of a set is the set of all its subsets. A script 'P' is used for the power set. Note that the empty set and the set itself are members of the power set.

[Wikibooks, image modified to fit]
Union
[We might want to know what happens when you combine all the members of one set with all those of another. Here we use this symbol: ∪ . Recall from the prior section that the members are unique, so it is superfluous to repeat any. This means that if after combining two sets you have duplicate terms, you can just omit them from the list. ]
The union of two sets A and B, written A ∪ B, is the set that contains all the members of A and all the members of B (and nothing else). That is,
As an example,
Intersection
[We might instead want to know what members are shared in common between two sets, if in fact they share any to begin with. Here we use this symbol: ∩ .]
The intersection of two sets A and B, written A ∩ B, is the set that contains everything that is a member of both A and B (and nothing else). That is,
As an example,
Two sets are disjoint if their intersection is empty. That is, if A and B are disjoint sets,
Relative complement
[Above, we were interested in what is common between sets. But what about what is not shared? We might want to know what members are in one set but not in another. This is the relative complement, denoted with a \ .]
The relative complement of A and B, denoted B \ A (sometimes B − A), is the set containing all the members of B that are not members of A. That is,
As an example,
Absolute complement
[I am not certain with this concept. But it seems to be the following. Previously with the relative complement, we compared two specific sets, looking for what one has which the other lacks. We might also broaden our scope to consider all things and all sets we are taking into consideration in that case (our “universe”). And we can ask, what elements in the universe are not found in some particular set? This seems to be what the absolute complement is, which is notated with the \ again, but with a U for universe coming first. Other notation is also mentioned.]
If we define a universe, or a set containing all of the elements we wish to consider, then we can discuss the absolute complement of a set. For a universe U, define the absolute complement of a subset A of U to be
The absolute complement of A is denoted by
,
or
(according to the ISO 31-11 standard) if U is fixed.
[Wikibooks]
Source (of text and images):
Wikibooks. “Set Theory/Sets.” <https://en.wikibooks.org/wiki/Set_Theory>
(Accessed 25-03-2016)
.















































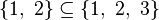
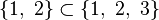






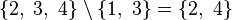

No comments:
Post a Comment