by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Graham Priest, entry directory]
[Graham Priest’s One, entry directory]
[The following is summary. All boldface, underlying and bracketed commentary are my own.]
Summary of
Graham Priest
One:
Being an Investigation into the Unity of Reality and of its Parts, including the Singular Object which is Nothingness
Preface
P.5 Paraconsistency
Brief Summary:
We are accustomed to using what is called ‘classical logic’ in our normal inferential thinking. But it has a bizarre rule, called ‘explosion’. If you have a self-contradiction, then you can infer from it any other proposition. Yet, there is a non-classical logic called paraconsistent logic, and it says that self-contradictions do not necessarily imply any other proposition. Dialetheism holds that not only is this so, but we can say that some self-contradictions are true.
Summary
Priest has elsewhere gone into great detail in working out his ideas in dialetheic and paraconsistent logic, but he will here give a brief account of his philosophical presuppositions.
Dialetheism says that some contradictions are true. This holds not just in language but in the real world.
Dialetheism is a metaphysical view: that some contradictions are true. That is, where ¬ is negation, there are sentences, propositions (or whatever one takes truth-bearers to be), A, such that A and ¬A are both true. Given that A is false iff (if and only if) its negation is true, this is to say that there are some As which are both true and false. (Priest, xviii)
[A proposition might imply another one. This would be a logical consequence of it. We need now understand what a ‘relation of logical consequence is’, and for this I can only offer my best guesswork. The premises relate to the consequence. This relation can have certain properties. One possible property is that if there is a self-contradiction in the premises, then any additional proposition can be found in the consequence, no matter how unrelated to the self-contradiction. This property of the consequence relation is called ‘explosion’ (or perhaps ‘explosivity’). This is also called ‘triviality’, perhaps because one set of premises can entail all other possible ones, making all trivial (meaning that no differences make any difference, because all terms have the same value. Below this is shown in diagrams. We might think of triviality as all sentences being in the ‘true’ group, meaning that there are no differences in value between them, no differences that make a difference.) But, if a self-contradiction in the premises does not have explosivity as a logical consequence, then the property of the logical consequence relation is ‘paraconsistency’. To avoid triviality, dialetheists must hold that the true contradictions are paraconsistent in their consequences.]
Paraconsistency is a property of a relation of logical consequence. Explosion is the property of such a relation according to which any contradiction implies anything. That is, a relation of logical consequence, ⊢, is explosive iff for all A and B, {A,¬A} ⊢ B. A consequence relation is paraconsistent iff it is not explosive. There is, of course, a connection between dialetheism and paraconsistency. In particular, if one is a dialetheist, one had better hold that the appropriate logical consequence relation is paraconsistent, on pain of accepting everything: triviality. (xviii)
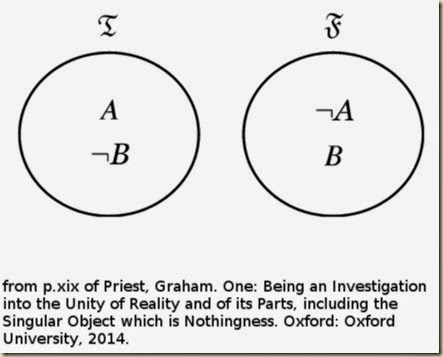
[We may have learned logic as a system of mechanics governing inference, which lies underneath the language that we use. The science of this mechanics has advanced quite far, and it can take a very mathematical form. Now imagine. We strip away all meanings. We build a machine with symbols. These symbols begin with no meaning and no governed relations. We can then arbitrarily shape the mechanical properties of how the symbols convert and generate one another. This is a sort of calculus. We might have this series of symbols: ¬(P∧Q), and we can say it can arbitrarily be replaced by this series (¬P)∧(¬Q). All this is just mechanics. Recall Gregory Bateson’s claim that “Information consists of differences that make a difference.” (Bateson, Gregory. Mind and Nature: A Necessary Unity. London: Wildwood House, 1979, p.110a). When we view the sequences in this purely mechanical way, we have differences (one formulation is not another), and those differences generate other differences. However, none of those differences ‘make a difference’ in the sense of having difference in value, power, importance, interest, and so on. One way we can make such differences is assigning an interpretation value to the sequences. We can assign certain formulas to one class, call it ℑ, and certain others to another class, call it ℱ. This gives the formulations another level of meaning. But they would take on even more significance if it made a difference to us which category they were in. If we translate those in the ℑ category as true and those in the ℱ as false, then these differences can make a difference to we who are making use of these machines to make sense of our world. There is a tradition of designating true and false assignments that has been accepted as orthodox for some time now. It is ‘classical logic’. It says that if we assign a formulation the value of ℑ (in other words, if it is true), then that formulation with the ¬ symbol in front of it (its negation) is assigned the value of ℱ (in other words, the negation is false).]
Those who have never met dialetheism and paraconsistency before may well be puzzled by the views. Let me do at least a little to unpuzzle. In classical logic, any situation (interpretation) partitions all truth-bearers into two classes: the true (ℑ) and the false (ℱ). The two classes are mutually exclusive and exhaustive. Given that negation is a functor which toggles a sentence between truth and falsity, a sentence is in ℑ iff its negation is in ℱ, and vice versa. Thus, we have the following:
(xix)
One way of defining validity is to say that “if there is no situation where all the premises are true and the conclusion is not true,” then the inference is valid. [Now recall that a consequence relation is explosive if a self-contradiction in the premises entails any other formulation. We formulated it as {A,¬A} ⊢ B. If it is valid, then we cannot have {A,¬A} ⊢ ¬B. But if we look at our circles, we never have A, ¬A as true, so explosion is valid in this model.]
A standard definition of validity is to the effect that an inference is valid if there is no situation where all the premises are true and the conclusion is not true. Given the above set-up, there is no situation where, for any A, both A and ¬A are true. A fortiori, there is no situation where A and ¬A are true, and B is not—whatever B you choose. That is, Explosion is valid. (xix)
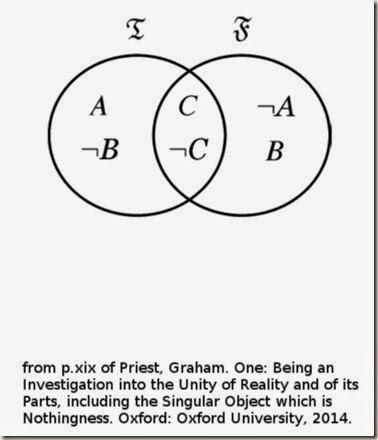
[Now suppose we use a different way to assign the truth and falsity values, and we allow there to be cases where we allow a particular formulation and its negation to have both ℑ and ℱ assignments. We may think of this situation as the two groups overlapping in this certain case. Suppose we place C and its negation in such a special circumstance, but not any other formulation. This means that both C and its negation can be found together on the true side, but B’s negation is still exclusively on the true side. So we do not have both a self-contradiction and B being true, and thus explosion is not valid here.]
But now suppose that ℑ and ℱ may actually overlap in some situations. Given that negation works in the same way, it follows that if C is in the overlap, so is its negation. Thus, we have the following:
For a situation of this kind, both C and ¬C are true (and false as well; but at least true). But B is false only (not true). Given exactly the same definition of validity as before, it follows that Explosion is not valid. (xix)
Although there is more that can be said about paraconsistent logic, this is what is most fundamental to it. Most of it is like first-order logic, but an exception should be noted.
Most of the other machinery of a formal logic may be taken to behave as it does in classical logic, though the following is worth noting. In first-order logic, a predicate has an extension—the set of things of which it is true—and an anti-extension—the set of things of which it is false. In classical logic, the anti-extension need not be mentioned explicitly, since it is simply the complement of the extension.However, in a paraconsistent logic, the extension of a predicate does not determine the anti-extension. It therefore needs a separate specification. (xx)
Priest, Graham. One: Being an Investigation into the Unity of Reality and of its Parts, including the Singular Object which is Nothingness. Oxford: Oxford University, 2014.