The Glue of Chaos: Isomorphism, Diagram, and Analogy in the Semiology of Charles Sanders Peirce

by Corry Shores 
[Search Blog Here. Index-tags are found on the bottom of the left column.

[Central Entry Directory] 
[Logic and Semantics, Entry Directory] 
[C.S. Peirce, entry directory]
[Deleuze on Bacon Entry Directory]

The Glue of Chaos

Isomorphism, Diagram, and Analogy
in the Semiology of Charles Sanders Peirce

What does isomorphism got to do with you?

We find a certain coherence in our world, and as well there is a coherence in how we represent our world. We might observe some event, like a ball smashing a window. There is a sort of causal coherence to that event. Then we might formulate a sentence to describe the event to someone else. If the description is accurate, then the description will have a logical coherence to it as well. What is remarkable is that we can move from the parts of the world to the parts of our representations. This is only possible if we designate one-to-one relations between the parts of one domain with those of the other, even though these parts do not always resemble one another, as in the case of symbolic language. This one-to-one relation between the parts of the different domains is an isomorphic relation. It is isomorphism that allows us to place our world in a symbolic medium.

Brief Summary

Peirce distinguishes three types of signs: icons, indices, and symbols. Icons resemble their referent; indices are causally imprinted by their referent, and symbols stand for their referent on account of some convention or habit of relating the two. A diagram can be an icon, because the parts of the diagram resemble the parts of the thing it represents. Symbols are made of icons, because a symbol evokes in us a mental image that resembles the symbol's referent. Because there is a one-to-one correspondence between the symbol and its proper mental icon, we can say that symbols are made of icons on account of isomorphism.

Relevance to Deleuze
[Under ongoing revision]

Deleuze ties together the concepts of diagram, analogy, icon, symbol, isomorphism, and digital coding in the "Analogy" chapter of his Francis Bacon: The Logic of Sensation. His purpose is to explain his highly complex and original concept: the aesthetic analogy. The concept of isomorphism will allow him to characterize an analogous relation between an original and a production, which are related by a medium that does not resemble either one. This medium is the chance influence that deforms by means of modulation the original's parts. In this way it produces something with different parts with new relations. The parts now are incompatible. But the forces that glued the original's parts coherently together now force together the changed parts in an incoherent way. The device which causes this modulatory deformation is what Deleuze calls a diagram. He distinguishes it from Peirce's diagram, which produces similar relations of parts rather than dissimilar ones. Deleuze also speaks of how the symbol for Peirce is made of icons. The importance here is that the new modulated parts might have vague sensible resemblances to the original, although the original and the modulated part refer to different objects. So the new modulated part iconically refers to the original, even though the meanings they symbolize are incompatible. The importance of this is that the iconic relation between the original and the modulation preserves the forces that organized the original's parts, and it is these contracting forces which are pushing together the incompatible parts of the modulation. This will make more sense when we discuss Deleuze's aesthetic analogy in a forthcoming entry.



The following summary is from:

C.S. Peirce

Philosophical Writings of Peirce

Ch7. Logic as Semiotic: The Theory of Signs

I. What is a Sign? Three Divisions of Logic

Peirce will expound his theory of signs. His synonym for sign is representamen (99a). So whenever he uses the term representamen, we may take it to mean 'sign.'

Let's look at the core components involved in his theory. Besides the sign itself is the person who is being aware of its meaning. Another component is what the sign stands for. So he defines a sign:

A sign, or representamen, is something which stands to somebody for something in some respect or capacity. (99a)

The sign 'addresses' the person involved, and creates in her mind an equivalent or more developed sign. This sign created in the addressed person's mind Peirce calls the interpretant of the first sign.

The sign stands for something else, and this other thing Peirce calls the sign's object.

Peirce also discusses the idea that is evoked by signs. The idea is just a notion that we can communicate to others and that we can conceive more than once, with the idea being mostly the same each time. This idea is the ground for the sign or representamen. This is because the sign does not entirely stand in the place of its object, but more importantly it refers to the idea involved in its meaning. (99a.b)

Thus Peirce divides the sign or representamen into three general elements: the ground [the idea related to the object], the object itself, and the interpretant [the sign in the mind of the person whom the sign addresses].

There is then a triadic relation in Peirce's theory of signs.
The (1) sign relates to (2) an object in such a way that it may evoke (3) in the person's mind the sign, the interpretant related to the first sign.

Three Trichotomies of Signs
ii

Peirce distinguishes three types of signs: icon, index, and symbol. [He will clarify in the following section]

1) Icon.
An icon refers to its object solely on account of certain characteristics that it bears. It is 'like' the thing it is a sign for. (102bc)

2) Index
An index refers to an object on account of its actually being affected by that object. The modification that the object causes to the index is what allows it to denote that object. For this reason, it may bear a similar quality to the object, and hence in a way involves a peculiar sort of icon. (102c)

3) Symbol
A symbol denotes an object on account of some law. Usually this is a law of association of general ideas. This association causes the symbol to be taken as referring to its associated object. (102d)

3. Icon, Index, and Symbol

a. Synopsis

1) Icon
Icons possess a character that makes it signify something, even if that thing does not exist. For example, a pencil-line can be an icon for a geometrical line, even though it is only like a geometrical line on account of similar characteristics, and even though geometrical lines cannot exist in actuality. (104bc)

2) Index
An index has some trait caused by the object, and this trait is what allows the index to denote that object. We may think of things that have causally affected one another, leaving their imprint, but without there being some person having a sign in their minds for this object leaving the imprint. In other words, we can remove the interpretant [idea in addressed person's mind] and still have and index, but if we remove the object [and its imprint], the index is no longer significant. Peirce's example is a piece of moulding that was shot, producing a bullet-hole. The hole would be there, regardless of whether there is someone to attribute this hole to a bullet-shot. However, were there no hole, then the moulding cannot possible refer indexically to some bullet-shot. (104bc)

3) Symbol
A symbol is a speech utterance whose signification results from it being understood to have that signification. Hence what happens is that when someone sees a symbol, she then conceives another sign in her mind that stands for the object represented both by the physical sign and the mental one. So a symbol needs an interpretant [mental sign] in order to be significant.

b. Icon

Icon's have a representative quality whose likeness to the object allows it to iconically refer to that object. In a sense, anything can substitute something else that it is like.

Peirce also calls an iconic representamen a hypoicon. A painting, taken just in terms of the resemblances to objects that it produces, is an example of a hypoicon. (105b)

There are three types of hypoicons: images, diagrams, and metaphors. An image bears simple similar qualities to its object. A diagram bears relations in its own parts that are analogous to the relations in the object's parts. A metaphor represents something by means of a parallelism in something else. (105bc)

According to Peirce, we have only one way to directly communicate an idea, and that is by means of an icon. Indirect ways must be grounded on icons. (105c)

Pictures are icons. So too are diagrams, even though there is not really a sensuous resemblance between the diagram and its object. Instead, in diagrams there is merely an analogy between the relations of the diagram's parts to the object's parts. (105d) "it is only in respect to the relations of their parts that their likeness consists." (107a)

c. Index

An index is "in dynamical (including spatial) connection both with the individual object, on the one hand, and with the senses or memory of the person for whom it serves as a sign, on the other hand" (107d).

Peirce offers some examples.

A rap on the door is an index. Anything which focuses the attention is an index. Anything which startles us is an index, in so far as it marks the junction between two portions of experience. Thus a tremendous thunderbolt indicates that something considerable happened, though we may not know precisely what the event was.
. . . A low barometer with a moist air is an index of rain; that is we suppose that the forces of nature establish a probable connection between the low barometer with moist air and coming rain. A weathercock is an index of the direction of the wind; because in the first place it really takes the self-same direction as the wind, so that there is a real connection between them, and in the second place we are so constituted that when we see a weathercock pointing in certain direction it draws our attention to that direction, and when we see the weathercock veering with the wind, we are forced by the law of mind to think that direction is connected with the wind. The pole star is an index, or pointing finger, to show us which way is north. A spirit-level, or a plumb bob, is an index of the vertical direction. (109a.c)

d. Symbol

A symbol is a sign that represents an object on account of some rule or habit determining what mental sign will be evoked in the mind of the person addressed by the symbol. (113a)

Peirce explains here how a symbol can be made of icons (as well as indices). He seems to say that the symbol needs to somehow evoke mental icons whose character refers us to the represented object.

A man walking with a child points his arm up into the air and says, "There is a balloon." The pointing arm is an essential part of the symbol without which the latter would convey no information. But if the child asks, "What is a balloon," and the man replies, "It is something like a great big soap bubble," he makes the image a part of the symbol. (112bc)

He further explains how symbols refer to mental icons.

A Symbol is a sign naturally fit to declare that the set of objects | which is denoted by whatever set of indices may be in certain ways attached to it is represented by an icon associated with it. To show what this complicated definition means, let us take as an example of a symbol the word "loveth." Associated with this word is an idea, which is the mental icon of one person loving another. Now we are to understand that "loveth" occurs in a sentence; for what it may mean by itself, if it means anything, is not the question. Let the sentence, then, be "Ezekiel loveth Huldah." Ezekiel and Huldah must, then, be or contain indices; for without indices it is impossible to designate what one is talking about. Any mere description would leave it uncertain whether they were not mere characters in a ballad; but whether they be so or not, indices can designate them. Now the effect of the word "loveth" is that the pair of objects denoted by the pair of indices Ezekiel and Huldah is represented by the icon, or the image we have in our minds of a lover and his beloved. (112-113)

The following is from:

The Essential Peirce: Selected Philosophical Writings

Of reasoning in general

In another text he offers another example of how symbols refer to mental icons whose character points to that object that the icon resembles.

in the proposition, "A sells B to C for the price D," A, B, C, D form a set of four indices. The symbol "___ sells ___ to ___ for the price ___" refers to a mental icon, or idea, of the act of sale, and declares that this image represents the set A, B, C, D, | considered as attached to that icon, A as seller, C as buyer, B as object sold, and D as price. [20-21, boldface mine]

So we see that symbols are composed of icons. Now we need to understand why Deleuze says that this composition is based on "phenomena of isomorphism." We will look more closely at this passage:

In his great semiological theory, Peirce first defined icons by similitude, and symbols by a conventional rule. But he acknowledged that conventional symbols are composed of icons (by virtue of phenomena of isomorphism), and that pure icons range far beyond qualitative similitude, and consist of "diagrams." [ft.5: "In his theory of the sign, Peirce attaches great importance to the analogical function and to the notion of the diagram. Nonetheless, he reduces the diagram to a similitude of relations." (citations), p.137b] (Deleuze 81c)

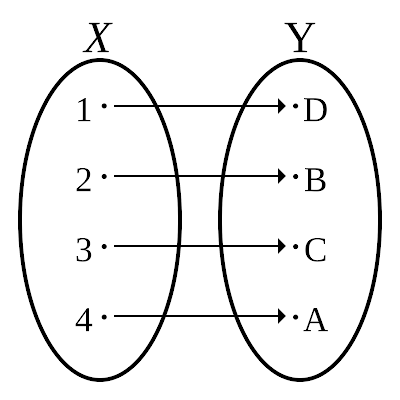
We will first look at what makes an isomorphism, first in a somewhat technical manner. Consider two sets:

Set X's members: 1, 2, 3, 4
Set Y's members: A, B, C, D

We will then say that there is a function involved. Recall Edwards' & Penney's "Function Machine":

A function is like a machine that takes-in one value and gives-out another. In the case of our isomorphism, we will say that there is a function that takes-in members of the first set, and gives-out members of the other set. If we take-in '1' and give out 'D', we would represent this as:

f(1) = D.

Let's make the other assignments.

f(1) = D
f(2) = B
f(3) = C
f(4) = A

Wikipedia nicely represents this pictorially as:

We see that the assignments are arbitrary. We also notice that there is a one-to-one correspondence between the elements of the sets (Landsberg 58). This is like how the symbols we use are arbitrary, but refer according to conventions or habits. The convention or habit of association, then, is the function that makes the two domains isomorphic to one another. So we call that thing which is like a great soap bubble a "balloon", because that is the convention. And as we noted before, for Peirce, the symbol evokes a mental icon for the object. So there is something like a 'function' which takes in the symbol, and gives out the mental icon. It is perhaps in this way that Deleuze means symbols are composed of icons by virtue of phenomena of isomorphism. The symbols would be meaningless if they did not isomorphically relate to mental icons that directly refer to objects similar to them.

This then will help us understand how Deleuze means "analogy by isomorphism," when talking about digital coding. Let's take binary as an example of digital coding. There are two abstract elements, the one and the zero. [Perhaps they are abstract, because these numerals refer to discrete machine states, and thus the coding is something like an abstraction for the machine state; that is, its switches or whatever else are either in one or another position.]

Deleuze writes that we may "do at least three things with a code. One can make an intrinsic combination of abstract elements." (Deleuze 80c) So with our 1 and our 0, we may for example combine them to obtain:

0100100001100101011011000110110001101111

Deleuze continues, "One can also make a combination which will yield a 'message' or a 'narrative', that is, which will have an isomorphic relation to a referential set." (Deleuze 80c) So let's take our binary string as an example. We can for example break it into 8-bit parts.

01001000 01100101 01101100 01101100 01101111

Then, we can establish something like an isomorphic function to tell us how to convert these symbol-groups into letters. [Using the ASCII convention, we might say]

f(01001000) = H
f(01100101) = e
f(01101100) = l
f(01101100) = l
f(01101111) = o

[This example is taken from: docdroppers.org] In this way, our string "0100100001100101011011000110110001101111" can be converted into "Hello," on account of the isomorphism of the sets. In fact, the original string was composed intentionally for this translation. Deleuze then writes, "Finally, one can code the extrinsic elements in such a way that they would be reproduced in an autonomous manner by the intrinsic elements of the code (in portraits produced by a computer, for instance, and in every instance where one could speak of "making a shorthand of figuration.)" (Deleuze 80c) The intrinsic elements seem in our case to be the 8-bit arrangements. And the extrinsic elements would be the letters. Computer software, running on the basis of binary codes, can automatically convert these binary sequences to the letters on our screens, just like how they convert the binary data of an image file to a picture we can see. So first we begin with "Hello" or some image. That is then converted to binary numerical codes for the letters or the homogenized square regions (pixels) of the image. The computer than by means of its own processes reproduces that original word or image, all mediated by the numerical code.

Notice how there is no resemblance between the letter formation and its isomorphic binary equivalent. And likewise with Deleuze's example, there is no resemblance between an image file's binary sequence and the image the software autonomously reproduces on our screen. Nonetheless, it is by means of this automatic reproduction that the resemblance to the original is produced, all through a medium, binary code, that bears no resemblance to the thing it codes and reproduces. But the thing it reproduces is similar to the thing that was originally rendered into code, so in a way the product is analogous to the original. Deleuze writes: "It seems, then, that a digital code covers certain forms of similitude or analogy: analogy by isomorphism, or analogy by produced resemblance" (80d).


Finally let's make one remark regarding Deleuze's observation that for Peirce, diagrams can be icons. This is because the relations of the diagram resemble the relations of the object it represents. Deleuze contrasts his own notion of diagram with Peirce's. We will see in a forthcoming entry that for Deleuze, a diagram regards something with relations that do not resemble the original's relations.

Deleuze, Gilles. Francis Bacon: The Logic of Sensation. Transl. Daniel W. Smith. London/New York: Continuum, 2003.

Edwards & Penney. Calculus. New Jersey: Prentice Hall, 2002, p.2a-3c.

Landsberg, Marge E. Syntactic iconicity and linguistic freezes: The human dimension. Berlin/New York: Mouton de Gruyter/Walter de Gruyter, 1995.
Possible preview at:
http://books.google.com/books?id=xgXh7rAz0E8C&dq=Marge+E.+Landsberg&source=gbs_navlinks_s

Peirce, C.S. The Essential Peirce: Selected Philosophical Writings. Vol 2 (1893-1913). Bloomington Indiana: Indiana University Press, 1998.
Possible preview at:
http://books.google.be/books?id=grYAoECfZtIC&dq=Nathan+Houser&hl=en&source=gbs_navlinks_s

Peirce, C.S. Philosophical Writings of Peirce. New York: Dover Publications, Inc, 1955.



Internet sources:

Hello example:
http://www.docdroppers.org/wiki/index.php?title=Learning_Binary

ASCII alphabet code:
http://www.tekmom.com/buzzwords/binaryalphabet.html

Isomorphism graphic:
http://en.wikipedia.org/wiki/Bijection