[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Deleuze Entry Directory]
[Spinoza Entry Directory]
[Deleuze on Bacon Entry Directory]
[Let me please sincerely thank the sources of the images used in this entry:
wiki
Fayetteville State University Department of Mathematics and Computer Science
physics.cornel
mediacollege.com
jimloy.com
Paul Falstad
acoustics.salford.ac.uk
Note: some images are uncredited, because I obtained them very long ago. If they are recognized, please let me know so I may obtain permissions or be asked to take them down.
corrymshores@gmail.com
Thanks!]
What does Spinozistic rhythm got to do with you?
Our lives are filled with our relations with the world and other people. We are continually responding and reacting to what goes on around us, and these events might change us profoundly. And often we need to change ourselves even if slightly to adjust to the conditions of each situation. Our changing relations have a sort of rhythm to them. How well we learn to dance with this rhythm determines how well we will thrive in life.
Brief Summary:
Bodies are made fundamentally of differences, and bodies combine with each other to the degree that their differences maintain in their coexistence. Something's own inner differences is a matter of the differential relations between the speeds of its parts. The sum total of these differential relations determines the power of the body. This power is its capacity to affect other bodies and to withstand the affections of other bodies. When two bodies encounter, they affect one another. Each one sends a shock-wave of differential variation through the other. It survives if its parts maintain differentially relating with one another despite the new differences that were introduced. And if the colliding bodies themselves continue differentially relating together, they form a third body. The way that bodies relate is a matter of their speeds and slownesses differentially relating to one another, and this manner of relating Deleuze calls rhythm.
Points Relative to Deleuze:
In his Francis Bacon: The Logic of Sensation, Deleuze writes of the rhythms involved when Bacon's paintings give us sensations. We might understand this rhythm as our body's differential interaction with the variations in the painting.
Spinoza's Rhythm
We will look at Deleuze's use of the term 'rythme' in a couple of his Spinoza courses. When we find him using the term in Francis Bacon: The Logic of Sensation, he seems not to not always mean it in the conventional sense. He refers us to Messiaen's and Boulez' meaning of the term, which we find to be something more like continual variation in the patterns of temporal divisions. Yet there still might be more to understand. Let's look at rhythm and Spinoza.
We first will need to review some calculus ideas Deleuze teaches us. We first think of a curve as a point in motion. Imagine that we are spinning around a ball tied to a string. It makes a circle. If we cut the string while it is spinning, it does not fly off in a spiral. Rather, it shoots-off in a straight line. This is because it is constantly tending to move at a ninety degree angle to the string.
Now consider just the circle that the ball's motion makes. Curves like on a circle can have something called a tangent line. It is angled against the curve so that it just touches in that one place. It also depicts the direction that the curve is tending at that place, too. So the ball was tending to fly outward at a ninety degree angle from the string. Likewise, on a circle, the tangent line lies at a ninety degree angle to the radius. It depicts for us the conflict of powers (centrifugal and centripetal) that cause it to be aimed in its particular direction. Consider more complex curves.
We can sort of feel the direction the points are headed. But there is a more precise way of determining which way the point is tending to fly-off at a certain place along the curve. Consider first when we examine a region of the curving variation, to determine the average change. Imagine we are representing the motion of a ball, distance per time.
The diagonal line tells us where the curve was generally tending during that region of variation. But it does not tell us where it was tending at any point. In other words, it does not give us what speed the object was tending at a particular place and time in its motion. To do so, we use a technique that diminishes both the change-in-time and the change-in-distance down to an infinitely small magnitude. Each value by itself no longer has a magnitude in comparison to the finite magnitude it began as. However, these two infinitely small magnitudes can still maintain their ratio value to one another. And this value in a sense has a quantity. Deleuze explains this by referring us to Leibniz' doubled triangle demonstration. Two right triangles, whose diagonal (hypotenuse) line is mutually constructed, maintain the same proportions as one is reduced while the other increases. So as the lines of the small one diminish to the infinitely small (but not yet completely zero), they still maintain the same ratio as the lines of the larger triangle. Hence we can still conceive of a finite value holding between two non-finite (infinitesimal) magnitudes.
(Image my own, made with OpenOffice Draw and GIMP)

(Animation above is my own, made with Open Office Draw and Unfreeze.)
(Animation above is my own, made with Open Office Draw and Unfreeze.)
So watch as we reduce the two magnitudes of the axis. See how it alters the angle of the diagonal, until it seems to depict the way the curve is tending at the given point.
This animation shows how the tangent is angled at each place along the curve, and we can see how it depicts the way the curve is tending at each point. [When it turns black, it hits points of inflection. Some day we will turn to this concept that Deleuze discusses in The Fold.]
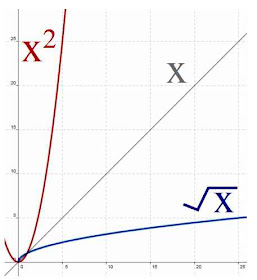
So we are deriving the tangent on a curve. Our curves can be described by functions. What we find is that in order to find the derivative, we need the x and the y values to be at different powers, that is, having different exponents. Deleuze refers us to a concept of depotentialization, which he very well might have drawn from Hegel's calculus writings in the Science of Logic (especially§§569-570). Consider the graph below. If we just have y = x, then we just have a straight line, and not a curve.
But when we have y = x squared or y = the square root of x, then we have curves. What seems to allow for the function's line to curve is that there is a difference of power between them. In the case of y = x, they both tug on each other about the same amount throughout their variations. But in y = x squared, it is as though y pulls more-and-more on x as x increases, which is why the curve rapidly tilts upwards. So we might think of y having an increasing power, or having power of a higher order. For each standard unit of increase of y, it has an increased influence on x, and the magnitude of that influence itself increases with each unit. Deleuze refers to this as an acceleration. We will need to use this metaphorically to extract an idea we later use: we can only find the power relations on a curve if our line is curved, and we can only have a curved line if x and y have different powers in relation to one another.
Spinoza's Body Differentials
So we turn now to Deleuze's Spinozistic theory of affection and the body. At any moment, we are affected more-or-less by something [see Deleuze Cours Vincennes 20-01-1981]. This gives us more-or-less power to survive, and it indicates our capacity to endure such influences. As well, it tells us our power to influence other things. Our level of affection is always in continuous variation, like a curve. So at any moment, there is an instantaneous affection. It is the degree to which our level of affection is trying to change. It is the intensity of the change, stripped from the actual transition, and this transition requires duration to express itself fully. So if someone poisons us with arsenic, we lose power to survive, act, withstand influences and cause influences. Too much, and we die.
Deleuze further incorporates the differential calculus to explain this in physical terms. He finds implicit in Spinoza's thinking the idea of "simple bodies" [see Spinoza's Letter 32, Deleuze's Cours Vincennes 10-03-1981, and Deleuze's Expressionism in Philosophy, Chapter 13.] Spinoza discusses the composition and coherent relations of parts in the world in his Letter 32 to Oldenburg. Spinoza says that parts cohere when "the laws or nature of one part adapts itself to the laws or nature of another part in such wise that there is the least possible opposition between them" (Spinoza Letters 192d). So he is taking into consideration
things as parts of a whole to the extent that their natures adapt themselves to one another so that they are in the closest possible agreement. In so far as they are different from one another, to that extent each one forms in our mind a separate idea and is therefore considered as a whole, not a part. (Spinoza Letters 192-193)Spinoza offers an example "the motions of particles of lymph, chyle, etc.," which he regards as the parts of the blood. The particles
adapt themselves to one another in accordance with size and shape so as to be fully in agreement with one another and to form all together one single fluid, to that extent only are the chyle, lymph, etc. regarded as parts of the blood. But in so far as we conceive the particles of lymph as different from the particles of chyle in respect of shape and motion, to that extent we regard them each as a whole, not a part. (193a)We will find that Deleuze will emphasize not so much the principle that allows the parts to accord with one another, but rather the difference which makes them different and thus relatable to begin with. We will first note how Deleuze conceives these parts which differentially relate to one another. Bodies, including our own, extend in space. This means they are made of smaller extending parts. We can keep dividing parts and only find more extensive pieces. But if we were to infinitely divide an extending part, we would have something that no longer extends, because it is infinitely small. So blood is made of lymph and chyle. We can divide chyle up into infinitely small pieces. They do not actually exist, because they are no longer extending bodies. But they are virtually there. Consider how we looked at an infinitely small part of time and an infinitely small part of space when finding the instantaneous velocity. We cannot have speed without an extent of time or space, because there is no motion. However, the instantaneous velocity is real. So it is real but not actual. This is Deleuze's virtual. We will try to apply this to extending bodies. There are not really infinitely small bodies making up our larger bodies. However, they are there virtually, and they can be explicated by means of our differential analysis. Deleuze will explain more.
So we consider that we may find some infinitely small reduction of a part of chyle. It is not really there, but when we place that tiny value in relation to another one, we can find the differential value holding between them. So note first the following. Our blood has a certain quantity of power (and so does the arsenic). What does this value come from? Deleuze says that the particles relate according to differences in speed and slowness. It could be that an infinitely small part of chyle moves at a different speed than an infinitely small part of lymph. I would suggest another conception. We might say that the lymph and chyle affect one another, but the one being of a greater power, like the x squared. So the difference in power would be like different speeds, one pulling harder and faster than another, causing the acceleration of the line's change in our graphs. Let's try this interpretation. So chyle and lymph are made of infinite sets of infinitely small parts. There is a power struggle between the sets, and this produces a value, indicating the blood's power. So if there are violent forces of variation in a body, it will be more powerful. It will be able to undergo the influence of very strong other differential values. So consider then if arsenic enters our blood. Our blood already has a differential value, so too does the arsenic. The bodies of our blood and those of the arsenic collide. If we can somehow be beings with arsenic in our blood, and still survive, then we are incorporating more differential variation within us. We evidently are strong, because it can survive even when poisoned. But if our blood decomposes, causing our body to decompose with it, then the arsenic decreased our power. This is power based on constitutive difference, on variation.
When the arsenic enters our blood, it will differentially relate to the blood's parts, and in that way affect the blood's relations. This will affect the way the other parts of our bodies differentially relate, in a chain reaction ending in the decomposition of our bodies. So the arsenic caused waves of affection to flow through our bodies, and this happens on the basis of a differential encounter. Later when discussing Deleuze's aesthetic affection, we will return to this notion.
One Body, One Blood?
The reason we consider blood to be one thing with parts is only because the parts have differentially related. If they assimilated, there would be no composition of parts, just a heterogeneous composition, whose parts are only spatially different. In other words, consider when the arsenic enters the blood. The two differentially relate in such a way that blood decomposes. We might rather say that it deforms. The blood is already a deformation of lymph and chyle. So when lymph bodies meet chyle bodies, one has more power than the other, but the two benefit from each other's differences and continue relating until new bodies like arsenic disrupt the differential relations. So blood is one body not in the sense that it consists of assimilated parts, quite the opposite: we call it a body because conditions allow its parts to persist in their differentially affecting one another, until something causes alteration.
Bodies of Rhythm
Let's now clarify then Deleuze's Spinozistic concept of body, by turning to his Spinoza: Practical Philosophy. In Spinoza: Practical Philosophy, he will associate two somewhat parallel distinctions:
Kinetic / Dynamic
Longitude / Latitude
When we define a body kinetically, we regard their being infinitely small parts that differentially relate to one another in terms of differences in speeds and slownesses.
How does Spinoza define a body? A body, or whatever kind, is defined by Spinoza in two simultaneous ways. In the first place, a body, however small it may be, is composed of an infinite number of particles; it is the relations of motion and rest, of speed and slownesses between particles, that define a body, the individuality of a body. (Practical Philosophy, 123a)He writes in a footnote that these particles whose speeds and slownesses differentially relate are 'simplest bodies,' which are the infinitely small divisions of extensive bodies [for more on simplest bodies as infinitely small divisions of extensive bodies, see Cours Vincennes 10-03-1981, and Deleuze's Expressionism in Philosophy, Chapter 13.] This kinetic dimension is also what Deleuze calls the longitude of the body:
We call longitude of a body the set of relations of speed and slowness, of motion and rest, between particles that compose it from this point of view, that is, between unformed elements. (Practical Philosophy 127c) [ft.3: Cf. what Spinoza calls "the simplest bodies." They have neither number nor form nor figure, but are infinitely small and always exist as infinities. The only bodies having a form are the composite bodies, to which the simple bodies belong according to a particular relation. (Practical Philosophy 127d)]
We might find ourselves interested at times in form and at other times in the changes that forms undergo. Yet both the form of something and its mutations are both grounded on the differential relations of speeds and slownesses of the parts. Blood is composed by the differential relations between infinitely small parts of chyle's speed and infinitely small parts of lymph's speed (that is, all the one's tendencies-toward-change and all the other's). The sum integrated total of all these differential relations, at a given time, between the infinitely small parts under differential relations between the sets, might be the form. The mutation of forms might then come from the differential relations between the elements of one moment with those of another moment. This would look at how one body relates to itself over time as it continually alters. So while we might find form and alteration to be interesting, Deleuze says:
The important thing is to understand life, each living individuality, not as a form, or a development of form, but as a complex relation between differential velocities, between deceleration and accelerations of particles. (Practical Philosophy 123bc)
That fact that things change, or that they 'become' can be quite interesting. But what might interest us more are what underlies those becomings, which are the differential relations. These perhaps are more matters of logic than metaphysics. They are the source of the power that secondarily gets expressed as change.
Deleuze also defines these differential relations of speeds and slownesses in musical terms, and we will return to this metaphor of music later.
Now, however, we define a body dynamically when we take into account the way it affects other bodies and is capable itself of withstanding affections.
Secondly, a body affects other bodies, or is affected by other bodies; it is this capacity for affecting and being affected that also defines a body in its individuality. (Practical Philosophy 123a)Deleuze points-out that we will understand the things in our world differently when we comprehend them in terms of their capacity for giving and enduring affections instead of in terms of their formal relations. He has us consider the way we understand plow horses, racing horses, and oxen. Normally we would think that the horses are more akin to each other than is either horse to the ox. But let's consider these animals in terms of their affective capacities.
Take any animal and make a list of affects, in any order. Children know how to do this: Little Hans, in the case reported by Freud, makes a list of affects of a draft horse pulling a cart in a city (to be proud, to have blinders, to go fast, to pull a heavy load, to collapse, to be whipped, to kick up a racket, etc.) (Practical Philosophy 124a)A draft horse has much the same capabilities as an ox. A race horse might struggle too much under the burden, respond wickedly to the whip, fear the situation rather than respond with pride in its abilities. But even capabilities might vary according to circumstances. If we were meditating in the dark, and someone turns on the light, this will dazzle our eyes and decrease our powers. But if we were looking for our glasses in the dark and then someone turns on the light, it increases our powers. These increases and decreases are always instantaneous and infinitesimal. [Deleuze Cours Vincennes 20-01-1981].
Deleuze also refers to the dynamic sense of body as latitude.
We call latitude the set of affects that occupy a body at each moment, that is, the intensive states of an anonymous force (force for existing, capacity for | being affected). (Practical Philosophy 127-128)
We turn now to Deleuze's using the metaphor of music to illustrate the kinetic view of the body:
The important thing is to understand life, each living individuality, not as a form, or a development of form, but as a complex relation between differential velocities, between deceleration and accelerations of particles. A composition of speeds and slownesses on a plane of immanence. In the same way, a musical form will depend on a complex relation between speeds and slownesses of sound particles. It is not just a matter of music but how to live: it is by speed and slowness that one slips in among things, that one connects with something else. (Practical Philosophy 123c)Deleuze will develop this music metaphor further. He will also use the example of a wave. So let's take a look at what he might mean by taking a look at what could be the differential relations in sound waves.
When waves intersect, the can either add or subtract from one another, depending on how the waves are lining up.
So you can see the different possibilities.
So when two waves intersect, they push and pull on each other, and thereby create a co-composed deformation. Even a harmonic combination is still a deformation of the original waves:
We might see this better with a three dimensional animation of waves differentially deforming one another. [This animation comes from one of Paul Falstad's absolutely amazing simulators].
Now consider also this animation from the University of Salford, showing how the overtones of a string combine. These are additional smaller waves that accompany all real waves in the world around us. [See this entry on Pythagoras for a detailed explanation.]
So we see that these wave-combinations, even when harmonic, produce deformed waves. But such deformations perhaps would only come about if the parts were differentially related, each one communicating its differences to the other.
Deleuze uses the musical metaphor to describe Spinoza's vision of the world's composition. Bodies are made of these differential relations between the infinitely small parts of infinite sets. The values of those relations determine the combined differential body's affective power. Again, this affective power is its capacity to sustain a differential relation to another body without disintegrating apart or becoming assimilated into the other body. We saw in the three-dimensional animation how the smaller wave can still be seen in the larger one, and the larger one still discerned despite the smaller one's cutting through it.
But even for the more complex wave forms, like the guitar string one above, we may still extract the component overtone values by means of Fourier analysis [discussed in this entry]. This means that no matter how much the component waves seem to have been swallowed-up and assimilated, they are still implied in the composite wave. So if we could see the sound waves in the air while a symphony plays, we would notice the effects of all the differential variations affecting one another as they come into contact. In other words, we would see the composition in the air as a network of differential relations that are the affections between different speeds and slownesses.
we are concerned [...] with a symphony of Nature, the composition of a world that is increasingly wide and intense. In what order and in what manner will the powers, speeds, and slownesses be composed? A plane of musical composition, a plane of Nature, insofar as the latter is the fullest and most intense Individual, with parts that vary in an infinity of ways. [126d]In his seminars on Spinoza, Deleuze better explains the differential and compositional relations of affective speed. He begins with the idea of the simplest bodies, the infinitely small parts of a body [The following is from Cours 12 du 17/03/81]. They have no internal composition, because they are like the infinitely small values of vanishing terms. So they can only have external relations. When another body impacts us, that is, when our differentially related parts shockingly impact the other body's parts, both sets will differentially relate, causing changes in the relations of our internal parts, like a wave moving through us, changing all the other waves as it passes. We might know then how we were changed by that external wave. This is the first kind of knowledge. But we might also something about our own differential relations and how they differentially relate to other differential relations. Deleuze gives the example of swimming through a wave. The second kind of knowledge is 'know-how', which involves knowing how our body differentially relates to others and also our knowing how to change our own inner differential relations so that we sustain our differential relation with the thing we encounter.
When we jump into the water to swim, our simplest bodies and the wave's simplest bodies shockingly contact one another and send through each other waves of affective variations. This impact registers on our body, and the imprint is like the first kind of knowledge. This is the effect of the shock. But that does not mean we know anything about our own relations or the wave's relations.
But if we adjust our body so that we swim through the wave, then we have more than just a knowledge of the immediate shocking impact that the wave has on us. Deleuze calls it a sense of rhythm. This is a knowledge of how our differential relations differentially relate to other differential relations.
Alors, au contraire je sais nager, ça veut pas dire forcément que j’ai une connaissance mathématique ou physique, scientifique du mouvement de la vague, ça veut dire que j’ai un savoir faire. Un savoir faire étonnant, c’est à dire qui une espèce de sens du rythme. La rythmicité. Qu’est-ce que ça veut dire le rythme ? Ca veut dire que mes rapports caractéristiques je sais les composer directement avec les rapports de la vague. ça se passe plus entre la vague et moi, c’est à dire ça se passe plus entre les parties extensives, les parties mouillées de la vague, et les parties de mon corps, ça se passe entre les rapports. Les rapports qui composent la vague, bon, les rapports qui composent mon corps, et mon habileté, lorsque je sais nager, à présenter mon corps sous des rapports qui se composent directement avec les rapports de la vague. Alors c’est : Je plonge au bon moment, je ressort au bon moment, j’évite la vague qui approche ou au contraire je m’en sers, etc. Tout cet art de la composition des rapports (Cours 12 du 17/03/81)Recall also our reasoning for using the term 'ratio' instead of 'relation' when speaking of the differential relations of speeds and slowness between parts. This was because the speeds or slowness (or better, their instantaneous tendencies toward speed or slowness) are quantitative, so their relation could be one of a ratio. This also could help explain why our knowing how the speeds and slownesses relate is a matter of a sense of rhythm. We normally think of rhythms as a repeating pattern per some amount of time. And we might say that a rhythm has a certain relative speed to it, depending on how it divides temporal portions. But in this Deleuzean sense, rhythm is the way speeds differentially relate. When we jump in the water, knowing how to maintain ourselves within the water, despite our continual differences with the wave, is a sense of rhythm. So rhythm in this sense is something immediate, and it is not so much like a pattern repeating through time. Specifically, rhythm is the way the different speeds of bodies affect themselves and one another in response to each other.
Deleuze uses both the swimming example and a dancing example in another seminar. He says when we encounter the wave or enter the dance floor, we are living in the rhythm of our interaction, where we are continually anticipating how the wave or dance-body will affect us, and then also we adjust ourselves so that we survive through it. He notes that those who do not know how to dance might anger everyone by dancing however they can so to disrupt the overall flow. (Cours - 03/02/81 - 2) This would be a case where one body fails to cause itself to self-differentiate in such a way that it sustains its differential relation with another body. The bad dancer causes the dance to break-down, and hence there becomes no point for him to be dancing anymore. And he himself, by angering everyone, has lowered his own social powers of affection.
Deleuze also uses the metaphor of musical instruments playing together to illustrate the rhythmic combination of a third body. He says that rhythm is something like the shared interaction at the boundary of two meeting bodies. Rhythm is not so much to be found in the violin or the piano alone, rather rhythm is to be found in violin responding and reacting to the piano all while the piano at the same time responds and reacts to the violin. This is sort of like them dancing. The third body then is the musical work that their shared rhythmic interaction produces. [Le rythme c’est une notion commune à deux bords au moins. Le rythme il est fondamentalement commun à au moins deux bords. Il n’y a pas le rythme du violon, il y a le rythme du violon qui répond au piano et le rythme du piano qui répond au violon. Ça c’est une notion commune à ce moment là. Vous savez la notion commune de deux corps, le corps du piano et le corps du violon, sous l’aspect, sous tel ou tel aspect, c’est-à-dire, sous l’aspect du rapport... du rapport qui constituera telle œuvre musicale et qui forme le troisième corps.] (Cours 31/03/81 - 14_- 2)
Sources:
Deleuze, Gilles. Spinoza: Practical Philosophy. Transl. Robert Hurely. San Francisco: City Lights Books, 1988.
Deleuze's Spinoza Course Classes:
Cours 20/01/1981
webdeleuze.com
French and English
Cours 03/02/81 - 2
http://www2.univ-paris8.fr/deleuze/article.php3?id_article=221
Cours 10/03/1981
(webdeleuze.com)
French and English
Cours 17/03/81
http://www2.univ-paris8.fr/deleuze/article.php3?id_article=151
Cours 31/03/81 - 14_- 2
http://www2.univ-paris8.fr/deleuze/article.php3?id_article=46
Cours 02/12/1980 - 1
http://www2.univ-paris8.fr/deleuze/article.php3?id_article=91
http://www.webdeleuze.com/php/texte.php?cle=209&groupe=Spinoza&langue=1
Spinoza. The Letters. Transl Samuel Shirley. Cambridge: Hackett Publishing Company, Inc., 1995.
Image and animation sources.
Derivative animation
http://faculty.uncfsu.edu/msiddiqu/Maple_Animations.htm
(Thanks Fayetteville State University Department of Mathematics and Computer Science)
Wikipedia sliding tangent
http://en.wikipedia.org/wiki/File:Graph_of_sliding_derivative_line.gif
(Thanks wiki)
3-D Wave animation made using:
http://www.falstad.com/mathphysics.html
(Thanks Paul Falstad)
Phase sound wave image:
http://www.mediacollege.com/audio/images/wave-interaction.gif
(Thanks mediacollege.com)
Combining wave animation:
http://pages.physics.cornell.edu/courses/p101/6/demo2.html
(Thanks physics.cornel)
String combination animation from:
http://www.acoustics.salford.ac.uk/feschools/waves/string.htm
(Thanks acoustics.salford.ac.uk)
Harmonic wave combination image:
http://www.jimloy.com/physics/harmony.htm
(Thanks jimloy.com)











No comments:
Post a Comment