Iser (§3) “The Reading Process: A Phenomenological Approach,” part III, summary

 

by Corry Shores

[Search Blog Here. Index tabs are found at the bottom of the left column.]

[Central Entry Director]
[Literature, Drama, and Poetry, Entry Directory]
[Literary Criticism, Entry Directory]
[Wolfgang Iser, Entry Directory]
[Iser, “The Reading Process,” Entry Directory]

 

[The following is summary. All boldface and parenthetical commentary are my own.]

 

 

Wolfgang Iser

 

“The Reading Process: A Phenomenological Approach”

 

III

 

 

Brief summary:

The literary work of art is not merely an objective given. It arises through the imaginative interaction of the reader with the raw text. It is important for the author to leave out details so that the reader’s imagination is activated and put to the artistically creative task of determining those story features for herself. Thus the exact same text will be imaginatively pictured and conceptually interpreted in different ways by different readers and also in different ways by the same reader upon additional readings. But the reader’s becoming artificially and imaginatively aware  of the perceptible features of the story’s elements is not the only important component of the imaginative literary experience. As well there is the awareness of what would need to be different from the reader’s given reading experience in order instead to have the experience of the story elements. So for example, to read about a mountain that is mentioned in a text involves not only creatively picturing that mountain’s details in one’s own particular way. It also involves becoming aware of what about our current situation (reading the book in a chair, for example) would need to be different in order for us to have the experience of seeing that mountain (as for example realizing the way we would be awed by it and influenced by the other perceptual and emotional components of such an experience.)

 

 

 

Summary

 

In the prior section we saw how the process of reading a literary text involves the interwoven temporal dimensions of time consciousness, even on second readings when outcomes are known in advance. Iser now notes that we cannot on the basis of the text’s contents know how the reader’s consciousness organizes and interprets the parts. [Our phenomenal consciousness constitutes the literary entities and their relations while reading. But the way those entities come to be constituted and related will vary from person to person, and even for any one person, it can vary from reading to reading.]

The impressions that arise as a result of this process will vary from individual to individual, but only within the limits imposed by the written as opposed to the unwritten text. In the same way, two people gazing at the night sky may both be looking at the same collection of stars, but one will see the image of a plough, and the other will make out a dipper. The “stars” in a literary text are fixed; the lines that join them are variable. The author of the text may, of course, exert plenty of influence on the reader’s imagination – he has the whole panoply of narrative techniques at his disposal – but no author worth his salt will ever attempt to set the whole picture before his reader’s eyes. If he does, he will very quickly lose his reader, for it is only by activating the reader’s imagination that the author can hope to involve him and so realize the intentions of his text.

(Iser 287)

 

Iser then expands upon this notion of the reader’s active, imaginative participation with the creation of the literary work. He does so by quoting Gilbert Ryle’s account of imagining a mountain. [The idea seems to be the following. Suppose there is some mountain that you are actually seeing. This engages your consciousness in a certain way, and also it presents the mountain to you in its actuality. Now suppose instead that the mountain is mentioned while you are reading a literary text. In the first case of actual seeing, there is merely a perceptual act with its normal other acts of conscious awareness. But in imagining oneself seeing the mountain, there is a more “sophisticated” act of awareness, because this imaginative act involves as well the thought of you being somewhere else and seeing the mountain. This is at least how Ryle will put it. The idea here might be something like us thinking, “I am standing in front of the mountain, and I am seeing that it has these features”. But if you were actually just standing there, you would not have this thought. You would just see the features. The second idea in Ryle’s account seems to be the following. When we imagine the mountain, we are considering not just what the mountain is like but also what would need to be different about our given experiential situation in order for it to be an actual experience of the mountain. So for example, suppose we are sitting in a comfortable chair indoors reading something that mentions the mountain. When we imagine that mountain, we become not just aware of its features. We also become aware of what it is like to be standing there seeing that mountain. In that case, we might note that unlike now where we are sitting indoors, to see the mountain would involve also hearing the sounds of wildlife, smelling the scents of a forest or pasture, feeling a cool breeze, being awed by the mountain’s majesty, and so on. Iser will emphasize the role of the mountain’s absence in the structure of the experience. But we might also think of the experiential factor here as being simply one of difference. So in Iser’s account, the structural feature of the experience that allows us to creatively imagine the mountain is the absence of that mountain from our current perceptual awareness. However, I am saying that if we are reluctant to put too much emphasis on structures of absence, we can instead say that the important structural feature here is difference. In other words, what makes it possible for us to creatively generate the artificial experience of the mountain is the fact that there is a difference between seeing it and imagining it, and we exploit that difference when creatively reading the text. Iser’s further point will be that the literary text will not give us the full experience, but it will leave out details so that we can construct those by transporting ourselves imaginatively into the situation.]

Gilbert Ryle, in his analysis of imagination, asks: “How can a person fancy that he sees something, without realizing that he is not seeing it?” He answers as follows:

Seeing Helvellyn (the name of a mountain) in one’s mind's eye does not entail, what seeing Helvellyn and seeing snapshots of Helvellyn entail, the having of visual sensations. It does involve the thought of having a view of Helvellyn and it is therefore a more sophisticated operation than that of having a view of Helvellyn. It is one utilization among others of the knowledge of how Helvellyn should look, or, in one sense of the verb, it is thinking how it should look. The expectations which are fulfilled in the recognition at sight of Helvellyn are not indeed fulfilled in picturing it, but the picturing of it is something like a rehearsal of getting them fulfilled. So far from picturing involving the having of faint sensations, or | wraiths of sensations, it involves missing just what one would be due to get, if one were seeing the mountain.¹⁰

If one sees the mountain, then of course one can no longer imagine it, and so the act of picturing the mountain presupposes its absence. Similarly, with a literary text we can only picture things which are not there; the written part of the text gives us the knowledge, but it is the unwritten part that gives us the opportunity to picture things; indeed without the elements of indeterminacy, the gaps in the text, we should not be able to use our imagination.¹¹

(Iser 287-288)

[Footnote 10: Gilbert Ryle, The Concept of Mind(Harmondsworth, 1968), p. 255.]

[Footnote 11: Cf. Iser, pp. I Iff., 42ff]

[Recalling footnote 8 from p.285: For a more detailed discussion of the function of “gaps” in literary texts see Wolfgang Iser, “Indeterminacy and the Reader's Response in Prose Fiction,” Aspects of Narrative, English Institute Essays, ed. by J. Hillis Miller (New York, 1971), pp. 1-45.]

 

Iser illustrates this fact by noting that if we first read a book then secondly see a film adaptation of it, we might be disappointed that the way the film gives visual definition and character to the story world is not how we imagined it while reading. Iser then claims that the story’s hero must be pictured and not seen. [I am not sure what is wrong exactly with seeing it. The problem might be that it ceases to be a literary text and instead becomes a show. But for our reading experience to be literary rather than cinematic or theatrical, we need to be the painter of the pictures. Iser also says that the imaginative literary experience, by being largely constructed by the reader herself, is not just a richer one but it is also “more private”. The idea here might again be the personalization of the experience. It might also have something to do with the tangible features of the story not being a public spectacle, like with film, allowing each reader to make it whatever they want it to be.] And furthermore, the problem might be that when we see it, that prevents us from revising or altering the determined qualities of the presented story elements. In a literary text, however, we have that freedom to vary the way we imagine the elements.]

The truth of this observation is borne out by the experience many people have on seeing, for instance, the film of a novel. While reading Tom Jones, they may never have had a clear conception of what the hero actually looks like, but on seeing the film, some may say, “That’s not how I imagined him.” The point here is that the reader of Tom Jones is able to visualize the hero virtually for himself, and so his imagination senses the vast number of possibilities; the moment these possibilities are narrowed down to one complete and immutable picture, the imagination is put out of action, and we feel we have some- how been cheated. This may perhaps be an oversimplification of the process, but it does illustrate plainly the vital richness of potential that arises out of the fact that the hero in the novel must be pictured and cannot be seen. With the novel the reader must use his imagination to synthesize the information given him, and so his perception is simultaneously richer and more private; with the film he is confined merely to physical perception, and so whatever he remembers of the world he had pictured is brutally cancelled out.

(Iser 288)

 

 

Main work cited:

Wolfgang Iser. “The Reading Process: A Phenomenological Approach.” New Literary History 3 (1972): 279-99.

Agler (6.2) Symbolic Logic: Syntax, Semantics, and Proof, "The Language of RL", summary

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[David Agler, entry directory]
[Agler’s Symbolic Logic, entry directory]

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.6: Predicate Language, Syntax, and Semantics

6.2 The Language of RL

 

 

 

Brief summary:

There are five elements in the language of predicate logic (RL).

1) Individual constants or names of specific items, and they are represented with lower case letters spanning from ‘a’ to ‘v’ (and expanded with subscript numerals).

2) n-place predicates, which predicate a constant or variable, or they relate constants or variables to one another. They are represented with capital letters from ‘A’ to ‘Z’ (and expanded with subscript numerals).

3) Individual variables, which can be substituted by certain constants, and they are represented with lowercase (often italicized) letters spanning from ‘w’ to ‘z’ (and expanded with subscript numerals).

4) Truth functional operators and scope indicators from the language of propositional logic (PL), namely, ¬, ∧, ∨, →, ↔, (, ), [, ], {, }.

5) Quantifiers, which indicate what portion of the set of items that can stand for a variable are to be taken into consideration in a part of a formulation. When indicating that the full portion is to be considered in some instance of a variable in a formula, we use the universal quantifier ∀. We can understand it to mean “all,” “every,” and “any.” But if we are to consider only a portion of the possible items that can substitute in for a variable, then we use the existential quantifier ∃, which can mean “some,” “at least one,” and the indefinite determiner “a.”

The purpose of the language of predicate logic is to express logical relations holding within propositions. There is the simple relation of predication to a subject, which would be a one-place predicate. There are also the relations of items within a predicate, as in “... is taller than ...”, which in this case is a two-place predicate, and so on. To say John is tall we might write Tj, and to write John is taller than Frank we could write Tjf. The number individuals that some predicate requires to make a proposition is called its adicity. And  when all the names have been removed from a predicational sentence, what remains is called an unsaturated predicate or a rheme. We might also formulate those above propositions using variables rather than constants, as in Tx and Txy. When dealing with variables, the domain of discourse D is the set of items that can be substituted for the variables in question, and this possible substitutions are called substitution instances for variables or just substitution instances. The domain is restricted if it contains only certain things and it is unrestricted if it includes all things. We may either explicitly stipulate what the domain is, which is common in formal logic, or the context of a discussion might implicitly determine the domain, and this domain can fluidly change as the discussion progresses. Also, in these cases with variables, we might further specify the quantities of the variables that we are to consider. So to say, everyone is taller than Frank we might write, (∀x)Txf. Someone is taller than Frank might be (∃x)Txf. Quantifiers have a scope in the formulation over which they apply. They operate just over the propositional contents to the immediate right of the quantifier or just over the complex propositional contents to the right of the parentheses.

 

 

Summary

 

6.2 The Language of RL

 

Agler makes the following chart displaying the elementary vocabulary of predicate logic RL.

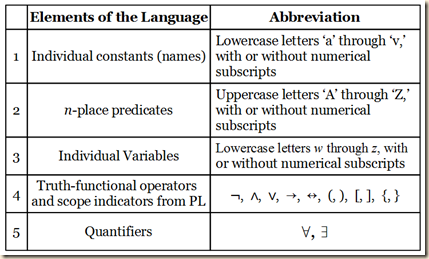
(Agler 248)

 

 

6.2.1 Individual Constants (Names) and n-Place Predicates

 

As we noted in section 6.1, we need a language that is more expressive than that language of propositional logic (PL) by “taking internal (or subsentential) features as basic” (248). We will begin by considering sentences with such logically relevant internal structures.

1) John is tall.

2) Liz is smarter than Jane.

(Agler 248)

Let us look first at 1. “John is tall.” Here we have two important internal features. On the one hand, we have the noun phrase or name John, and on the other hand we have the predicate or verb phrase is tall (Agler 248). In the second sentence, we also have proper names, Liz and Jane. In our language of predicate logic (RL), we will use lowercase letters from ‘a’ to ‘v’ for such names or constants as these. And they can optionally take subscript numerals (248). [From the examples it seems arbitrary whether or not the letter is italicized.] Agler gives these examples:

j = John

l = Liz

d₃₂ = Jane

(Agler 248)

 

Now, in RL, a name “always refers to one and only one object” and thus there are no names that fail to refer to anything. However, many names can refer to the same object. Thus for example “ ‘John Santellano’ and ‘Mr. Santellano’ can designate the same person” (249). 

 

Consider the two predicates from above, “… is tall” and “… is smarter than…”. We would consider both predicates in RL as “predicate terms”. As we can see, the predicate term in the first case only takes one individual in order to create a sentence that expresses some proposition, for example, “John is tall”. But “… is smarter than…” requires two individuals to make a proposition, as for example,  “Liz is smarter than Jane”. The number individuals that some predicate requires to make such a proposition is called its adicity. Thus the adicity of “… is tall” is one, and the adicity of “… is smarter than…” is two (249).

 

As we noted before, we use capital letters to express predicates and relations, using any letters from A to Z. And we again may use numerical subscripts so that we can have more than 26 distinct predicates if we need. Agler gives these examples:

T = is tall

G = is green

R = is bigger than

F₄₃ = is faster than

(249)

 

We also use the same truth-functional operators as in PL. We now will examine how to translate English sentences with names and predicates into RL. Agler has us recall sentence 1: John is tall. The first step is to replace its names with blanks and to assign names with letters. So we would have:

John is tall.

____ is tall

j = John

(Agler 249)

There is only one name in this sentence, so the predicate’s adicity is 1. Now, “After all names have been removed what remains is called an unsaturated predicate or a rheme” (249). We can now assign to the unsaturated English predicate a capital letter. So in all we now have:

John is tall.

____ is tall

j = John

T = ___ is tall

(Agler 249)

Now we will finally formulate the structure. [Consider that in English the predicate normally comes after the subject. In these formulations, we put the predicate symbol before the terms that the predicate is relating or predicating.] Using our above equivalences, we would make this translation:

John is tall.

Tj

(Agler 250)

 

Let us now consider a sentence with a two-place predicate, and we will give also the equivalences and final formulation.

John is taller than Frank.

j = John

f = Frank

R = ___ is taller than ___

Rjf

(Agler 250)

[There is not yet an explicit discussion of the order, but it seems that the order of the individual variables follows the order in the English sentence. I am not sure about situations where the order is not logically important even in the English formulation, as in the case of “John stands between Liz and Jane” and “John stands between Jane and Liz”.]

 

In our natural use of English it might be awkward to use predicates that take very many individuals, we still leave it as a possibility in RL to have large adicities. “Since there is no need to put a restriction on how many objects we can relate together, what remains after all object terms have been removed is an n-place predicate, where n is the number of blanks or places where an individual constant could be inserted” (250).

 

Agler then gives an example of a three-place predicate.

John is standing between Frank and Marry.

j = John

f = Frank

m = Mary

S = __ is standing between __ and __

Sjfm

(Agler 250)

 

 

 

6.2.2 Domain of Discourse, Individual Variables, and Quantifiers

 

Agler has us consider three sentences that cannot be adequately expressed merely in PL.

(3) All men are mortal.

(4) Some zombies are hungry.

(5) Every man is happy.

(Agler)

 

Previously, as with “John is tall”, we were only predicating a property to one individual. But now in these sentences we “predicate a property to a quantity of objects” (251). So we cannot simply use the formulation structures from above. Instead, as for sentence 4, we need to express “the more indefinite proposition that some object in the universe is both a zombie and is hungry” (251).

 

For such sentences as 3-5, we will need to introduce “two new symbols and the notion of a domain of discourse” (251). [The domain of discourse is all the things we might refer to in some usage of RL. In this we can have variables which may take the value of some thing in the domain of discourse. They are called individual variables and they will be symbolized with lowercase letters from w to z, and it seems they should be italicized. (Recall that individual constants, the names like John and so on, took letters ‘a’ through ‘v’ and were not in most cases italicized.) Such individual variables are like the blanks from before.]

For convenience, let’s abbreviate the domain of discourse as D and use lowercase letters w through z, with or without subscripts, to represent individual variables. The domain of discourse D is all of the objects we want to talk about or to which we can refer. So, if our discussion is on the topic of positive integers, then we would say that the domain of discourse is just the positive integers. Or, more compactly,

D: positive integers

If our discussion is about human beings, then we would say that the domain of discourse is just those human beings who exist or have existed. That is,

D: living or dead humans

 

Individual variables are placeholders whose possible values are the individuals in the domain of discourse. Individual variables are said to range over individual particular objects in the domain in that they take these objects as their values. Thus, if our discussion is on the topic of numbers, an individual variable z is a placeholder for some number in the universe of discourse.

As placeholders, we can also use variables to indicate the adicity of a predicate. Previously we indicated this by using blanks (e.g., ____ is tall). Rather than representing a predicate as a sentence with a blank attached to it, we will fill in the blanks with the appropriate number of individual variables:

Tx = x is tall

Gx = x is green

Rxy = x is bigger than y

Bxyz = x is between y and z.

(Agler 251)

 

Agler then distinguishes two ways that we determine the domain of discourse. 1) Stipulatively: here we name the objects that are in the domain. So if “the objects to which variables and names can refer are limited to human beings”, then we would write:

D: human beings

(252)

[I am not sure, but I would also think that another stipulative way is to list the individual members of the set.] So suppose a person says, “Everyone is crazy”. Since they presumably are speaking about humans, the domain of discourse D is human beings, and thus their statement is shorthand for “Every human being is crazy” (252).

 

In normal conversation, however, we do not often explicitly stipulate our domain of discourse, and in fact it might change throughout the conversation and at times or always be very difficult to determine precisely. Instead, the domain is often determined 2) contextually, so depending on what we are saying, it might be that our domain of discourse is colors or in another case human beings living in the 1900s. And the domain can often change with the flux of contextual factors. “If you and your friends are talking about movies, then the D is movies, but the D can quickly switch to books, to mutual friends of yours who behave similarly to characters in books, and so on” (252). In our uses here of RL, we will always stipulate our domain (252).

 

Agler then notes another distinction with regard to domains. They are either restricted or unrestricted. It is restricted if the domain is limited to some set of things and does not extend to others. Suppose we are doing arithmetic. Our domain is restricted to the domain of numbers. Or if we are talking about paying taxes, our domain is restricted to humans (252). But consider instead we say “Everything is crazy”. The “everything” here supposedly means not just some types of things but in fact all things no matter what. “If I wrote, Everything is crazy, this proposition means, for all x, where x can be anything at all, x is crazy. This includes humans, animals, rocks, and numbers” (252). [The next idea complicates this point a little bit. It seems that we cannot necessarily infer that the domain is restricted merely from the meanings of the terms used. We might think that in the statement “Everyone is crazy” that we are thereby automatically dealing with a restricted domain that is limited to humans. But it seems that we can also use this statement even when stipulating that we are using an unrestricted domain. Yet if we do so, we must specify that we are dealing with a limited subset of that that unrestricted domain. Let me quote as I may have it wrong:]

Another example: suppose you were to say, Everyone is crazy, in an unrestricted domain. Here, it is implied that you are only referring to human beings. But since you are working in an unrestricted domain, it is necessary to specify this. Thus, Everyone is crazy is translated as for any x in the domain of discourse, if x is a human being, then x is crazy.

(252)

 

[As we noted before, the domain limits what the variables can refer to. This means it limits what objects can be substituted for those variables. The term for those limited sets of objects is substitution instances for variables or substitution instances.]

The domain places a constraint on the possible individuals we can substitute for individual variables. We will call these substitution instances for variables, or substitution instances for short. For example, discussing the mathematical equation ‘x + 5 = 7,’ the domain consists of integers and not shoes, ships, or people. If someone were to say that a possible substitution instance for x is ‘that patch of green over there,’ we would find this extremely strange because the only objects being considered as substitution instances are integers and not patches of green. Likewise, if someone were to say, ‘Everyone has to pay taxes,’ and someone else responded, ‘My cat does not pay taxes,’ we would take this to be strange because the only objects being considered as substitution instances are people and not animals or numbers or patches of green. Thus, it is important to note that the domain places a limitation on what can be a instance of a variable.

(Agler 252)

 

Agler will now examine the quantifiers. There are two in RL.

1)  Universal quantifier: ∀. In English, “all,” “every,” and “any.”

2)  Existential quantifier: ∃. In English, “some,” “at least one,” and the indefinite determiner “a.”

(Agler 252-253, not exact quotation)

 

Let us consider the first case with the example sentence:

6)  Everyone is mortal.

[Here our predicate is: ... is mortal. And the “everyone” should be reinterpreted in terms of a quantifier and a variable.] We could reexpress 6 in a number of ways:

6a)   For every x, x is mortal.

6b)   All x’s are mortal.

6c)   For any x, x is mortal.

6d)   Every x is mortal.

Let us stick with the first formulation, but we will use parentheses [for some reason, perhaps to clarify the different parts of the formulation, namely, the quantification part and the predication part.]

6*)  (For every x)(x is mortal)

(Agler 253)

Now let us say that

Mx = x is mortal

[We now have something like:

(For every x)Mx

]

We will replace the for every x with the symbol for universal quantification to get:

6_RL)   (∀x)Mx

 

Now let us look instead at existential quantification with the following example sentence:

7)  Someone is happy.

[Here our predicate is: “... is happy”.] We could express it also as:

7a)  For some x, x is happy.

7b)  Some x’s are happy.

7c)  For at least one x, x is happy.

7d)  There is an x that is happy.

(Agler 253)

These would be equivalent to:

7*)   (For at least one x)(x is happy)

Hx will stand for x is happy. [So we now have something like:

(For at least one x)Hx

] We will replace for at least one x with the existential quantifier to get:

7_RL)   (∃x)Hx

(Agler 253)

 

 

 

6.2.3 Parentheses and Scope of Quantifiers

 

Recall from PL how we used parentheses to remove potential ambiguities regarding how to group the propositional letters that are related or modified by operators in complex expressions. For example, without parentheses, in the formula A∨B∧C we do not know if its nesting structure is (A∨B)∧C or A∨(B∧C). This is essential, as the two different groupings have different logical properties. Thus A∨B∧C is not a well-formed formula in PL. In RL, parentheses also have this same disambiguating function. But they have another function as well. They are also used to indicate the range or scope of the quantifier (254). [Note, Suppes discusses these topics in section 3.5 of his Introduction to Logic.]

 

Agler states how we are to understand the scope of the quantifier in the following way:

The ‘∀’ and ‘∃’ quantifiers operate over the propositional contents to the immediate right of the quantifier or over the complex propositional contents to the right of the parentheses.

(Agler 254)

He has us consider these examples:

1)   (∃x)Fx

2)   ¬(∃x)(Fx∧Mx)

3)   ¬(∀x)Fx∧(∃y)Ry

4)   (∃x)(∀y)(Rx↔My)

(Agler 254)

 

Let us begin with the first one:

1)   (∃x)Fx

There is only one thing to the right of the quantifier, so it ranges over Fx. What about the second one?

2)   ¬(∃x)(Fx∧Mx)

Here there is a formulation within parentheses, and there is only one such enclosed formula. So since the quantifier in these cases ranges “over the complex propositional contents to the right of the parentheses”, it would for sentence 2 range over (Fx∧Mx). Now let us consider sentence 3.

3)   ¬(∀x)Fx∧(∃y)Ry

(Agler 254)

Here we have two quantifiers. The ∀x does not range over both constituent propositions, because they are not both enclosed in parentheses. It only ranges over the formula to its right and thus only to Fx. For the same reason, the ∃y only ranges over Ry. Now what about the fourth sentence?

4)   (∃x)(∀y)(Rx↔My)

[We might want to say here that the ∃x applies to just (Rx↔My), but for reasons that we may perhaps learn later, it somehow also applies to the other quantifier too.] Here, the ∃x operates on (∀y)(Rx↔My), [because that is what is to its right.] But ∀y only operates on Rx↔My.

 

Agler now shows why scope becomes important when translating English sentences in RL and vice versa. We consider the following equivalences:

Ix = x is intelligent

Ax = x is an alien

(Agler 254)

Let us now see two similar ways to apply quantification to a conjunction of these formulations.

5)   (∃x)(Ix)∧(∃x)(Ax)

6)   (∃x)(Ix∧Ax)

(Agler 254)

At first glance, we might want to say that their meanings are identical. However, “they express different propositions and are true and false under different conditions” (254). The main idea is that in sentence 5, there could be two things, with one being intelligent and the other being an alien. This is because the quantifier only ranges over the formula to its right and does not apply to both. However, proposition 6 means that there is just one thing (or some group of things treated dually in each sub-proposition) that is both intelligent and an alien. Also these formulations are not true and are not false under the same conditions, and hence they are not logically equivalent. Thus, “Proposition (5) will be true, for example, if a stupid alien exists and some intelligent dolphin exists” (254). However, that situation does not make sentence 6 true, because it would need that the predicates apply to the same creature(s). So if the situation is that there is a stupid alien but an intelligent dolphin, 5 is true but 6 is false. [Yet, perhaps any situation that makes 6 true also makes 5 true, but I am not sure.]

 

Agler notes a helpful parallel between the scope of negation and the scope of quantification.

In each of the above cases, parentheses are used to determine what is within the scope of a quantifier. There is thus a parallel between how the scope of quantifiers is determined and how the scope of negation is determined. For example, the negation in ‘¬(P∧Q)’ applies to the conjunction ‘P∧Q,’ while the negation in ‘¬P∧Q’ applies only to the atomic ‘P.’ This is the same for quantifiers since (∀x) in ‘(∀x)(Px→Qx)’ applies to the conditional ‘Px→Qx,’ while (∀x) in ‘(∀x)(Px)∧(∀y)(Qy)’ applies only to ‘Px.’

(Agler 255)

 

Agler offers more examples to clarify further how scope works with quantifiers.

7)   (∃x)(Px∧Gy)∧(∀y)(Py→Gy)

Here, Px∧Gy falls under the scope of just ∃x, while Py→Gy only falls under ∀y. Now consider:

8)   (∃x)[(Mx→Gx)→(∃y)(Py)]

Under the scope of ∃x is the entire formulation [(Mx→Gx)→(∃y)(Py)]. But only Py falls under the scope of ∃y. And what about the following one?

9)   (∀z)¬(Pz∧Qz)∧(∃x)¬(Px)

Here, just ¬(Pz∧Qz) falls under the scope of ∀z and just ¬(Px) falls under the scope of ∃x.   (Agler 255)

 

 

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.

 

Agler (6.1) Symbolic Logic: Syntax, Semantics, and Proof, "The Expressive Power of Predicate Logic", summary

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[David Agler, entry directory]
[Agler’s Symbolic Logic, entry directory]

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.6: Predicate Language, Syntax, and Semantics

6.1 The Expressive Power of Predicate Logic

 

 

 

Brief summary:

While everything in the language of propositional logic (PL) can be expressed in English, not everything in English can be expressed in PL. In PL, propositions are treated as whole units (symbolized as singular letters) without regard to logical properties internal to the sentences, as for example between subject and predicate and with respect to quantification. Thus we will examine a more expressive language of predicate logic (RL), which is a logic of relations.

 

 

 

Summary

 

We previously examined the language, syntax, and semantics of propositional logic (PL). Agler notes now two of PL’s strengths, namely, that we may apply it to English and there are decision procedures for testing for such logical properties as validity, consistency and so on.

The language, syntax, and semantics of PL have two strengths. First, logical properties applicable to arguments and sets of propositions have a corresponding applicability in English. So, if one is dealing with a valid argument in PL, then that argument is also valid for English. Second, the semantic properties of arguments and sets of propositions have decision procedures. That is, there are mechanical procedures for testing whether any argument is valid, whether propositions in a set have some logical property (e.g., they are consistent, equivalent, etc.), and whether any proposition is always true (a tautology), always false (a contradiction), or neither always true nor always false (a contingency).

(Agler 247)

 

But what is PL’s weakness? [It seems that the idea we noted above is that whatever is expressed in PL can be expressed in English. However, the idea now seems to be, not everything that we can express in English can be expressed in PL. We see this with quantification. When we use quantifiers in English, like “all” and “some”, the way such sentences relate can have certain logical properties that are not evident in PL. For, in PL we would not modify any proposition with a quantifier. All sentences, regardless of whether they have quantifiers – and if they do, regardless of which quantifier they have – are treated generically as units, symbolized by singular propositional letters. So inferences based on sentences using quantifiers can appear valid in PL, but were we to examine the sentences themselves, our intuition could tell us the inferences are invalid. What is needed, then, is a language that expresses the logical properties that a) hold between the parts within a proposition and b) are relevant to the logical properties a proposition might itself have or have in relation to others.] PL’s weakness is that it does not express certain kinds of internal logical properties of certain sentences. Instead we will discuss a more expressive language that takes into account the subjects and predicates of sentences, which is called the language of predicate logic, abbreviated RL, because it is a logic of relations.

The weakness of PL is that it is not expressive enough. That is, some valid arguments and semantic relationships in English cannot be expressed in propositional logic. Consider the following example:

All humans are mortal.

Socrates is a human.

Therefore Socrates is a mortal.

This argument is clearly valid in English but cannot be expressed as a valid argument in PL. Symbolically, the argument is represented as follows:

M

S

R

The above argument is clearly invalid. In order to bring English arguments like the one above into the domain of symbolic logic, it is necessary to develop a formal language that does not symbolize sentences as wholes (e.g., John is tall as ‘J’), but symbolizes parts of sentences. That is, a formal language whose basic unit is not a | complete sentence but the subject(s) and predicate(s) of the sentence such a language will be more expressive and able to represent the above argument as valid. This is the language of predicate logic (sometimes called the logic of relations). We’ll symbolize it as RL.

(Agler 247-248)

 

 

 

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.

 

Agler (5.6) Symbolic Logic: Syntax, Semantics, and Proof, "Additional Derivation Strategies", summary

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[David Agler, entry directory]
[Agler’s Symbolic Logic, entry directory]

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.5: Propositional Logic Derivations

5.6 Additional Derivation Strategies

 

 

 

Brief summary:

After revising our strategic rules for proof solving, they are in their entirety the following [the first three being this section’s modifications]:

SP#1(E+): First, eliminate any conjunctions with ‘∧E,’ disjunctions with DS or ‘∨E,’ conditionals with ‘→E’ or MT, and biconditionals with ‘↔E.’ Then, if necessary, use any introduction rules to reach the desired conclusion.

SP#2(B): First, work backward from the conclusion using introduction rules (e.g., ‘∧I,’‘∨I,’‘→I,’‘↔I’). Then, use SP#1(E).

SP#3(EQ+): Use DeM on any negated disjunctions or negated conjunctions, and then use SP#1(E). Use IMP on negated conditionals, then use DeM, and then use SP#1(E).

SA#1(P,¬Q): If the conclusion is an atomic proposition (or a negated proposition), assume the negation of the proposition (or the non-negated form of the negated proposition), derive a contradiction, and then use ‘¬I’ or ‘¬E.’

SA#2(→): If the conclusion is a conditional, assume the antecedent, derive the consequent, and use ‘→I.’

SA#3(∧): If the conclusion is a conjunction, you will need two steps. First, assume the negation of one of the conjuncts, derive a contradiction, and then use ‘¬I’ or ‘¬E.’ Second, in a separate subproof, assume the negation of the other conjunct, derive a contradiction, and then use ‘¬I’ or ‘¬E.’ From this point, a use of ‘∧I’ will solve the proof.

SA#4(∨): If the conclusion is a disjunction, assume the negation of the whole disjunction, derive a contradiction, and then use ‘¬I’ or ‘¬E.’

(Agler 199; 216)

 

 

 

Summary

 

5.6 Additional Derivation Strategies

 

Since we previously added six new derivation rules, we will need to revise our proof strategies to accommodate them (Agler 116). Agler lists them first, then we proceed through them individually:

SP#1(E+): First, eliminate any conjunctions with ‘∧E,’ disjunctions with DS or ‘∨E,’ conditionals with ‘→E’ or MT, and biconditionals with ‘↔E.’ Then, if necessary, use any introduction rules to reach the desired conclusion.

SP#2(B): First, work backward from the conclusion using introduction rules (e.g., ‘∧I,’ ‘∨I,’ ‘→I,’ ‘↔I’). Then, use SP#1(E).

SP#3(EQ+): Use DeM on any negated disjunctions or negated conjunctions, and then use SP#1(E). Use IMP on negated conditionals, then use DeM, and then use SP#1(E).

(Agler 216)

 

To illustrate the first rule, he has us consider

P→Q, ¬Q, P∨R, R→W ⊢ W

[Recall the rule: “SP#1(E+) First, eliminate any conjunctions with ‘∧E,’ disjunctions with DS or ‘∨E,’ conditionals with ‘→E’ or MT, and biconditionals with ‘↔E.’ Then, if necessary, use any introduction rules to reach the desired conclusion” (216).] Let us set it up.

SP#1(E+) tells us to make as many eliminations as possible. As we can see, we can use MT using lines 1 and 2.

And then now we can use DS using lines 3 and 5.

And finally we can use conditional elimination to obtain our goal proposition.

 

Agler shows another proof that demonstrates this first revised rule.

(P∧M)∧(¬Q∨R), P→L, P↔T, ¬R∧W ⊢ (L∧T)∧¬Q

(Agler 217)

First we set it up.

We have some conjunctions that will allow us to derive simpler propositions through elimination. And perhaps this will give us parts to make other sorts of eliminations. Since out goal proposition is made of conjunctions, we can try to build it back up using conjunction introduction. We might start by using elimination on the first line.

And we can use it again on the fourth line.

We see also that we can use conjunction elimination on our derived line 5.

That is all the conjunctions. But we see now that we can make other eliminations. We can use conditional elimination on line 2.

And we can use biconditional elimination on line 3.

And finally, we can use disjunctive syllogism on line 6.

This gives us all the parts we need to build up our goal proposition. So we do the nested conjunction first.

And we complete it in this way.

(Agler 218)

 

Recall the third strategic rule

SP#3(EQ+): Use DeM on any negated disjunctions or negated conjunctions, and then use SP#1(E). Use IMP on negated conditionals, then use DeM, and then use SP#1(E).

(Agler 218)

 

To illustrate, he has us consider this argument:

¬[P∨(R∨M)], ¬M→T ⊢ T

(Agler 218)

Let us set it up.

We can see in the first line that we can apply De Morgan’s Law.

This gives us a conjunction that can be decomposed.

We can now use De Morgan’s Law on line 5.

Now with line 7, we can derive our goal proposition.

(Agler 219)

 

 

5.6.1 Sample Problem

 

Agler will now give a complicated example using a few nested assumptions to show an instance where we would make multiple uses of the rules.

⊢ [P→(Q→R)]→[(¬Q→¬P)→(P→R)]

(Agler 219)

 

Now, let us look at all our strategic rules together.

SP#1(E+): First, eliminate any conjunctions with ‘∧E,’ disjunctions with DS or ‘∨E,’ conditionals with ‘→E’ or MT, and biconditionals with ‘↔E.’ Then, if necessary, use any introduction rules to reach the desired conclusion.

SP#2(B): First, work backward from the conclusion using introduction rules (e.g., ‘∧I,’‘∨I,’‘→I,’‘↔I’). Then, use SP#1(E).

SP#3(EQ+): Use DeM on any negated disjunctions or negated conjunctions, and then use SP#1(E). Use IMP on negated conditionals, then use DeM, and then use SP#1(E).

SA#1(P,¬Q): If the conclusion is an atomic proposition (or a negated proposition), assume the negation of the proposition (or the non-negated form of the negated proposition), derive a contradiction, and then use ‘¬I’ or ‘¬E.’

SA#2(→): If the conclusion is a conditional, assume the antecedent, derive the consequent, and use ‘→I.’

SA#3(∧): If the conclusion is a conjunction, you will need two steps. First, assume the negation of one of the conjuncts, derive a contradiction, and then use ‘¬I’ or ‘¬E.’ Second, in a separate subproof, assume the negation of the other conjunct, derive a contradiction, and then use ‘¬I’ or ‘¬E.’ From this point, a use of ‘∧I’ will solve the proof.

SA#4(∨): If the conclusion is a disjunction, assume the negation of the whole disjunction, derive a contradiction, and then use ‘¬I’ or ‘¬E.’

(Agler 199; 216)

We do not have any propositions, so we need to begin with an assumption. The question is, which assumption rule should we use? As we can see, we use SA#2(→), “If the conclusion is a conditional, assume the antecedent, derive the consequent, and use ‘→I.’”

So let us set it up by assuming the antecedent.

Now, at this point we cannot make any further eliminations. [One operation we might perform is IMP to get ¬P∨(Q→R). Agler does not take this route, perhaps because it is either inefficient or ineffectual.] One option we have at this point is to make a second assumption. Recall that the point of this assumption is to derive the consequent of the goal proposition. That consequent is:

(¬Q→¬P)→(P→R)

To obtain this, we could assume the antecedent.

Now again, no elimination rules apply to this formula. We recall that we want to finally derive the consequent of this subgoal proposition, so we want to derive P→R. One option would be to assume P with hopes to derive R.

The question is now, how can we derive R? We see that we can use implication elimination on line 1 and 3 to obtain Q→R. After that we would just need a way to derive Q. So let us do that.

Since we have P, that means we could use Modus Tolens to get Q, but we have to work through some double negations. Let us derive a doubly negated P from line 3.

Then with Modus Tolens we can get a doubly negated Q from line 2.

From this we can derive Q.

Which we needed to derive R in line 4.

And we needed R to derive P→R in the next outer subproof, which we do using conditional introduction.

We needed that to obtain the consequent of the goal proposition.

And again using conditional introduction, we can produce the whole goal proposition.

(Agler 221)

 

Agler notes another effective way to complete the proof. Let us go back to step 3.

[Recall this strategic assumption rule: “SA#1(P,¬Q) If the conclusion is an atomic proposition (or a negated proposition), assume the negation of the proposition (or the non-negated form of the negated proposition), derive a contradiction, and then use ‘¬I’ or ‘¬E.’”] Instead of using SA#2(→) like above, we can notice that the goal proposition is R, and thus is atomic. That means we can also use SA#1(P,¬Q), where we assume the negation of R and derive a contradiction. So let us do that.

Now how will we derive a contradiction? [One way might be to use IMP on line 1 to get Q implies R. Then using Modus Tolens on that and line 4 we get negated Q. Then with conditional elimination on line 2 we get negated P, which contradicts the assumption in line 3.] We might see one possibility already, since we have P in line 3 and negated P as the consequent in line 2. If we can just find negated Q, then we can obtain that contradiction of P and negated P. We will do this by working through the conditional in line 1. So we use conditional elimination on line 1 to get Q implies R.

Then using Modus Tolens we can obtain negated Q.

Then with conditional elimination on 2 we can derive negated P.

This contradicts P in line 3, so let us reiterate it to expose that contradiction in the lowest subproof.

That contradiction allows us to derive the non-negated form of our assumption, so we obtain R in the next outer subproof.

From this point on we follow the same procedure as before.

(Agler 222)

 

 

 

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.

 

Agler (5.5) Symbolic Logic: Syntax, Semantics, and Proof, "Additional Derivation Rules (PD+)", summary

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[David Agler, entry directory]
[Agler’s Symbolic Logic, entry directory]

[The following is summary. Boldface (except for metavariables) and bracketed commentary are my own. Please forgive my typos, as proofreading is incomplete. I highly recommend Agler’s excellent book. It is one of the best introductions to logic I have come across.]

 

 

 

Summary of

 

David W. Agler

 

Symbolic Logic: Syntax, Semantics, and Proof

 

Ch.5: Propositional Logic Derivations

5.5 Additional Derivation Rules (PD+)

 

 

 

Brief summary:

The set of 11 “intelim” propositional derivation rules, called PD, just by themselves can lead to lengthy proofs, so to them we add six more rules, to make a system called PD+. The following chart shows all of PD+, with the new ones being 13-17.

 

 

 

 

 

Summary

 

5.5 Additional Derivation Rules (PD+)

 

We previously discussed 11 “intelim” derivation rules in a system of propositional derivation called PD. With only these rules, making proofs can at times be cumbersome. So Agler adds six more rules, which in addition to the prior 11, make PD+.

 

 

5.5.1 Disjunctive Syllogism (DS)

 

We begin with the derivation rule called disjunctive syllogism (DS). [Let us first think semantically about disjunctions. We made this truth table evaluation.

The disjunction is false only when both disjuncts are false. But suppose that we begin by knowing that the disjunction as a whole is true. In our table, that limits us to the first three rows. And suppose further that we learn that one of the disjuncts is false, although we do not necessarily know the truth value of the other disjunct. So this limits us to the second and third row of the table. As we see, in both cases, whenever one disjunct is false, the other is true.] The way DS works is that if we have a disjunction and if we have also the negation of one of the disjuncts given on its own, then we can derive the other disjunct.

 

Agler will now demonstrate the usefulness of adding DS to our other rules, and he will do so by showing that in certain cases, if we do not use it, the proof can get quite complicated. His example is:

P∨Q, ¬Q ⊢ P

(209)

As we can see, this involves a fairly complex proof, when we only use our PD rules.

[Now note that were we to use the DS rule, we have everything we need already in our two premises.] But with the DS rule at our disposal, here is the proof for the exact same argument.

 

Or consider this argument:

P↔(Q∨R), P, ¬Q ⊢ R

(Agler 210)

Using just PD we would proof it like this.

But with the option of DS, we can solve it much more efficiently.

(210)

 

We should be sure not to make the following mistake. We begin with a disjunction. We also have one of the disjuncts. Then we derive the other disjunction. This is wrong. The only way DS works is if we have the negation of one of the disjuncts (210).

 

 

5.5.2 Modus Tollens (MT)

 

Now we turn to the modus tollens (MT) derivation rule. Suppose we begin with a conditional, and we also have the negation of the consequent. We can then derive the negation of the antecedent. [Again see this first semantically from the truth tables.

First suppose that we know the whole conditional is true. That limits us to lines 1, 3, and 4. And suppose further that we also know that the consequent is false. This leaves us only with line 4, where the antecedent is false.]

 

Agler shows how MT can simply proofs. Consider first:

P→Q, ¬Q  ⊢ ¬P

(Agler 211)

However, we could skip steps 3-5 using MT.

 

We can see MT work even with more complex propositions as the parts of the conditionals, as in this case:

(P∧Z)→(Q∨Z), ¬(Q∨Z) ⊢ ¬(P∧Z)

(Agler 211)

(Agler 211)

 

 

5.5.3 Hypothetical Syllogism (HS)

 

Suppose we have two conditionals, and the consequent of one is the antecedent of the second. Using Hypothetical syllogism (HS) we can then derive a conditional with the antecedent of the first with the consequent of the second.

(Agler 211)

 

We can use HS to simplify proofs for arguments with multiple conditionals [sharing middle terms]. Consider the following one:

P→Q, Q→R ⊢ P→R

(Agler 212)

As we can see, this can be solved with just one additional step beyond the premises, if we use HS. Agler shows the longer way, to illustrate its usefulness.

(Agler 212)

 

 

5.5.4 Double Negation (DN)

 

The double negation derivation rule (DN) allows us to go from a doubly negated proposition to an unnegated form, and vice versa.

This makes it an equivalence rule, and so it can be written:

P ⊣ ⊢ ¬¬P

which combines the following two derivation rules:

P ⊢ ¬¬P
¬¬P ⊢ P

(Agler 212)

 

One important thing to note about DN is that it can apply not only to complex propositions on a whole but also to any constituent proposition in a complex one.

(Agler 212-213)

 

The elimination of a double negation only works when there are two negations side-by-side, without a parenthesis or other operators or terms between them. And when we introduce double negations, they likewise must be placed side-by-side: “the rule demands that a single proposition can be replaced with a proposition that is doubly negated or a single doubly negated proposition can be replaced by removing its double negation” (213).

 

 

5.5.5 De Morgan’s Laws (DeM)

 

 

De Morgan’s Laws (DeM) will allow us to deal “with negated conjunctions and negated disjunctions” “by introducing an equivalence rule that allows for expressing every negated conjunction in terms of a disjunction and every negated disjunction in terms of a conjunction” (213).

De Morgan's Laws will enable us to shorten many proofs. Agler has us consider the proof for

¬(P∧Q) ⊢ ¬P∨¬Q

(Agler 213)

With the help of DeM, we can simplify this to one step.

(Agler 214)

 

DeM is also useful for making derivations that allow for elimination rules. Consider:

¬(P∨Q) ⊢ ¬P

We cannot apply any elimination rules directly to ¬(P∨Q). But if we make a DeM derivation, we can.

(Agler 214)

 

 

5.5.6 Implication (IMP)

 

Although our derivation rules will not allow us to derive something directly from a negated biconditional, we do have a rule, Implication (IMP) that will allow a derivation from a negated conditional. It is an equivalence rule that allows us to derive a negated conjunction from a conditional and vice versa.

 

Agler illustrates by having us consider the following.

P→Q ⊢ ¬P∨Q

(Agler 215)

Agler will show how without IMP, the proof for this can be quite long. [Recall the strategic rule SA#4(∨): If the conclusion is a disjunction, assume the negation of the whole disjunction, derive a contradiction, and then use ‘¬I’ or ‘¬E.’ (Agler 199)] Since in this proof we have a disjunction, we should follows strategic assumption rule 4 and assume the negation of the entire disjunction, with the aim of deriving a contradiction. We see below how lengthy that process can be.

[Note, in my version of the text, the justification for line 4 reads “1∧E”.] But all these derivations can be achieved in just one step using IMP.

(Agler 215)

 

Agler then compares two ways to make the proof for:

¬P∨Q ⊢ P→Q

(Agler 215)

[Recall strategic assumption rule SA#2(→): If the conclusion is a conditional, assume the antecedent, derive the consequent, and use ‘→I.’] As we can see, the conclusion is a conditional, P→Q, so in accordance with SA#2, we should assume P and try to derive Q. As we can see, we can do so using disjunctive syllogism.

(Agler 215)

But we can solve it in one step using IMP [like above] (215).

 

Agler says that IMP also helps with proofs involving negated conditionals. He has us consider:

¬(P→Q) ⊢ ¬Q

(Agler 216)

 

Let us set it up first.

We first use our new rule IMP.

We see we have a negated disjunction. At this point, we do not have  any way to apply an elimination rule, which we will need to derive our atomic goal proposition ¬Q. But since it is a negated conjunction,we could use De Morgan’s laws.

We now have a conjunction containing our goal proposition. So we can use conjunction elimination.

(Agler 216)

 

 

 

 

 

Agler, David. Symbolic Logic: Syntax, Semantics, and Proof. New York: Rowman & Littlefield, 2013.