Wikibooks: Set Theory, “Ordered Pairs”, summary

by Corry Shores

[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]
[Logic & Semantics, Entry Directory]
[Set Theory, entry directory]
[Wikibooks: Set Theory, entry directory]

 

[My commentary is in brackets.]

 

 

Summary of

 

Wikibooks: Set Theory

 

Relations

 

Ordered Pairs

 

 

Brief summary: 
In a set, the order of the members does not matter. But since we will want to work with relations, we will need groupings where the order does matter. We notate an ordered pair as (a, b) [rather than with curly braces, as with sets], and here the order of the terms does matter.

 

Summary

 

 

[Previously we were dealing with sets where the order of the members did not matter. Recall that the set was defined in the following way: “A mathematical set is defined as an unordered collection of distinct elements.” But now we will discuss relations of  sets. This will mean that one set will be related to another or to others. With that in mind, when notating this relation, the order will matter, since not all relations are symetrical. I am not sure, but in the ordered pairs we work with, we will drop the set braces, so they perhaps are not sets strictly speaking. So to understand the first formulation they will give, consider sets a, b, c, and d. And suppose that a=d and b=c. We put them into these pairings: (a, b) and (c, d). Now, if ordered mattered in the pairings, then these two pairings would not be equal, because the a is in the first position but the d is in the second. Now suppose instead that a=c and b=d. And we keep the same pairings: (a, b) and (c, d). Now we can say they are equal: (a, b) = (c, d).]

To define relations on sets we must have a concept of an ordered pair, as opposed to the unordered pairs the axiom of pair gives. To have a rigorous definition of ordered pair, we aim to satisfy one important property, namely, for sets a,b,c and d, .
(Wikibooks)

[The next part I do not understand very well; but let me quote it first, and then I will discuss it.]

As it stands, there are many ways to define an ordered pair to satisfy this property. A simple definition, then is . (This is true simply by definition. It is a convention that we can usefully build upon, and has no deeper significance.)

Theorem

Proof

If and , then .
Now, if then . Then , so and a=c.
So we have . Thus meaning .

If , we have and thus so .

If , note , so
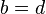
(Wikibooks)

[I did not understand the arbitrary definition of (a, b) = {{a},{a,b}}. After searching a bit, I found an excellent explanation by Arturo Magidin. The main idea is that it is not a definition in the sense that we normally think of them. The formulation {{a},{a,b}} does not intuitively present conceptual content that helps us understand why the order of the terms holds in (a, b). Rather, this definition of (a, b) as {{a},{a,b}} happens to allow us to form a proof for

(a, b) = (c, d) ↔ a=c ∧ b=d

. So all that is important is how this definition works in the proof, and not how it helps us understand the property itself. Here is the explanation by Arturo Magidin:

This definition is part of a way to try to define a lot of the things that we use in mathematics on the basis of an axiomatic theory; in this case, we start with Axiomatic Set Theory, where the only notions we have (if we are working in Zermelo-Fraenkel Set Theory) are “set” and “is and element of”, together with the axioms that tells us properties of sets and things we can do with sets.

We want to have something that works like what we know as "the ordered pair"; but all we have to work with are sets. So we need to find a way of constructing a set that has the properties we want for the ordered pair.

For a metaphor: the ordered pair is like a car; we know how to drive. But in order to actually have a car, there needs to be an engine and gasoline, and the engine has to work. We are trying to construct that engine so that we can later drive it.

So this is not notation, this is a definition of what the ordered pair is in set theory. We are defining an object, which we call “(a,b)”, to be the given set. It's not merely how we are writing the ordered pair, is what the ordered pair is if you are interested in actually seeing the engine of the car working. We know what we want “ordered pair” to behave like, but we have to actually construct an object that behaves that way. This is a way of defining an object that does behave that way.

There aren’t “two notations” here. We define “the ordered pair with first component a and second component b” to be the set

{{a},{a,b}},

(which one can prove is indeed a set using the Axioms of Set Theory, if a and b are already in the theory).

Then we prove that “the ordered pair with first component a and second component b” is equal to “the ordered pair with first component c and second component d” if and only if a=c and b=d.

Then we abbreviate “the ordered pair with first component a and second component b” by writing “(a,b)” (or sometimes “⟨a,b⟩”).

“(a,b)” is notation. The other side is the definition of this set.

The definition is the way it is because it works; that’s really all we care about. In fact, we forget about the definition pretty much as soon as we can, and simply use the (a,b) and the “defining property.” We can do that, because we know that “under the hood” there actually is an engine that does what we need it to do, even if we don’t see it working while we are driving the car.

So, there is only one bit of notation, and it's “(a,b)”. The other side is the definition of what that notation actually is.
(Arturo Magidin at math.stackexchange.com)

]

 

 

Source (of text and images):

Wikibooks. “Set Theory/Axioms.” <https://en.wikibooks.org/wiki/Set_Theory/Relations>
(Accessed 27-03-2016)

 

Or if otherwise noted:

Arturo Magidin  at

http://math.stackexchange.com/questions/62908/how-can-an-ordered-pair-be-expressed-as-a-set

 

 

.