summary by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Entry Directory for this Article]
[The following is summary. My own comments and citations are placed in double brackets. All boldface and underlying are mine.]
Mikhail G. Katz and David Sherry
“Leibniz’s Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond”
4. Cum Prodiisset
4.6 Assignable Versus Unassignable
Brief Summary:
In Cum Prodiisset Leibniz works with assignable (finite) and unassignable (infinitesimal / infinite) values. On account of his law of continuity, we can use the same mathematical operations even when we substitute one for the others.
Summary
Leibniz’ infinitesimal values dx and dy are ‘unassignable,’ and Leibniz writes that
the unassignables dx and dy may be substituted for them by a method of supposition even in the case when they are evanescent (Child [Leibniz] 1920, p. 153).
[KS 583]
KS will examine Leibniz’ multiplicative example:
ay = xv
[We will look briefly at Leibniz’ procedures to follow Katz and Sherry. Leibniz writes: “Let ay = xv, then a(d)y = x(d)v + v(d)x.” Leibniz then adds to their corresponding values dy, dx, and dv:
Proof. ay + ady = (x + dx) (v+ dv) “
then expanding
= xv + xdv + vdx +dxdv.
And so together:
ay + ady = (x + dx) (v+ dv) = xv + xdv + vdx +dxdv
or
ay + ady = xv + xdv + vdx +dxdv
(note: there is a transcription error in the translation. In the following, the original has ‘xv’ but the translation has instead ‘xy’.)
We then remove ay and xy (perhaps because they are repeated now in their infinitesimal renditions)
ady = xdv + vdx + dxdv
(then dividing both sides by dx)
This is the formulation KS move next to.]
“Simplifying the differential quotient, Leibniz obtains”
[It seems then that Leibniz will replace the infinitesimals dy and dx with finite differences (d)y and d(x), but he will not do the same for the second d(v) for some reason, leaving it as infinitesimal. Returning to KS:]
At this point Leibniz proposes to transfer ‘‘the matter, as we may, to straight lines that never become evanescent’’, obtaining
KS explain that (d)y and (d)x are assignable, while dv is ‘superfluous’ as ‘it alone can be evanescent’ [KS 583, quoting Leibniz].
[This means that dv can be treated as zero and removed from the equation. Then, we multiple both sides by (d)x to obtain:
Then Leibniz divides both sides by a and by (d)x to obtain:
Then Leibniz notes that (d)y / (d)x “always” equals dy/dx. Thus we can substitute them. This is an application of the principle of continuity again:
Also, since (dy) : (d)x always = dy : dx, it will be allowable to suppose this is true in the case when dy, dx become evanescent, and to say that dy : dx = x + v : a, or ady = xdv + vdx.
(Leibniz 154)
(above by multiplying both sides by a and dx).]
But the law of homogeneity is not mentioned here in Cum Prodiisset, so we do not here have sufficient rational for that step in the operation.
The authors then show a case in the Leibniz text of division by second differentials, which they say is incompatible with the nilsquare approach. [The author’s mention the nilsquare approach in section 4.1]
Bibliography:
Katz, M.; Sherry, D. Leibniz's Infinitesimals: Their Fictionality, Their Modern Implementations, And Their Foes From Berkeley To Russell And Beyond. Erkenntnis 78 (2013), no. 3, 571-625. See http://dx.doi.org/10.1007/s10670-012-9370-y, http://www.ams.org/mathscinet-getitem?mr=3053644, and http://arxiv.org/abs/1205.0174
The above bibliography material taken from the following source, a page by Mikhail Katz, which links to many other recent publications on infinitesimals.
http://u.cs.biu.ac.il/~katzmik/infinitesimals.html
Regarding the Leibniz text:
English references from:
Leibniz. The Early Mathematical Manuscripts of Leibniz. Trans. J.M. Child. Mineola, NY: Dover, 2005 [1920 Open Court].
1920 Edition available at archive.org:
https://archive.org/details/earlymathematic01gerhgoog
Latin references from:
Leibniz. Historia et origo calculi differentialis. Ed. C.I. Gerhardt. Hannover: Im Verlage der Hahn'schen Hofbuchhandlung, 1846]
Available at archive.org:
https://archive.org/details/historiaetorigo00gerhgoog










































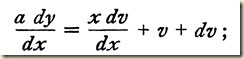


No comments:
Post a Comment