by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Mathematics, Calculus, Geometry, Entry Directory]
[Archimedes, Quadrature of the Parabola, Entry Directory]
Archimedes
Quadrature of the Parabola
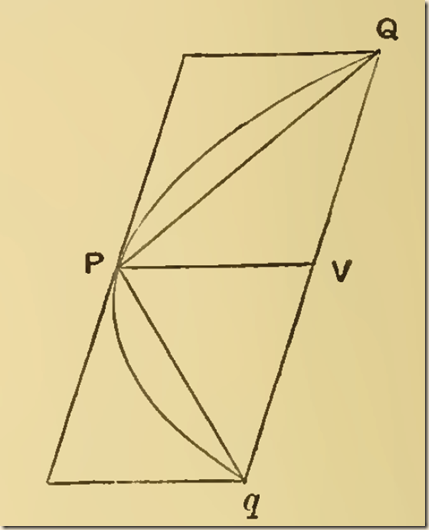
Proposition 20 [quoting]
Proposition 20.
P20. If Qq be the base, and P the vertex, of a parabolic segment, then the triangle PQq is greater than half the segment PQq.
For the chord Qq is parallel to the tangent at P, and the triangle PQq is half the parallelogram formed by Qq, the tangent at P, and the diameters through Q,q. Therefore the triangle PQq is greater than half the segment.
Proposition 20. Corollary
Cor. It follows that it is possible to inscribe in the segment a polygon such that the segments left over are together less than any assigned area.
Archimedes. “Quadrature of the Parabola.” In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at
https://archive.org/details/worksofarchimede00arch





.jpeg)




































No comments:
Post a Comment