by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Mathematics, Calculus, Geometry, Entry Directory]
[Archimedes, Quadrature of the Parabola, Entry Directory]
Archimedes
Quadrature of the Parabola
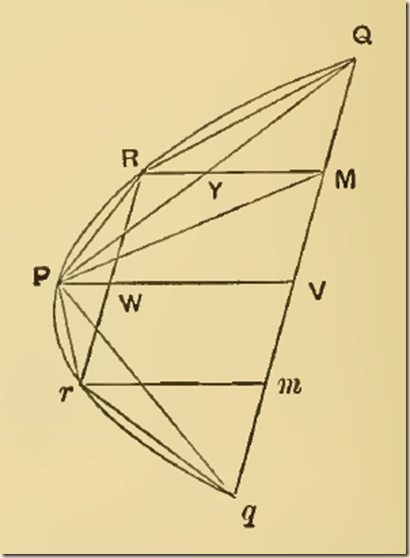
Proposition 21 [quoting]
Proposition 21.
P21. If Qq be the base, and P the vertex, of any parabolic segment, and if R be the vertex of the segment cut off by PQ, then
ΔPQq = 8ΔPRQ.
The diameter through R will bisect the chord PQ, and therefore also QV, where PF is the diameter bisecting Qq. Let the diameter through R bisect PQ in Y and QVinM. Join P3I. By Prop. 19,
Also, if RW, the ordinate from R to PV, be produced to meet the curve again in r,
RW = rW,
and the same proof shows that
ΔPQq = 8ΔPRQ.
Archimedes. “Quadrature of the Parabola.” In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at
https://archive.org/details/worksofarchimede00arch





.jpeg)




































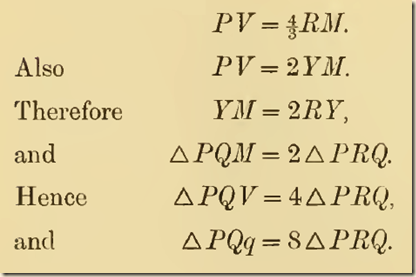
No comments:
Post a Comment