by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Central Entry Directory]
[Mathematics, Calculus, Geometry, Entry Directory]
[Archimedes, Quadrature of the Parabola, Entry Directory]
Archimedes
Quadrature of the Parabola
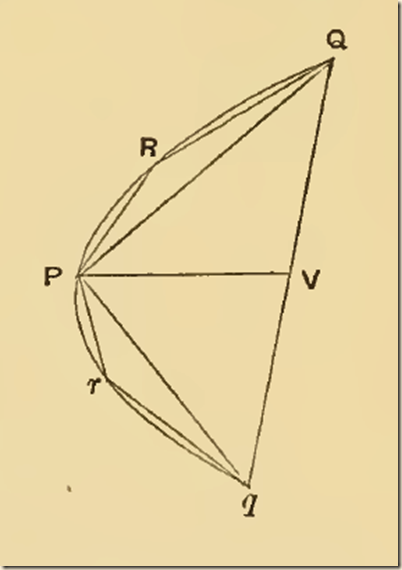
Proposition 22 [quoting]
Proposition 22.
P22. If there he a series of areas A, B, G, D, ... each of which is four times the next in order, and if the largest, A, be equal to the triangle PQq inscribed in a parabolic segment PQq and having the same base with it and equal height, then
(A + B + C + D + ...) < (area of segment PQq).
For, since ΔPQq = 8ΔPRQ = 8Pqr, where R, r are the vertices of the segments cut off by PQ, Pq, as in the last proposition,
ΔPQq = 4 (ΔPQE + ΔPqr).
Therefore, since ΔPQq = A,
ΔPQR + ΔPqr = B.
In like manner we prove that the triangles similarly inscribed in the remaining segments are together equal to the area C, and so on.
Therefore A + B + C+ D + ... is equal to the area of a certain inscribed polygon, and is therefore less than the area of the segment.
Archimedes. “Quadrature of the Parabola.” In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at
https://archive.org/details/worksofarchimede00arch





.jpeg)




































No comments:
Post a Comment