Archimedes’ “On the Equilibrium of Planes”, Prop 9

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]

[Mathematics, Calculus, Geometry, Entry Directory]

[Archimedes Entry Directory]

[“On the Equilibrium of Planes”, Entry Directory]

 

Archimedes

On the Equilibrium of Planes

or

The Centres of Gravity of Planes,

Book I

Proposition 9

[The following is quotation]

 

Proposition 9 

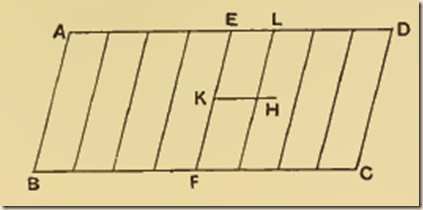
P9. The centre of gravity of any parallelogram lies on the straight line joining the middle pints of opposite sides.

Let ABCD be a parallelogram, and let EF join the middle points of the opposite sides AD, BC.

If the centre of gravity does not lie on EF, suppose it to be H, and draw HK parallel to AD or BC meeting EF in K.

(Heath 194)

Then it is possible, by bisecting ED, then bisecting the halves, and so on continually, to arrive at a length EL less

than KH. Divide both AE and ED into parts each equal to EL, and through the points of division draw parallels to AB or CD.

We have then a number of equal and similar parallelograms, and, if any one be applied to any other, their centres of gravity coincide [Post. 4]. Thus we have an even number of equal magnitudes whose centres of gravity lie at equal distances along a straight line. Hence the centre of gravity of the whole parallelogram will lie on the line joining the centres of gravity of the two middle parallelograms [Prop. 5, Cor. 2].

But this is impossible, for H is outside the middle parallelograms.

Therefore the centre of gravity cannot but lie on EF.

 

From:

Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at

https://archive.org/details/worksofarchimede00arch