by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]
[Mathematics, Calculus, Geometry, Entry Directory]
[“On the Equilibrium of Planes”, Entry Directory]
Archimedes
On the Equilibrium of Planes
or
The Centres of Gravity of Planes,
Book I
Proposition 15
[The following is quotation]
Proposition 15
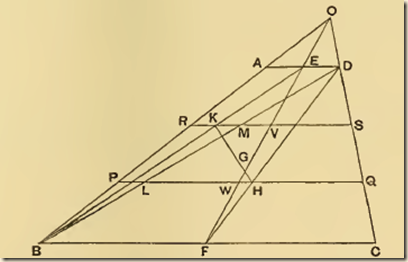
P15. If AD, BC he the two parallel sides of a trapezium ABCD, AD being the smaller, and if AD, BC be bisected at E, F respectively, then the centre of gravity of the trapezium is at a point G on EF such that
GE : GF = (2BC + AD) : (2AD + BC).
Produce BA, CD to meet at O. Then FE produced will also pass through 0, since AE = ED, and BF = FC.
Now the centre of gravity of the triangle OAD will lie on OE, and that of the triangle OBC will lie on OF. [Prop. 13]
It follows that the centre of gravity of the remainder, the trapezium ABCD, will also lie on OF. [Prop. 8]
Join BD, and divide it at L, M into three equal parts. Through L, M draw PQ, RS parallel to BC meeting BA in P, R, FE in W, V, and CD in Q, S respectively.
Join DF, BE meeting PQ in H and RS in K respectively.
Now, since
BL = 1/3BD,
FH=1/3FD.
(Heath 201)
Therefore H is the centre of gravity of the triangle DBC*. [* This easy deduction from Prop. 14 is assumed by Archimedes without proof.]
Similarly, since EK = 1/3BE, it follows that K is the centre of gravity of the triangle ADB.
Therefore the centre of gravity of the triangles DBC, ADB together, i.e. of the trapezium, lies on the line HK.
But it also lies on OF.
Therefore, if OF, HK meet in G, G is the centre of gravity of the trapezium.
Hence [Props. 6, 7]
ΔDBC : ΔABD = KG : GH
= VG: GW.
But ΔDBC : ΔABD = BC: AD.
Therefore BC : AD = VG : GW.
It follows that (2BC + AD) : (2AD + BC) = (2VG + GW) : (2GW + VG) = EG : GF.
Q. E. D.
(Heath 202)
From:
Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at
https://archive.org/details/worksofarchimede00arch





.jpeg)




































No comments:
Post a Comment