Archimedes’ “On the Equilibrium of Planes”, Prop 13

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

 

[Central Entry Directory]

[Mathematics, Calculus, Geometry, Entry Directory]

[Archimedes Entry Directory]

[“On the Equilibrium of Planes”, Entry Directory]

 

Archimedes

On the Equilibrium of Planes

or

The Centres of Gravity of Planes,

Book I

Proposition 13

[The following is quotation]

 

Proposition 13

P13. In any triangle the centre of gravity lies on the straight line joining any angle to the oniddle point of the opposite side.

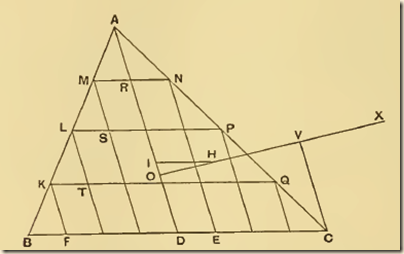
Let ABC be a triangle and D the middle point of BC. Join AD. Then shall the centre of gravity lie on AD.

For, if possible, let this not be the case, and let H be the centre of gravity. Draw HI parallel to CB meeting AD in I.

Then, if we bisect DC, then bisect the halves, and so on, we shall at length arrive at a length, as DE, less than HI.

Divide both BD and DC into lengths each equal to DE, and through the points of division draw lines each parallel to DA meeting BA and AC in points as K, L, M and N, P, Q respectively.

Join MN, LP, KQ, which lines will then be each parallel to BC.

We have now a series of parallelograms as FQ, TP, SN, and AD bisects opposite sides in each. Thus the centre of gravity of each parallelogram lies on AD [Prop. 9], and therefore the centre of gravity of the figure made up of them all lies on AD.

(Heath 198)

Let the centre of gravity of all the parallelograms taken together be O. Join OH and produce it; also draw CV parallel to DA meeting OH produced in V.

Now, if n be the number of parts into which AC is divided,

ΔADC : (sum of triangles on AN, NP, ...)

= AC² : (AN² + NP² + ... )

= n² : n

= n : 1

= AC : AN.

Similarly

ΔABD : (sum of triangles on AM, ML, ...) = AB : AM.

And

AG : AN = AB : AM.

It follows that

ΔABC : (sum of all the small Δs) = CA : AN

> VO : OH, by parallels.

Suppose OV produced to X so that

ΔABC: (sum of small Δs) = XO : OH,

whence, dividendo,

(sum of parallelograms) : (sum of small Δs) = XH : HO.

Since then the centre of gravity of the triangle ABC is at H, and the centre of gravity of the part of it made up of the parallelograms is at O, it follows from Prop. 8 that the centre of gravity of the remaining portion consisting of all the small triangles taken together is at X. But this is impossible, since all the triangles are on one side of the line through X parallel to AD.

Therefore the centre of gravity of the triangle cannot but lie on AD.

Alternative proof.

Suppose, if possible, that H, not lying on AD, is the centre of gravity of the triangle ABC. Join AH, BH, CH. Let E, F be the middle points of CA, AB respectively, and join DE, EF, FD. Let EF meet AD in M.

(Heath 199)

Draw FK, EL parallel to AH meeting BH, CH in K, L respectively. Join KD, HD, LD, KL. Let KL meet DH in N, and join MN.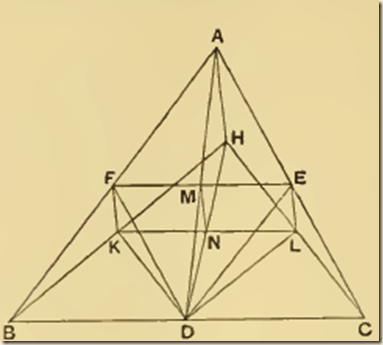

Since DE is parallel to AB, the triangles ABC, EDC are similar. And, since CE = EA, and EL is parallel to AH, it follows that CL = LH And CD = DB. Therefore BH is parallel to DL.

Thus in the similar and similarly situated triangles ABC, EDC the straight lines AH, BH are respectively parallel to EL, DL; and it follows that H, L are similarly situated with respect to the triangles respectively.

But H is, by hypothesis, the centre of gravity of ABC. Therefore L is the centre of gravity of EDC. [Prop. 11]

Similarly the point K is the centre of gravity of the triangle FBD.

And the triangles FBD, EDC are equal, so that the centre of gravity of both together is at the middle point of KL, i.e. at the point N.

The remainder of the triangle ABC, after the triangles FBD, EDC are deducted, is the parallelogram AFDE, and the centre of gravity of this parallelogram is at M, the intersection of its diagonals.

It follows that the centre of gravity of the whole triangle ABC must lie on MN; that is, MN must pass through H, which is impossible (since MN is parallel to AH).

Therefore the centre of gravity of the triangle ABC cannot but lie on AD.

(Heath 200)

From:

Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at

https://archive.org/details/worksofarchimede00arch