Archimedes’ “On the Equilibrium of Planes”, Prop 6, 7

 

by Corry Shores
[Search Blog Here. Index-tags are found on the bottom of the left column.]

[Central Entry Directory]

[Mathematics, Calculus, Geometry, Entry Directory]

[Archimedes Entry Directory]

[“On the Equilibrium of Planes”, Entry Directory]

 

Archimedes

On the Equilibrium of Planes

or

The Centres of Gravity of Planes,

Book I

Proposition 6, 7

[The following is quotation]

 

 

 

Propositions 6, 7.

P6, 7. Two magnitudes, whether commensurable [Prop. 6] or incommensurable [Prop. 7], balance at distances reciprocally proportional to the magnitudes.

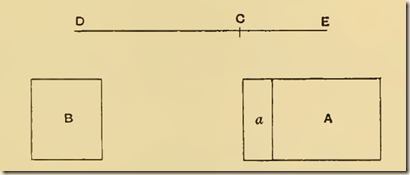
I. Suppose the magnitudes A, B to be commensurable, and the points A, B to be their centres of gravity. Let DE be a straight line so divided at C that

A : B = DC : CE.

We have then to prove that, if A be placed at E and B at D, C is the centre of gravity of the two taken together.

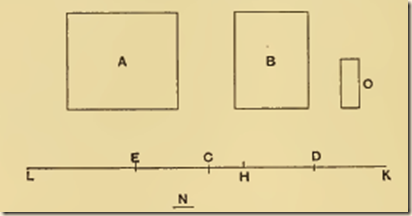
Since A, B are commensurable, so are DC, CE. Let N be a common measure of DC, CE. Make DH, DK each equal to CE, and EL (on CE produced) equal to CD. Then EH= CD, since DH = CE. Therefore LH is bisected at E, as HK is bisected at D.

Thus LH, HK must each contain N an even number of times.

Take a magnitude O such that O is contained as many times in A as N is contained in LH, whence

A : O = LH : N.

But

B : A = CE : DC

= HK : LH.

Hence, ex aequali, B : O = HK : N, or O is contained in B as many times as N is contained in HK.

Thus O is a common measure of A, B.

(Heath 192)

Divide LH, HK into parts each equal to N, and A, B into parts each equal to O. The parts of A will therefore be equal in number to those of LH, and the parts of B equal in number to those of HK. Place one of the parts of A at the middle point of each of the parts N of LH, and one of the parts of B at the middle point of each of the parts N of HK.

Then the centre of gravity of the parts of A placed at equal distances on LH will be at E, the middle point of LH [Prop. 5, Cor. 2], and the centre of gravity of the parts of B placed at equal distances along HK will be at D, the middle point of HK.

Thus we may suppose A itself applied at E, and B itself applied at D.

But the system formed by the parts O of A and B together is a system of equal magnitudes even in number and placed at equal distances along LK. And, since LE = CD, and EG = DK, LC = CK, so that C is the middle point of LK. Therefore G is the centre of gravity of the system ranged along LK.

Therefore A acting at E and B acting at D balance about the point C.

 

II. Suppose the magnitudes to be incommensurable, and let them be (A + a) and B respectively. Let DE be a line divided at C so that

(A + a) : B = DC : CE.

Then, if (A + a) placed at E and B placed at D do not balance about C, (A + a) is either too great to balance B, or not great enough.

Suppose, if possible, that (A + a) is too great to balance B. Take from (A + a) a magnitude a smaller than the deduction which would make the remainder balance B, but such that the remainder A and the magnitude B are commensurable.

(Heath 193)

Then, since A, B are commensurable, and

A  B < DC : CE,

A and B will not balance [Prop. 6], but D will be depressed. But this is impossible, since the deduction a was an insufficient deduction from (A + a) to produce equilibrium, so that E was still depressed.

Therefore (A + a) is not too great to balance B; and similarly it may be proved that B is not too great to balance (A + a).

Hence (A + a), B taken together have their centre of gravity at C.

From:

Archimedes. “On the Equilibrium of Planes or The Centres of Gravity of Planes, Book I”. In The Works of Archimedes. Ed. T.L. Heath. Cambridge UP, 1897. Obtained at

https://archive.org/details/worksofarchimede00arch